predict
Class: RegressionLinear
Predict response of linear regression model
Description
YHat = predict(Mdl,X,Name,Value)
Input Arguments
Linear regression model, specified as a RegressionLinear model
object. You can create a RegressionLinear model
object using fitrlinear.
Predictor data used to generate responses, specified as a full or sparse numeric matrix or a table.
By default, each row of X corresponds to one
observation, and each column corresponds to one variable.
For a numeric matrix:
The variables in the columns of
Xmust have the same order as the predictor variables that trainedMdl.If you train
Mdlusing a table (for example,Tbl) andTblcontains only numeric predictor variables, thenXcan be a numeric matrix. To treat numeric predictors inTblas categorical during training, identify categorical predictors by using theCategoricalPredictorsname-value pair argument offitrlinear. IfTblcontains heterogeneous predictor variables (for example, numeric and categorical data types) andXis a numeric matrix, thenpredictthrows an error.
For a table:
predictdoes not support multicolumn variables or cell arrays other than cell arrays of character vectors.If you train
Mdlusing a table (for example,Tbl), then all predictor variables inXmust have the same variable names and data types as the variables that trainedMdl(stored inMdl.PredictorNames). However, the column order ofXdoes not need to correspond to the column order ofTbl. Also,TblandXcan contain additional variables (response variables, observation weights, and so on), butpredictignores them.If you train
Mdlusing a numeric matrix, then the predictor names inMdl.PredictorNamesmust be the same as the corresponding predictor variable names inX. To specify predictor names during training, use thePredictorNamesname-value pair argument offitrlinear. All predictor variables inXmust be numeric vectors.Xcan contain additional variables (response variables, observation weights, and so on), butpredictignores them.
Note
If you orient your predictor matrix so that observations correspond to
columns and specify "ObservationsIn","columns", then
you might experience a significant reduction in optimization execution
time. You cannot specify "ObservationsIn","columns"
for predictor data in a table.
Data Types: double | single | table
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: predict(Mdl,X,"ObservationsIn","columns") indicates
that columns in the predictor data correspond to observations.
Predictor data observation dimension, specified as
"columns" or "rows".
Note
If you orient your predictor matrix so that observations
correspond to columns and specify
"ObservationsIn","columns", then you might
experience a significant reduction in optimization execution time.
You cannot specify "ObservationsIn","columns" for
predictor data in a table.
Data Types: char | string
Since R2023b
Predicted response value to use for observations with missing predictor values, specified as "median", "mean", or a numeric scalar.
| Value | Description |
|---|---|
"median" | predict uses the median of the observed response values in the training data as the predicted response value for observations with missing predictor values. |
"mean" | predict uses the mean of the observed response values in the training data as the predicted response value for observations with missing predictor values. |
| Numeric scalar | predict uses this value as the predicted response value for observations with missing predictor values. |
Example: PredictionForMissingValue="mean"
Example: PredictionForMissingValue=NaN
Data Types: single | double | char | string
Output Arguments
Predicted responses, returned as a n-by-L numeric
matrix. n is the number of observations in X and L is
the number of regularization strengths in Mdl.Lambda. YHat( is
the response for observation i,j)i using the
linear regression model that has regularization strength Mdl.Lambda(.j)
The predicted response using the model with regularization strength j is
x is an observation from the predictor data matrix
X, and is row vector.is the estimated column vector of coefficients. The software stores this vector in
Mdl.Beta(:,.j)is the estimated, scalar bias, which the software stores in
Mdl.Bias(.j)
Examples
Simulate 10000 observations from this model
is a 10000-by-1000 sparse matrix with 10% nonzero standard normal elements.
e is random normal error with mean 0 and standard deviation 0.3.
rng(1) % For reproducibility
n = 1e4;
d = 1e3;
nz = 0.1;
X = sprandn(n,d,nz);
Y = X(:,100) + 2*X(:,200) + 0.3*randn(n,1);Train a linear regression model. Reserve 30% of the observations as a holdout sample.
CVMdl = fitrlinear(X,Y,'Holdout',0.3);
Mdl = CVMdl.Trained{1}Mdl =
RegressionLinear
ResponseName: 'Y'
ResponseTransform: 'none'
Beta: [1000×1 double]
Bias: -0.0066
Lambda: 1.4286e-04
Learner: 'svm'
Properties, Methods
CVMdl is a RegressionPartitionedLinear model. It contains the property Trained, which is a 1-by-1 cell array holding a RegressionLinear model that the software trained using the training set.
Extract the training and test data from the partition definition.
trainIdx = training(CVMdl.Partition); testIdx = test(CVMdl.Partition);
Predict the training- and test-sample responses.
yHatTrain = predict(Mdl,X(trainIdx,:)); yHatTest = predict(Mdl,X(testIdx,:));
Because there is one regularization strength in Mdl, yHatTrain and yHatTest are numeric vectors.
Predict responses from the best-performing, linear regression model that uses a lasso-penalty and least squares.
Simulate 10000 observations as in Predict Test-Sample Responses.
rng(1) % For reproducibility
n = 1e4;
d = 1e3;
nz = 0.1;
X = sprandn(n,d,nz);
Y = X(:,100) + 2*X(:,200) + 0.3*randn(n,1);Create a set of 15 logarithmically-spaced regularization strengths from through .
Lambda = logspace(-5,-1,15);
Cross-validate the models. To increase execution speed, transpose the predictor data and specify that the observations are in columns. Optimize the objective function using SpaRSA.
X = X'; CVMdl = fitrlinear(X,Y,'ObservationsIn','columns','KFold',5,'Lambda',Lambda,... 'Learner','leastsquares','Solver','sparsa','Regularization','lasso'); numCLModels = numel(CVMdl.Trained)
numCLModels = 5
CVMdl is a RegressionPartitionedLinear model. Because fitrlinear implements 5-fold cross-validation, CVMdl contains 5 RegressionLinear models that the software trains on each fold.
Display the first trained linear regression model.
Mdl1 = CVMdl.Trained{1}Mdl1 =
RegressionLinear
ResponseName: 'Y'
ResponseTransform: 'none'
Beta: [1000×15 double]
Bias: [-0.0049 -0.0049 -0.0049 -0.0049 -0.0049 -0.0048 -0.0044 -0.0037 -0.0030 -0.0031 -0.0033 -0.0036 -0.0041 -0.0051 -0.0071]
Lambda: [1.0000e-05 1.9307e-05 3.7276e-05 7.1969e-05 1.3895e-04 2.6827e-04 5.1795e-04 1.0000e-03 0.0019 0.0037 0.0072 0.0139 0.0268 0.0518 0.1000]
Learner: 'leastsquares'
Properties, Methods
Mdl1 is a RegressionLinear model object. fitrlinear constructed Mdl1 by training on the first four folds. Because Lambda is a sequence of regularization strengths, you can think of Mdl1 as 11 models, one for each regularization strength in Lambda.
Estimate the cross-validated MSE.
mse = kfoldLoss(CVMdl);
Higher values of Lambda lead to predictor variable sparsity, which is a good quality of a regression model. For each regularization strength, train a linear regression model using the entire data set and the same options as when you cross-validated the models. Determine the number of nonzero coefficients per model.
Mdl = fitrlinear(X,Y,'ObservationsIn','columns','Lambda',Lambda,... 'Learner','leastsquares','Solver','sparsa','Regularization','lasso'); numNZCoeff = sum(Mdl.Beta~=0);
In the same figure, plot the cross-validated MSE and frequency of nonzero coefficients for each regularization strength. Plot all variables on the log scale.
figure; [h,hL1,hL2] = plotyy(log10(Lambda),log10(mse),... log10(Lambda),log10(numNZCoeff)); hL1.Marker = 'o'; hL2.Marker = 'o'; ylabel(h(1),'log_{10} MSE') ylabel(h(2),'log_{10} nonzero-coefficient frequency') xlabel('log_{10} Lambda') hold off
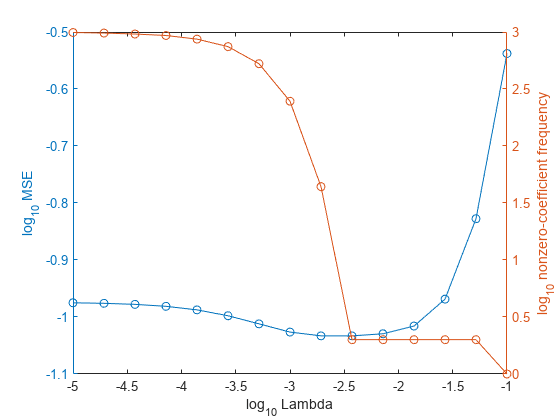
Choose the index of the regularization strength that balances predictor variable sparsity and low MSE (for example, Lambda(10)).
idxFinal = 10;
Extract the model with corresponding to the minimal MSE.
MdlFinal = selectModels(Mdl,idxFinal)
MdlFinal =
RegressionLinear
ResponseName: 'Y'
ResponseTransform: 'none'
Beta: [1000×1 double]
Bias: -0.0050
Lambda: 0.0037
Learner: 'leastsquares'
Properties, Methods
idxNZCoeff = find(MdlFinal.Beta~=0)
idxNZCoeff = 2×1
100
200
EstCoeff = Mdl.Beta(idxNZCoeff)
EstCoeff = 2×1
1.0051
1.9965
MdlFinal is a RegressionLinear model with one regularization strength. The nonzero coefficients EstCoeff are close to the coefficients that simulated the data.
Simulate 10 new observations, and predict corresponding responses using the best-performing model.
XNew = sprandn(d,10,nz); YHat = predict(MdlFinal,XNew,'ObservationsIn','columns');
Alternative Functionality
Simulink Block
To integrate the prediction of a linear regression model into Simulink®, you can use the RegressionLinear
Predict block in the Statistics and Machine Learning Toolbox™ library or a MATLAB® Function block with the predict function. For
examples, see Predict Responses Using RegressionLinear Predict Block and Predict Class Labels Using MATLAB Function Block.
When deciding which approach to use, consider the following:
If you use the Statistics and Machine Learning Toolbox library block, you can use the Fixed-Point Tool (Fixed-Point Designer) to convert a floating-point model to fixed point.
Support for variable-size arrays must be enabled for a MATLAB Function block with the
predictfunction.If you use a MATLAB Function block, you can use MATLAB functions for preprocessing or post-processing before or after predictions in the same MATLAB Function block.
Extended Capabilities
The
predict function supports tall arrays with the following usage
notes and limitations:
predictdoes not support talltabledata.
For more information, see Tall Arrays.
Usage notes and limitations:
You can generate C/C++ code for both
predictandupdateby using a coder configurer. Or, generate code only forpredictby usingsaveLearnerForCoder,loadLearnerForCoder, andcodegen.Code generation for
predictandupdate— Create a coder configurer by usinglearnerCoderConfigurerand then generate code by usinggenerateCode. Then you can update model parameters in the generated code without having to regenerate the code.Code generation for
predict— Save a trained model by usingsaveLearnerForCoder. Define an entry-point function that loads the saved model by usingloadLearnerForCoderand calls thepredictfunction. Then usecodegen(MATLAB Coder) to generate code for the entry-point function.
To generate single-precision C/C++ code for
predict, specifyDataType="single"when you call theloadLearnerForCoderfunction.This table contains notes about the arguments of
predict. Arguments not included in this table are fully supported.Argument Notes and Limitations MdlFor the usage notes and limitations of the model object, see Code Generation of the
RegressionLinearobject.XFor general code generation,
Xmust be a single-precision or double-precision matrix or a table containing numeric variables, categorical variables, or both.In the coder configurer workflow,
Xmust be a single-precision or double-precision matrix.The number of observations in
Xcan be a variable size, but the number of variables inXmust be fixed.If you want to specify
Xas a table, then your model must be trained using a table, and your entry-point function for prediction must do the following:Accept data as arrays.
Create a table from the data input arguments and specify the variable names in the table.
Pass the table to
predict.
For an example of this table workflow, see Generate Code to Classify Data in Table. For more information on using tables in code generation, see Code Generation for Tables (MATLAB Coder) and Table Limitations for Code Generation (MATLAB Coder).
Name-value arguments Names in name-value arguments must be compile-time constants.
The
ObservationsInvalue must be a compile-time constant. For example, to use"ObservationsIn","columns"in the generated code, include{coder.Constant("ObservationsIn"),coder.Constant("columns")}in the-argsvalue ofcodegen(MATLAB Coder).If the value of
PredictionForMissingValueis nonnumeric, then it must be a compile-time constant.
For more information, see Introduction to Code Generation.
This function fully supports GPU arrays. For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Version History
Introduced in R2016aStarting in R2024a, predict accepts GPU array input
arguments with some limitations.
Starting in R2023b, when you predict or compute the loss, some regression models allow you to specify the predicted response value for observations with missing predictor values. Specify the PredictionForMissingValue name-value argument to use a numeric scalar, the training set median, or the training set mean as the predicted value. When computing the loss, you can also specify to omit observations with missing predictor values.
This table lists the object functions that support the
PredictionForMissingValue name-value argument. By default, the
functions use the training set median as the predicted response value for observations with
missing predictor values.
| Model Type | Model Objects | Object Functions |
|---|---|---|
| Gaussian process regression (GPR) model | RegressionGP, CompactRegressionGP | loss, predict, resubLoss, resubPredict |
RegressionPartitionedGP | kfoldLoss, kfoldPredict | |
| Gaussian kernel regression model | RegressionKernel | loss, predict |
RegressionPartitionedKernel | kfoldLoss, kfoldPredict | |
| Linear regression model | RegressionLinear | loss, predict |
RegressionPartitionedLinear | kfoldLoss, kfoldPredict | |
| Neural network regression model | RegressionNeuralNetwork, CompactRegressionNeuralNetwork | loss, predict, resubLoss, resubPredict |
RegressionPartitionedNeuralNetwork | kfoldLoss, kfoldPredict | |
| Support vector machine (SVM) regression model | RegressionSVM, CompactRegressionSVM | loss, predict, resubLoss, resubPredict |
RegressionPartitionedSVM | kfoldLoss, kfoldPredict |
In previous releases, the regression model loss and predict functions listed above used NaN predicted response values for observations with missing predictor values. The software omitted observations with missing predictor values from the resubstitution ("resub") and cross-validation ("kfold") computations for prediction and loss.
See Also
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)