fitrlinear
Fit linear regression model to high-dimensional data
Syntax
Description
fitrlinear efficiently trains linear regression models with high-dimensional, full or sparse predictor data. Available linear regression models include regularized support vector machines (SVM) and least-squares regression methods. fitrlinear minimizes the objective function using techniques that reduce computing time (e.g., stochastic gradient descent).
For reduced computation time on a high-dimensional data set that includes many predictor variables, train a linear regression model by using fitrlinear. For low- through medium-dimensional predictor data sets, see Alternatives for Lower-Dimensional Data.
Mdl = fitrlinear(Tbl,ResponseVarName)Tbl and the response values in Tbl.ResponseVarName.
Mdl = fitrlinear(X,Y,Name,Value)'Kfold' name-value pair argument. The cross-validation results determine how well the model generalizes.
[
also returns the hyperparameter optimization results when you specify
Mdl,FitInfo,HyperparameterOptimizationResults] = fitrlinear(___)OptimizeHyperparameters.
[
also returns Mdl,FitInfo,AggregateOptimizationResults] = fitrlinear(___)AggregateOptimizationResults, which contains
hyperparameter optimization results when you specify the
OptimizeHyperparameters and
HyperparameterOptimizationOptions name-value arguments.
You must also specify the ConstraintType and
ConstraintBounds options of
HyperparameterOptimizationOptions. You can use this
syntax to optimize on compact model size instead of cross-validation loss, and
to perform a set of multiple optimization problems that have the same options
but different constraint bounds.
Examples
Train a linear regression model using SVM, dual SGD, and ridge regularization.
Simulate 10000 observations from this model
is a 10000-by-1000 sparse matrix with 10% nonzero standard normal elements.
e is random normal error with mean 0 and standard deviation 0.3.
rng(1) % For reproducibility
n = 1e4;
d = 1e3;
nz = 0.1;
X = sprandn(n,d,nz);
Y = X(:,100) + 2*X(:,200) + 0.3*randn(n,1);Train a linear regression model. By default, fitrlinear uses support vector machines with a ridge penalty, and optimizes using dual SGD for SVM. Determine how well the optimization algorithm fit the model to the data by extracting a fit summary.
[Mdl,FitInfo] = fitrlinear(X,Y)
Mdl =
RegressionLinear
ResponseName: 'Y'
ResponseTransform: 'none'
Beta: [1000×1 double]
Bias: -0.0056
Lambda: 1.0000e-04
Learner: 'svm'
Properties, Methods
FitInfo = struct with fields:
Lambda: 1.0000e-04
Objective: 0.2725
PassLimit: 10
NumPasses: 10
BatchLimit: []
NumIterations: 100000
GradientNorm: NaN
GradientTolerance: 0
RelativeChangeInBeta: 0.4907
BetaTolerance: 1.0000e-04
DeltaGradient: 1.5816
DeltaGradientTolerance: 0.1000
TerminationCode: 0
TerminationStatus: {'Iteration limit exceeded.'}
Alpha: [10000×1 double]
History: []
FitTime: 0.0585
Solver: {'dual'}
Mdl is a RegressionLinear model. You can pass Mdl and the training or new data to loss to inspect the in-sample mean-squared error. Or, you can pass Mdl and new predictor data to predict to predict responses for new observations.
FitInfo is a structure array containing, among other things, the termination status (TerminationStatus) and how long the solver took to fit the model to the data (FitTime). It is good practice to use FitInfo to determine whether optimization-termination measurements are satisfactory. In this case, fitrlinear reached the maximum number of iterations. Because training time is fast, you can retrain the model, but increase the number of passes through the data. Or, try another solver, such as LBFGS.
To determine a good lasso-penalty strength for a linear regression model that uses least squares, implement 5-fold cross-validation.
Simulate 10000 observations from this model
is a 10000-by-1000 sparse matrix with 10% nonzero standard normal elements.
e is random normal error with mean 0 and standard deviation 0.3.
rng(1) % For reproducibility
n = 1e4;
d = 1e3;
nz = 0.1;
X = sprandn(n,d,nz);
Y = X(:,100) + 2*X(:,200) + 0.3*randn(n,1);Create a set of 15 logarithmically-spaced regularization strengths from through .
Lambda = logspace(-5,-1,15);
Cross-validate the models. To increase execution speed, transpose the predictor data and specify that the observations are in columns. Optimize the objective function using SpaRSA.
X = X'; CVMdl = fitrlinear(X,Y,'ObservationsIn','columns','KFold',5,'Lambda',Lambda,... 'Learner','leastsquares','Solver','sparsa','Regularization','lasso'); numCLModels = numel(CVMdl.Trained)
numCLModels = 5
CVMdl is a RegressionPartitionedLinear model. Because fitrlinear implements 5-fold cross-validation, CVMdl contains 5 RegressionLinear models that the software trains on each fold.
Display the first trained linear regression model.
Mdl1 = CVMdl.Trained{1}Mdl1 =
RegressionLinear
ResponseName: 'Y'
ResponseTransform: 'none'
Beta: [1000×15 double]
Bias: [-0.0049 -0.0049 -0.0049 -0.0049 -0.0049 -0.0048 -0.0044 -0.0037 -0.0030 -0.0031 -0.0033 -0.0036 -0.0041 -0.0051 -0.0071]
Lambda: [1.0000e-05 1.9307e-05 3.7276e-05 7.1969e-05 1.3895e-04 2.6827e-04 5.1795e-04 1.0000e-03 0.0019 0.0037 0.0072 0.0139 0.0268 0.0518 0.1000]
Learner: 'leastsquares'
Properties, Methods
Mdl1 is a RegressionLinear model object. fitrlinear constructed Mdl1 by training on the first four folds. Because Lambda is a sequence of regularization strengths, you can think of Mdl1 as 15 models, one for each regularization strength in Lambda.
Estimate the cross-validated MSE.
mse = kfoldLoss(CVMdl);
Higher values of Lambda lead to predictor variable sparsity, which is a good quality of a regression model. For each regularization strength, train a linear regression model using the entire data set and the same options as when you cross-validated the models. Determine the number of nonzero coefficients per model.
Mdl = fitrlinear(X,Y,'ObservationsIn','columns','Lambda',Lambda,... 'Learner','leastsquares','Solver','sparsa','Regularization','lasso'); numNZCoeff = sum(Mdl.Beta~=0);
In the same figure, plot the cross-validated MSE and frequency of nonzero coefficients for each regularization strength. Plot all variables on the log scale.
figure [h,hL1,hL2] = plotyy(log10(Lambda),log10(mse),... log10(Lambda),log10(numNZCoeff)); hL1.Marker = 'o'; hL2.Marker = 'o'; ylabel(h(1),'log_{10} MSE') ylabel(h(2),'log_{10} nonzero-coefficient frequency') xlabel('log_{10} Lambda') hold off
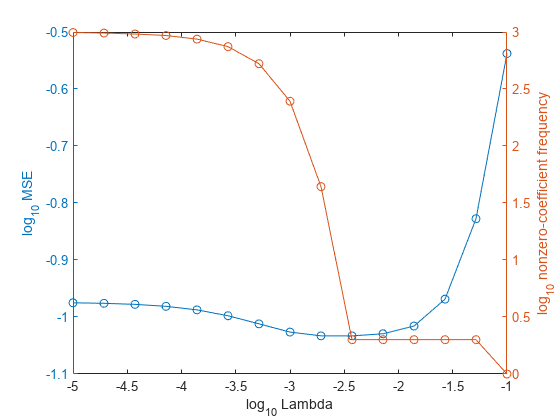
Choose the index of the regularization strength that balances predictor variable sparsity and low MSE (for example, Lambda(10)).
idxFinal = 10;
Extract the model with corresponding to the minimal MSE.
MdlFinal = selectModels(Mdl,idxFinal)
MdlFinal =
RegressionLinear
ResponseName: 'Y'
ResponseTransform: 'none'
Beta: [1000×1 double]
Bias: -0.0050
Lambda: 0.0037
Learner: 'leastsquares'
Properties, Methods
idxNZCoeff = find(MdlFinal.Beta~=0)
idxNZCoeff = 2×1
100
200
EstCoeff = Mdl.Beta(idxNZCoeff)
EstCoeff = 2×1
1.0051
1.9965
MdlFinal is a RegressionLinear model with one regularization strength. The nonzero coefficients EstCoeff are close to the coefficients that simulated the data.
This example shows how to optimize hyperparameters automatically using fitrlinear. The example uses artificial (simulated) data for the model
is a 10000-by-1000 sparse matrix with 10% nonzero standard normal elements.
e is random normal error with mean 0 and standard deviation 0.3.
rng(1) % For reproducibility
n = 1e4;
d = 1e3;
nz = 0.1;
X = sprandn(n,d,nz);
Y = X(:,100) + 2*X(:,200) + 0.3*randn(n,1);Find hyperparameters that minimize five-fold cross validation loss by using automatic hyperparameter optimization.
For reproducibility, use the 'expected-improvement-plus' acquisition function.
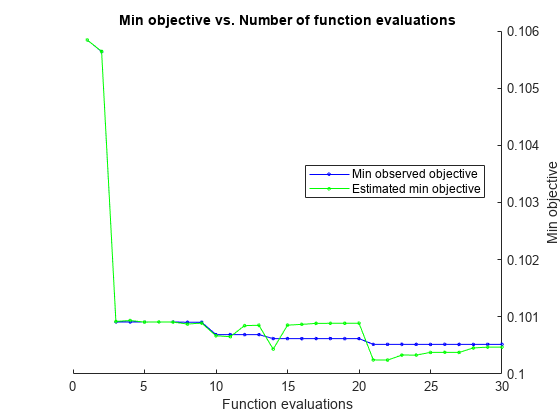
hyperopts = struct('AcquisitionFunctionName','expected-improvement-plus'); [Mdl,FitInfo,HyperparameterOptimizationResults] = fitrlinear(X,Y,... 'OptimizeHyperparameters','auto',... 'HyperparameterOptimizationOptions',hyperopts)
|=====================================================================================================|
| Iter | Eval | Objective: | Objective | BestSoFar | BestSoFar | Lambda | Learner |
| | result | log(1+loss) | runtime | (observed) | (estim.) | | |
|=====================================================================================================|
| 1 | Best | 0.10584 | 1.6226 | 0.10584 | 0.10584 | 2.4206e-09 | svm |
| 2 | Best | 0.10564 | 1.1922 | 0.10564 | 0.10564 | 0.001807 | svm |
| 3 | Best | 0.10091 | 0.42406 | 0.10091 | 0.10092 | 2.4681e-09 | leastsquares |
| 4 | Accept | 0.11397 | 0.3295 | 0.10091 | 0.10094 | 0.021027 | leastsquares |
| 5 | Accept | 0.10091 | 0.38216 | 0.10091 | 0.10091 | 2.0258e-09 | leastsquares |
| 6 | Accept | 0.45312 | 0.5886 | 0.10091 | 0.10091 | 9.8803 | svm |
| 7 | Accept | 0.10582 | 1.2478 | 0.10091 | 0.10091 | 9.6038e-06 | svm |
| 8 | Best | 0.10091 | 0.35743 | 0.10091 | 0.10087 | 1.6009e-05 | leastsquares |
| 9 | Accept | 0.44998 | 0.22218 | 0.10091 | 0.10089 | 9.9615 | leastsquares |
| 10 | Best | 0.10069 | 0.33557 | 0.10069 | 0.10067 | 0.00079258 | leastsquares |
| 11 | Accept | 0.10586 | 1.1482 | 0.10069 | 0.10065 | 9.7512e-08 | svm |
| 12 | Accept | 0.10091 | 0.33462 | 0.10069 | 0.10085 | 3.0897e-07 | leastsquares |
| 13 | Accept | 0.10577 | 1.2609 | 0.10069 | 0.10085 | 0.00019626 | svm |
| 14 | Best | 0.10062 | 0.42974 | 0.10062 | 0.10043 | 0.0037706 | leastsquares |
| 15 | Accept | 0.10091 | 0.39437 | 0.10062 | 0.10085 | 2.4399e-08 | leastsquares |
| 16 | Accept | 0.10091 | 0.3369 | 0.10062 | 0.10087 | 2.4005e-06 | leastsquares |
| 17 | Accept | 0.10091 | 0.32505 | 0.10062 | 0.10089 | 1.0029e-09 | leastsquares |
| 18 | Accept | 0.10584 | 1.1459 | 0.10062 | 0.10089 | 1.0049e-09 | svm |
| 19 | Accept | 0.10088 | 0.33068 | 0.10062 | 0.10089 | 0.00010204 | leastsquares |
| 20 | Accept | 0.10583 | 1.4718 | 0.10062 | 0.10089 | 9.8999e-07 | svm |
|=====================================================================================================|
| Iter | Eval | Objective: | Objective | BestSoFar | BestSoFar | Lambda | Learner |
| | result | log(1+loss) | runtime | (observed) | (estim.) | | |
|=====================================================================================================|
| 21 | Best | 0.10052 | 0.3996 | 0.10052 | 0.10025 | 0.002124 | leastsquares |
| 22 | Accept | 0.10091 | 0.37174 | 0.10052 | 0.10024 | 8.7079e-08 | leastsquares |
| 23 | Best | 0.10052 | 0.47266 | 0.10052 | 0.10033 | 0.0021352 | leastsquares |
| 24 | Accept | 0.10091 | 0.37863 | 0.10052 | 0.10033 | 8.0672e-09 | leastsquares |
| 25 | Accept | 0.10052 | 0.37939 | 0.10052 | 0.10038 | 0.0021099 | leastsquares |
| 26 | Accept | 0.10091 | 0.42475 | 0.10052 | 0.10038 | 8.5163e-07 | leastsquares |
| 27 | Accept | 0.1009 | 0.38615 | 0.10052 | 0.10038 | 3.8212e-05 | leastsquares |
| 28 | Accept | 0.31858 | 1.2477 | 0.10052 | 0.10046 | 0.17205 | svm |
| 29 | Accept | 0.10574 | 1.3903 | 0.10052 | 0.10047 | 0.00070859 | svm |
| 30 | Accept | 0.10082 | 0.4233 | 0.10052 | 0.10047 | 0.00028825 | leastsquares |
__________________________________________________________
Optimization completed.
MaxObjectiveEvaluations of 30 reached.
Total function evaluations: 30
Total elapsed time: 35.031 seconds
Total objective function evaluation time: 19.7546
Best observed feasible point:
Lambda Learner
_________ ____________
0.0021352 leastsquares
Observed objective function value = 0.10052
Estimated objective function value = 0.10047
Function evaluation time = 0.47266
Best estimated feasible point (according to models):
Lambda Learner
_________ ____________
0.0021352 leastsquares
Estimated objective function value = 0.10047
Estimated function evaluation time = 0.38164
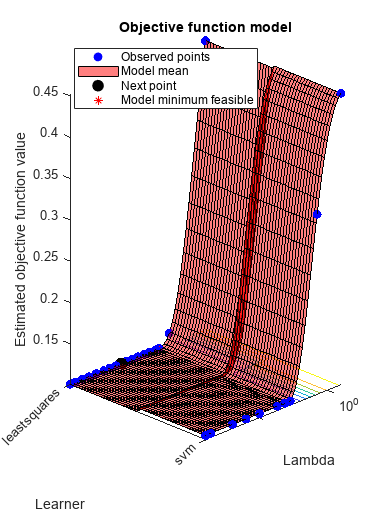
Mdl =
RegressionLinear
ResponseName: 'Y'
ResponseTransform: 'none'
Beta: [1000×1 double]
Bias: -0.0071
Lambda: 0.0021
Learner: 'leastsquares'
Properties, Methods
FitInfo = struct with fields:
Lambda: 0.0021
Objective: 0.0472
IterationLimit: 1000
NumIterations: 15
GradientNorm: 2.4347e-06
GradientTolerance: 1.0000e-06
RelativeChangeInBeta: 3.3860e-05
BetaTolerance: 1.0000e-04
DeltaGradient: []
DeltaGradientTolerance: []
TerminationCode: 1
TerminationStatus: {'Tolerance on coefficients satisfied.'}
History: []
FitTime: 0.0916
Solver: {'lbfgs'}
HyperparameterOptimizationResults =
BayesianOptimization with properties:
ObjectiveFcn: @createObjFcn/inMemoryObjFcn
VariableDescriptions: [3×1 optimizableVariable]
Options: [1×1 struct]
MinObjective: 0.1005
XAtMinObjective: [1×2 table]
MinEstimatedObjective: 0.1005
XAtMinEstimatedObjective: [1×2 table]
NumObjectiveEvaluations: 30
TotalElapsedTime: 35.0310
NextPoint: [1×2 table]
XTrace: [30×2 table]
ObjectiveTrace: [30×1 double]
ConstraintsTrace: []
UserDataTrace: {30×1 cell}
ObjectiveEvaluationTimeTrace: [30×1 double]
IterationTimeTrace: [30×1 double]
ErrorTrace: [30×1 double]
FeasibilityTrace: [30×1 logical]
FeasibilityProbabilityTrace: [30×1 double]
IndexOfMinimumTrace: [30×1 double]
ObjectiveMinimumTrace: [30×1 double]
EstimatedObjectiveMinimumTrace: [30×1 double]
This optimization technique is simpler than that shown in Find Good Lasso Penalty Using Cross-Validation, but does not allow you to trade off model complexity and cross-validation loss.
Input Arguments
Predictor data, specified as an n-by-p full or sparse matrix.
The length of Y and the number of observations
in X must be equal.
Note
If you orient your predictor matrix so that observations correspond to columns and
specify 'ObservationsIn','columns', then you might experience a
significant reduction in optimization execution time.
Data Types: single | double
Sample data used to train the model, specified as a table. Each row of Tbl
corresponds to one observation, and each column corresponds to one predictor variable.
Optionally, Tbl can contain one additional column for the response
variable. Multicolumn variables and cell arrays other than cell arrays of character
vectors are not allowed.
If
Tblcontains the response variable, and you want to use all remaining variables inTblas predictors, then specify the response variable by usingResponseVarName.If
Tblcontains the response variable, and you want to use only a subset of the remaining variables inTblas predictors, then specify a formula by usingformula.If
Tbldoes not contain the response variable, then specify a response variable by usingY. The length of the response variable and the number of rows inTblmust be equal.
Response variable name, specified as the name of a variable in
Tbl. The response variable must be a numeric vector.
You must specify ResponseVarName as a character vector or string
scalar. For example, if Tbl stores the response variable
Y as Tbl.Y, then specify it as
"Y". Otherwise, the software treats all columns of
Tbl, including Y, as predictors when
training the model.
Data Types: char | string
Explanatory model of the response variable and a subset of the predictor variables,
specified as a character vector or string scalar in the form
"Y~x1+x2+x3". In this form, Y represents the
response variable, and x1, x2, and
x3 represent the predictor variables.
To specify a subset of variables in Tbl as predictors for
training the model, use a formula. If you specify a formula, then the software does not
use any variables in Tbl that do not appear in
formula.
The variable names in the formula must be both variable names in Tbl
(Tbl.Properties.VariableNames) and valid MATLAB® identifiers. You can verify the variable names in Tbl by
using the isvarname function. If the variable names
are not valid, then you can convert them by using the matlab.lang.makeValidName function.
Data Types: char | string
Note
The software treats NaN, empty character vector (''), empty string (""), <missing>, and <undefined> elements as missing values, and removes observations with any of these characteristics:
Missing value in the response (for example,
YorValidationData{2})At least one missing value in a predictor observation (for example, row in
XorValidationData{1})NaNvalue or0weight (for example, value inWeightsorValidationData{3})
For memory-usage economy, it is best practice to remove observations containing missing values from your training data manually before training.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: Mdl = fitrlinear(X,Y,'Learner','leastsquares','CrossVal','on','Regularization','lasso') specifies to implement least-squares regression, implement 10-fold cross-validation, and specifies to include a lasso regularization term.
Note
You cannot use any cross-validation name-value argument together with the
OptimizeHyperparameters name-value argument. You can modify the
cross-validation for OptimizeHyperparameters only by using the
HyperparameterOptimizationOptions name-value argument.
Linear Regression Options
Half the width of the epsilon-insensitive band, specified as the comma-separated pair consisting of 'Epsilon' and a nonnegative scalar value. 'Epsilon' applies to SVM learners only.
The default Epsilon value is iqr(Y)/13.49, which is an estimate of standard deviation using the interquartile range of the response variable Y. If iqr(Y) is equal to zero, then the default Epsilon value is 0.1.
Example: 'Epsilon',0.3
Data Types: single | double
Regularization term strength, specified as the comma-separated pair consisting of 'Lambda' and 'auto', a nonnegative scalar, or a vector of nonnegative values.
For
'auto',Lambda= 1/n.If you specify a cross-validation, name-value pair argument (e.g.,
CrossVal), then n is the number of in-fold observations.Otherwise, n is the training sample size.
For a vector of nonnegative values,
fitrlinearsequentially optimizes the objective function for each distinct value inLambdain ascending order.If
Solveris'sgd'or'asgd'andRegularizationis'lasso',fitrlineardoes not use the previous coefficient estimates as a warm start for the next optimization iteration. Otherwise,fitrlinearuses warm starts.If
Regularizationis'lasso', then any coefficient estimate of 0 retains its value whenfitrlinearoptimizes using subsequent values inLambda.fitrlinearreturns coefficient estimates for each specified regularization strength.
Example: 'Lambda',10.^(-(10:-2:2))
Data Types: char | string | double | single
Linear regression model type, specified as the comma-separated pair consisting of 'Learner' and 'svm' or 'leastsquares'.
In this table,
β is a vector of p coefficients.
x is an observation from p predictor variables.
b is the scalar bias.
| Value | Algorithm | Response range | Loss function |
|---|---|---|---|
'leastsquares' | Linear regression via ordinary least squares | y ∊ (-∞,∞) | Mean squared error (MSE): |
'svm' | Support vector machine regression | Same as 'leastsquares' | Epsilon-insensitive: |
Example: 'Learner','leastsquares'
Predictor data observation dimension, specified as "rows" or
"columns".
Note
If you orient your predictor matrix so that observations correspond to columns and
specify ObservationsIn="columns", then you might experience a
significant reduction in computation time. You cannot specify
ObservationsIn="columns" for predictor data in a
table.
Example: ObservationsIn="columns"
Data Types: char | string
Complexity penalty type, specified as the comma-separated pair
consisting of 'Regularization' and 'lasso' or 'ridge'.
The software composes the objective function for minimization
from the sum of the average loss function (see Learner)
and the regularization term in this table.
| Value | Description |
|---|---|
'lasso' | Lasso (L1) penalty: |
'ridge' | Ridge (L2) penalty: |
To specify the regularization term strength, which is λ in
the expressions, use Lambda.
The software excludes the bias term (β0) from the regularization penalty.
If Solver is 'sparsa',
then the default value of Regularization is 'lasso'.
Otherwise, the default is 'ridge'.
Tip
For predictor variable selection, specify
'lasso'. For more on variable selection, see Introduction to Feature Selection.For optimization accuracy, specify
'ridge'.
Example: 'Regularization','lasso'
Objective function minimization technique, specified as the comma-separated pair consisting of 'Solver' and a character vector or string scalar, a string array, or a cell array of character vectors with values from this table.
| Value | Description | Restrictions |
|---|---|---|
'sgd' | Stochastic gradient descent (SGD) [5][3] | |
'asgd' | Average stochastic gradient descent (ASGD) [8] | |
'dual' | Dual SGD for SVM [2][7] | Regularization must be 'ridge' and Learner must be 'svm'. |
'bfgs' | Broyden-Fletcher-Goldfarb-Shanno quasi-Newton algorithm (BFGS) [4] | Inefficient if X is very high-dimensional.
Regularization must be
'ridge'. |
'lbfgs' | Limited-memory BFGS (LBFGS) [4] | Regularization must be 'ridge'. |
'sparsa' | Sparse Reconstruction by Separable Approximation (SpaRSA) [6] | Regularization must be 'lasso'. |
If you specify:
A ridge penalty (see
Regularization) andsize(X,1) <= 100(100 or fewer predictor variables), then the default solver is'bfgs'.An SVM regression model (see
Learner), a ridge penalty, andsize(X,1) > 100(more than 100 predictor variables), then the default solver is'dual'.A lasso penalty and
Xcontains 100 or fewer predictor variables, then the default solver is'sparsa'.
Otherwise, the default solver is
'sgd'. Note that the default solver can change when
you perform hyperparameter optimization. For more information, see Regularization method determines the solver used during hyperparameter optimization.
If you specify a string array or cell array of solver names, then, for
each value in Lambda, the software uses the
solutions of solver j as a warm start for solver
j + 1.
Example: {'sgd' 'lbfgs'} applies SGD to solve the
objective, and uses the solution as a warm start for
LBFGS.
Tip
SGD and ASGD can solve the objective function more quickly than other solvers, whereas LBFGS and SpaRSA can yield more accurate solutions than other solvers. Solver combinations like
{'sgd' 'lbfgs'}and{'sgd' 'sparsa'}can balance optimization speed and accuracy.When choosing between SGD and ASGD, consider that:
SGD takes less time per iteration, but requires more iterations to converge.
ASGD requires fewer iterations to converge, but takes more time per iteration.
If the predictor data is high dimensional and
Regularizationis'ridge', setSolverto any of these combinations:'sgd''asgd''dual'ifLearneris'svm''lbfgs'{'sgd','lbfgs'}{'asgd','lbfgs'}{'dual','lbfgs'}ifLearneris'svm'
Although you can set other combinations, they often lead to solutions with poor accuracy.
If the predictor data is moderate through low dimensional and
Regularizationis'ridge', setSolverto'bfgs'.If
Regularizationis'lasso', setSolverto any of these combinations:'sgd''asgd''sparsa'{'sgd','sparsa'}{'asgd','sparsa'}
Example: 'Solver',{'sgd','lbfgs'}
Initial linear coefficient estimates (β), specified as the comma-separated
pair consisting of 'Beta' and a p-dimensional
numeric vector or a p-by-L numeric matrix.
p is the number of predictor variables after dummy variables are
created for categorical variables (for more details, see
CategoricalPredictors), and L is the number
of regularization-strength values (for more details, see
Lambda).
If you specify a p-dimensional vector, then the software optimizes the objective function L times using this process.
The software optimizes using
Betaas the initial value and the minimum value ofLambdaas the regularization strength.The software optimizes again using the resulting estimate from the previous optimization as a warm start, and the next smallest value in
Lambdaas the regularization strength.The software implements step 2 until it exhausts all values in
Lambda.
If you specify a p-by-L matrix, then the software optimizes the objective function L times. At iteration
j, the software usesBeta(:,as the initial value and, after it sortsj)Lambdain ascending order, usesLambda(as the regularization strength.j)
If you set 'Solver','dual', then the software
ignores Beta.
Data Types: single | double
Initial intercept estimate (b), specified as the comma-separated pair consisting of 'Bias' and a numeric scalar or an L-dimensional numeric vector. L is the number of regularization-strength values (for more details, see Lambda).
If you specify a scalar, then the software optimizes the objective function L times using this process.
The software optimizes using
Biasas the initial value and the minimum value ofLambdaas the regularization strength.The uses the resulting estimate as a warm start to the next optimization iteration, and uses the next smallest value in
Lambdaas the regularization strength.The software implements step 2 until it exhausts all values in
Lambda.
If you specify an L-dimensional vector, then the software optimizes the objective function L times. At iteration
j, the software usesBias(as the initial value and, after it sortsj)Lambdain ascending order, usesLambda(as the regularization strength.j)By default:
Data Types: single | double
Linear model intercept inclusion flag, specified as the comma-separated
pair consisting of 'FitBias' and true or false.
| Value | Description |
|---|---|
true | The software includes the bias term b in the linear model, and then estimates it. |
false | The software sets b = 0 during estimation. |
Example: 'FitBias',false
Data Types: logical
Flag to fit the linear model intercept after optimization, specified as the comma-separated pair consisting of 'PostFitBias' and true or false.
| Value | Description |
|---|---|
false | The software estimates the bias term b and the coefficients β during optimization. |
true | To estimate b, the software:
|
If you specify true, then FitBias must be true.
Example: 'PostFitBias',true
Data Types: logical
Verbosity level, specified as the comma-separated pair consisting
of 'Verbose' and a nonnegative integer. Verbose controls
the amount of diagnostic information fitrlinear displays
at the command line.
| Value | Description |
|---|---|
0 | fitrlinear does not display diagnostic
information. |
1 | fitrlinear periodically displays and
stores the value of the objective function, gradient magnitude, and
other diagnostic information. FitInfo.History contains
the diagnostic information. |
| Any other positive integer | fitrlinear displays and stores diagnostic
information at each optimization iteration. FitInfo.History contains
the diagnostic information. |
Example: 'Verbose',1
Data Types: double | single
SGD and ASGD Solver Options
Mini-batch size, specified as the comma-separated pair consisting
of 'BatchSize' and a positive integer. At each
iteration, the software estimates the subgradient using BatchSize observations
from the training data.
If
Xis a numeric matrix, then the default value is10.If
Xis a sparse matrix, then the default value ismax([10,ceil(sqrt(ff))]), whereff = numel(X)/nnz(X)(the fullness factor ofX).
Example: 'BatchSize',100
Data Types: single | double
Learning rate, specified as the comma-separated pair consisting of 'LearnRate' and a positive scalar. LearnRate specifies how many steps to take per iteration. At each iteration, the gradient specifies the direction and magnitude of each step.
If
Regularizationis'ridge', thenLearnRatespecifies the initial learning rate γ0. The software determines the learning rate for iteration t, γt, usingIf
Regularizationis'lasso', then, for all iterations,LearnRateis constant.
By default, LearnRate is 1/sqrt(1+max((sum(X.^2,obsDim)))), where obsDim is 1 if the observations compose the columns of X, and 2 otherwise.
Example: 'LearnRate',0.01
Data Types: single | double
Flag to decrease the learning rate when the software detects
divergence (that is, over-stepping the minimum), specified as the
comma-separated pair consisting of 'OptimizeLearnRate' and true or false.
If OptimizeLearnRate is 'true',
then:
For the few optimization iterations, the software starts optimization using
LearnRateas the learning rate.If the value of the objective function increases, then the software restarts and uses half of the current value of the learning rate.
The software iterates step 2 until the objective function decreases.
Example: 'OptimizeLearnRate',true
Data Types: logical
Number of mini-batches between lasso truncation runs, specified
as the comma-separated pair consisting of 'TruncationPeriod' and
a positive integer.
After a truncation run, the software applies a soft threshold
to the linear coefficients. That is, after processing k = TruncationPeriod mini-batches,
the software truncates the estimated coefficient j using
For SGD, is the estimate of coefficient j after processing k mini-batches. γt is the learning rate at iteration t. λ is the value of
Lambda.For ASGD, is the averaged estimate coefficient j after processing k mini-batches,
If Regularization is 'ridge',
then the software ignores TruncationPeriod.
Example: 'TruncationPeriod',100
Data Types: single | double
Other Regression Options
Categorical predictors list, specified as one of the values in this table. The descriptions assume that the predictor data has observations in rows and predictors in columns.
| Value | Description |
|---|---|
| Vector of positive integers |
Each entry in the vector is an index value indicating that the corresponding predictor is
categorical. The index values are between 1 and If |
| Logical vector |
A |
| Character matrix | Each row of the matrix is the name of a predictor variable. The names must match the entries in PredictorNames. Pad the names with extra blanks so each row of the character matrix has the same length. |
| String array or cell array of character vectors | Each element in the array is the name of a predictor variable. The names must match the entries in PredictorNames. |
"all" | All predictors are categorical. |
By default, if the
predictor data is in a table (Tbl), fitrlinear
assumes that a variable is categorical if it is a logical vector, categorical vector, character
array, string array, or cell array of character vectors. If the predictor data is a matrix
(X), fitrlinear assumes that all predictors are
continuous. To identify any other predictors as categorical predictors, specify them by using
the CategoricalPredictors name-value argument.
For the identified categorical predictors, fitrlinear creates
dummy variables using two different schemes, depending on whether a categorical variable
is unordered or ordered. For an unordered categorical variable,
fitrlinear creates one dummy variable for each level of the
categorical variable. For an ordered categorical variable,
fitrlinear creates one less dummy variable than the number of
categories. For details, see Automatic Creation of Dummy Variables.
Example: CategoricalPredictors="all"
Data Types: single | double | logical | char | string | cell
Predictor variable names, specified as a string array of unique names or cell array of unique
character vectors. The functionality of PredictorNames depends on the
way you supply the training data.
If you supply
XandY, then you can usePredictorNamesto assign names to the predictor variables inX.The order of the names in
PredictorNamesmust correspond to the predictor order inX. Assuming thatXhas the default orientation, with observations in rows and predictors in columns,PredictorNames{1}is the name ofX(:,1),PredictorNames{2}is the name ofX(:,2), and so on. Also,size(X,2)andnumel(PredictorNames)must be equal.By default,
PredictorNamesis{'x1','x2',...}.
If you supply
Tbl, then you can usePredictorNamesto choose which predictor variables to use in training. That is,fitrlinearuses only the predictor variables inPredictorNamesand the response variable during training.PredictorNamesmust be a subset ofTbl.Properties.VariableNamesand cannot include the name of the response variable.By default,
PredictorNamescontains the names of all predictor variables.A good practice is to specify the predictors for training using either
PredictorNamesorformula, but not both.
Example: PredictorNames=["SepalLength","SepalWidth","PetalLength","PetalWidth"]
Data Types: string | cell
Response variable name, specified as a character vector or string scalar.
If you supply
Y, then you can useResponseNameto specify a name for the response variable.If you supply
ResponseVarNameorformula, then you cannot useResponseName.
Example: ResponseName="response"
Data Types: char | string
Function for transforming raw response values, specified as a function handle or
function name. The default is "none", which means
@(y)y, or no transformation. The function should accept a vector
(the original response values) and return a vector of the same size (the transformed
response values).
Example: Suppose you create a function handle that applies an exponential
transformation to an input vector by using myfunction = @(y)exp(y).
Then, you can specify the response transformation as
ResponseTransform=myfunction.
Data Types: char | string | function_handle
Observation weights, specified as the comma-separated pair consisting of 'Weights' and a positive numeric vector or the name of a variable in Tbl. The software weights each observation in X or Tbl with the corresponding value in Weights. The length of Weights must equal the number of observations in X or Tbl.
If you specify the input data as a table Tbl, then Weights can be the name of a variable in Tbl that contains a numeric vector. In this case, you must specify Weights as a character vector or string scalar. For example, if weights vector W is stored as Tbl.W, then specify it as 'W'. Otherwise, the software treats all columns of Tbl, including W, as predictors when training the model.
By default, Weights is ones(n,1), where n is the number of observations in X or Tbl.
fitrlinear normalizes the weights to sum to 1.
Inf weights are not supported.
Data Types: single | double | char | string
Cross-Validation Options
Cross-validation flag, specified as the comma-separated pair
consisting of 'Crossval' and 'on' or 'off'.
If you specify 'on', then the software implements
10-fold cross-validation.
To override this cross-validation setting, use one of these name-value pair arguments:
CVPartition, Holdout,
KFold, or Leaveout. To create a
cross-validated model, you can use one cross-validation name-value pair argument at a
time only.
Example: 'Crossval','on'
Cross-validation partition, specified as the comma-separated
pair consisting of 'CVPartition' and a cvpartition partition
object as created by cvpartition.
The partition object specifies the type of cross-validation, and also
the indexing for training and validation sets.
To create a cross-validated model, you can use one of these four options only:
CVPartition, Holdout,
KFold, or Leaveout.
Fraction of data used for holdout validation, specified as the
comma-separated pair consisting of 'Holdout' and
a scalar value in the range (0,1). If you specify 'Holdout',,
then the software: p
Randomly reserves
p*100Stores the compact, trained model in the
Trainedproperty of the cross-validated model.
To create a cross-validated model, you can use one of these four options only:
CVPartition, Holdout,
KFold, or Leaveout.
Example: 'Holdout',0.1
Data Types: double | single
Number of folds to use in a cross-validated classifier, specified
as the comma-separated pair consisting of 'KFold' and
a positive integer value greater than 1. If you specify, e.g., 'KFold',k,
then the software:
Randomly partitions the data into k sets
For each set, reserves the set as validation data, and trains the model using the other k – 1 sets
Stores the
kcompact, trained models in the cells of ak-by-1 cell vector in theTrainedproperty of the cross-validated model.
To create a cross-validated model, you can use one of these four options only:
CVPartition,
Holdout,
KFold, or
Leaveout.
Example: 'KFold',8
Data Types: single | double
Leave-one-out cross-validation, specified as "off" or "on".
If you specify Leaveout as "on", then for each
observation, fitrlinear reserves the observation as test data, and
trains the model using the other observations.
You can use only one of these name-value arguments: CVPartition,
Holdout, KFold, or
Leaveout.
Example: Leaveout="on"
Data Types: single | double
SGD and ASGD Convergence Controls
Maximal number of batches to process, specified as the comma-separated
pair consisting of 'BatchLimit' and a positive
integer. When the software processes BatchLimit batches,
it terminates optimization.
By default:
If you specify
BatchLimit, thenfitrlinearuses the argument that results in processing the fewest observations, eitherBatchLimitorPassLimit.
Example: 'BatchLimit',100
Data Types: single | double
Relative tolerance on the linear coefficients and the bias term (intercept), specified
as the comma-separated pair consisting of 'BetaTolerance' and a
nonnegative scalar.
Let , that is, the vector of the coefficients and the bias term at optimization iteration t. If , then optimization terminates.
If the software converges for the last solver specified in
Solver, then optimization terminates. Otherwise, the software uses
the next solver specified in Solver.
Example: 'BetaTolerance',1e-6
Data Types: single | double
Number of batches to process before next convergence check, specified as the
comma-separated pair consisting of 'NumCheckConvergence' and a
positive integer.
To specify the batch size, see BatchSize.
The software checks for convergence about 10 times per pass through the entire data set by default.
Example: 'NumCheckConvergence',100
Data Types: single | double
Maximal number of passes through the data, specified as the comma-separated pair consisting of 'PassLimit' and a positive integer.
fitrlinear processes all observations when it completes one pass through the data.
When fitrlinear passes through the data PassLimit times, it terminates optimization.
If you specify BatchLimit, then
fitrlinear uses the argument that results in
processing the fewest observations, either
BatchLimit or PassLimit.
For more details, see Algorithms.
Example: 'PassLimit',5
Data Types: single | double
Validation data for optimization convergence detection, specified as the comma-separated pair
consisting of 'ValidationData' and a cell array or table.
During optimization, the software periodically estimates the loss of ValidationData. If the validation-data loss increases, then the software terminates optimization. For more details, see Algorithms. To optimize hyperparameters using cross-validation, see cross-validation options such as CrossVal.
You can specify ValidationData as a table if you use a table
Tbl of predictor data that contains the response variable. In this
case, ValidationData must contain the same predictors and response
contained in Tbl. The software does not apply weights to observations,
even if Tbl contains a vector of weights. To specify weights, you must
specify ValidationData as a cell array.
If you specify ValidationData as a cell array, then it must have the
following format:
ValidationData{1}must have the same data type and orientation as the predictor data. That is, if you use a predictor matrixX, thenValidationData{1}must be an m-by-p or p-by-m full or sparse matrix of predictor data that has the same orientation asX. The predictor variables in the training dataXandValidationData{1}must correspond. Similarly, if you use a predictor tableTblof predictor data, thenValidationData{1}must be a table containing the same predictor variables contained inTbl. The number of observations inValidationData{1}and the predictor data can vary.ValidationData{2}must match the data type and format of the response variable, eitherYorResponseVarName. IfValidationData{2}is an array of responses, then it must have the same number of elements as the number of observations inValidationData{1}. IfValidationData{1}is a table, thenValidationData{2}can be the name of the response variable in the table. If you want to use the sameResponseVarNameorformula, you can specifyValidationData{2}as[].Optionally, you can specify
ValidationData{3}as an m-dimensional numeric vector of observation weights or the name of a variable in the tableValidationData{1}that contains observation weights. The software normalizes the weights with the validation data so that they sum to 1.
If you specify ValidationData and want to display the validation loss at
the command line, specify a value larger than 0 for Verbose.
If the software converges for the last solver specified in Solver, then optimization terminates. Otherwise, the software uses the next solver specified in Solver.
By default, the software does not detect convergence by monitoring validation-data loss.
Absolute gradient tolerance, specified as the comma-separated pair consisting of 'GradientTolerance' and a nonnegative scalar. GradientTolerance applies to these values of Solver: 'bfgs', 'lbfgs', and 'sparsa'.
Let be the gradient vector of the objective function with respect to the coefficients and bias term at optimization iteration t. If , then optimization terminates.
If you also specify BetaTolerance, then optimization terminates when fitrlinear satisfies either stopping criterion.
If fitrlinear converges for the last solver specified in Solver, then optimization terminates. Otherwise, fitrlinear uses the next solver specified in Solver.
Example: 'GradientTolerance',eps
Data Types: single | double
Maximal number of optimization iterations, specified as the comma-separated pair consisting of 'IterationLimit' and a positive integer. IterationLimit applies to these values of Solver: 'bfgs', 'lbfgs', and 'sparsa'.
Example: 'IterationLimit',1e7
Data Types: single | double
Dual SGD Optimization Convergence Controls
Relative tolerance on the linear coefficients and the bias term (intercept), specified
as the comma-separated pair consisting of 'BetaTolerance' and a
nonnegative scalar.
Let , that is, the vector of the coefficients and the bias term at optimization iteration t. If , then optimization terminates.
If you also specify DeltaGradientTolerance, then optimization
terminates when the software satisfies either stopping criterion.
If the software converges for the last solver specified in
Solver, then optimization terminates. Otherwise, the software uses
the next solver specified in Solver.
Example: 'BetaTolerance',1e-6
Data Types: single | double
Gradient-difference tolerance between upper and lower pool Karush-Kuhn-Tucker
(KKT) complementarity conditions violators, specified as a
nonnegative scalar. DeltaGradientTolerance applies to
the 'dual' value of Solver
only.
If the magnitude of the KKT violators is less than
DeltaGradientTolerance, thenfitrlinearterminates optimization.If
fitrlinearconverges for the last solver specified inSolver, then optimization terminates. Otherwise,fitrlinearuses the next solver specified inSolver.
Example: 'DeltaGradientTolerance',1e-2
Data Types: double | single
Number of passes through entire data set to process before next convergence check,
specified as the comma-separated pair consisting of
'NumCheckConvergence' and a positive integer.
Example: 'NumCheckConvergence',100
Data Types: single | double
Maximal number of passes through the data, specified as the
comma-separated pair consisting of 'PassLimit' and
a positive integer.
When the software completes one pass through the data, it has processed all observations.
When the software passes through the data PassLimit times,
it terminates optimization.
Example: 'PassLimit',5
Data Types: single | double
Validation data for optimization convergence detection, specified as the comma-separated pair
consisting of 'ValidationData' and a cell array or table.
During optimization, the software periodically estimates the loss of ValidationData. If the validation-data loss increases, then the software terminates optimization. For more details, see Algorithms. To optimize hyperparameters using cross-validation, see cross-validation options such as CrossVal.
You can specify ValidationData as a table if you use a table
Tbl of predictor data that contains the response variable. In this
case, ValidationData must contain the same predictors and response
contained in Tbl. The software does not apply weights to observations,
even if Tbl contains a vector of weights. To specify weights, you must
specify ValidationData as a cell array.
If you specify ValidationData as a cell array, then it must have the
following format:
ValidationData{1}must have the same data type and orientation as the predictor data. That is, if you use a predictor matrixX, thenValidationData{1}must be an m-by-p or p-by-m full or sparse matrix of predictor data that has the same orientation asX. The predictor variables in the training dataXandValidationData{1}must correspond. Similarly, if you use a predictor tableTblof predictor data, thenValidationData{1}must be a table containing the same predictor variables contained inTbl. The number of observations inValidationData{1}and the predictor data can vary.ValidationData{2}must match the data type and format of the response variable, eitherYorResponseVarName. IfValidationData{2}is an array of responses, then it must have the same number of elements as the number of observations inValidationData{1}. IfValidationData{1}is a table, thenValidationData{2}can be the name of the response variable in the table. If you want to use the sameResponseVarNameorformula, you can specifyValidationData{2}as[].Optionally, you can specify
ValidationData{3}as an m-dimensional numeric vector of observation weights or the name of a variable in the tableValidationData{1}that contains observation weights. The software normalizes the weights with the validation data so that they sum to 1.
If you specify ValidationData and want to display the validation loss at
the command line, specify a value larger than 0 for Verbose.
If the software converges for the last solver specified in Solver, then optimization terminates. Otherwise, the software uses the next solver specified in Solver.
By default, the software does not detect convergence by monitoring validation-data loss.
BFGS, LBFGS, and SpaRSA Convergence Controls
Relative tolerance on the linear coefficients and the bias term (intercept), specified as a nonnegative scalar.
Let , that is, the vector of the coefficients and the bias term at optimization iteration t. If , then optimization terminates.
If you also specify GradientTolerance, then optimization terminates when the software satisfies either stopping criterion.
If the software converges for the last solver specified in
Solver, then optimization terminates. Otherwise, the software uses
the next solver specified in Solver.
Example: 'BetaTolerance',1e-6
Data Types: single | double
Absolute gradient tolerance, specified as a nonnegative scalar.
Let be the gradient vector of the objective function with respect to the coefficients and bias term at optimization iteration t. If , then optimization terminates.
If you also specify BetaTolerance, then optimization terminates when the
software satisfies either stopping criterion.
If the software converges for the last solver specified in the
software, then optimization terminates. Otherwise, the software uses
the next solver specified in Solver.
Example: 'GradientTolerance',1e-5
Data Types: single | double
Size of history buffer for Hessian approximation, specified
as the comma-separated pair consisting of 'HessianHistorySize' and
a positive integer. That is, at each iteration, the software composes
the Hessian using statistics from the latest HessianHistorySize iterations.
The software does not support 'HessianHistorySize' for
SpaRSA.
Example: 'HessianHistorySize',10
Data Types: single | double
Maximal number of optimization iterations, specified as the
comma-separated pair consisting of 'IterationLimit' and
a positive integer. IterationLimit applies to these
values of Solver: 'bfgs', 'lbfgs',
and 'sparsa'.
Example: 'IterationLimit',500
Data Types: single | double
Validation data for optimization convergence detection, specified as the comma-separated pair
consisting of 'ValidationData' and a cell array or table.
During optimization, the software periodically estimates the loss of ValidationData. If the validation-data loss increases, then the software terminates optimization. For more details, see Algorithms. To optimize hyperparameters using cross-validation, see cross-validation options such as CrossVal.
You can specify ValidationData as a table if you use a table
Tbl of predictor data that contains the response variable. In this
case, ValidationData must contain the same predictors and response
contained in Tbl. The software does not apply weights to observations,
even if Tbl contains a vector of weights. To specify weights, you must
specify ValidationData as a cell array.
If you specify ValidationData as a cell array, then it must have the
following format:
ValidationData{1}must have the same data type and orientation as the predictor data. That is, if you use a predictor matrixX, thenValidationData{1}must be an m-by-p or p-by-m full or sparse matrix of predictor data that has the same orientation asX. The predictor variables in the training dataXandValidationData{1}must correspond. Similarly, if you use a predictor tableTblof predictor data, thenValidationData{1}must be a table containing the same predictor variables contained inTbl. The number of observations inValidationData{1}and the predictor data can vary.ValidationData{2}must match the data type and format of the response variable, eitherYorResponseVarName. IfValidationData{2}is an array of responses, then it must have the same number of elements as the number of observations inValidationData{1}. IfValidationData{1}is a table, thenValidationData{2}can be the name of the response variable in the table. If you want to use the sameResponseVarNameorformula, you can specifyValidationData{2}as[].Optionally, you can specify
ValidationData{3}as an m-dimensional numeric vector of observation weights or the name of a variable in the tableValidationData{1}that contains observation weights. The software normalizes the weights with the validation data so that they sum to 1.
If you specify ValidationData and want to display the validation loss at
the command line, specify a value larger than 0 for Verbose.
If the software converges for the last solver specified in Solver, then optimization terminates. Otherwise, the software uses the next solver specified in Solver.
By default, the software does not detect convergence by monitoring validation-data loss.
Hyperparameter Optimization
Parameters to optimize, specified as the comma-separated pair consisting of 'OptimizeHyperparameters' and one of the following:
'none'— Do not optimize.'auto'— Use{'Lambda','Learner'}.'all'— Optimize all eligible parameters.String array or cell array of eligible parameter names.
Vector of
optimizableVariableobjects, typically the output ofhyperparameters.
The optimization attempts to minimize the cross-validation loss
(error) for fitrlinear by varying the parameters. To control the
cross-validation type and other aspects of the optimization, use the
HyperparameterOptimizationOptions name-value argument. When you use
HyperparameterOptimizationOptions, you can use the (compact) model size
instead of the cross-validation loss as the optimization objective by setting the
ConstraintType and ConstraintBounds options.
Note
The values of OptimizeHyperparameters override any values you
specify using other name-value arguments. For example, setting
OptimizeHyperparameters to "auto" causes
fitrlinear to optimize hyperparameters corresponding to the
"auto" option and to ignore any specified values for the
hyperparameters.
The eligible parameters for fitrlinear are:
Lambda—fitrlinearsearches among positive values, by default log-scaled in the range[1e-5/NumObservations,1e5/NumObservations].Learner—fitrlinearsearches among'svm'and'leastsquares'.Regularization—fitrlinearsearches among'ridge'and'lasso'.When
Regularizationis'ridge', the function sets theSolvervalue to'lbfgs'by default.When
Regularizationis'lasso', the function sets theSolvervalue to'sparsa'by default.
Set nondefault parameters by passing a vector of optimizableVariable objects that have nondefault values. For example,
load carsmall params = hyperparameters('fitrlinear',[Horsepower,Weight],MPG); params(1).Range = [1e-3,2e4];
Pass params as the value of OptimizeHyperparameters.
By default, the iterative display appears at the command line,
and plots appear according to the number of hyperparameters in the optimization. For the
optimization and plots, the objective function is log(1 + cross-validation loss). To control the iterative display, set the Verbose option
of the HyperparameterOptimizationOptions name-value argument. To control
the plots, set the ShowPlots option of the
HyperparameterOptimizationOptions name-value argument.
For an example, see Optimize a Linear Regression.
Example: 'OptimizeHyperparameters','auto'
Options for optimization, specified as a HyperparameterOptimizationOptions object or a structure. This argument
modifies the effect of the OptimizeHyperparameters name-value
argument. If you specify HyperparameterOptimizationOptions, you must
also specify OptimizeHyperparameters. All the options are optional.
However, you must set ConstraintBounds and
ConstraintType to return
AggregateOptimizationResults. The options that you can set in a
structure are the same as those in the
HyperparameterOptimizationOptions object.
| Option | Values | Default |
|---|---|---|
Optimizer |
| "bayesopt" |
ConstraintBounds | Constraint bounds for N optimization problems,
specified as an N-by-2 numeric matrix or
| [] |
ConstraintTarget | Constraint target for the optimization problems, specified as
| If you specify ConstraintBounds and
ConstraintType, then the default value is
"matlab". Otherwise, the default value is
[]. |
ConstraintType | Constraint type for the optimization problems, specified as
| [] |
AcquisitionFunctionName | Type of acquisition function:
Acquisition functions whose names include
| "expected-improvement-per-second-plus" |
MaxObjectiveEvaluations | Maximum number of objective function evaluations. If you specify multiple
optimization problems using ConstraintBounds, the value of
MaxObjectiveEvaluations applies to each optimization
problem individually. | 30 for "bayesopt" and
"randomsearch", and the entire grid for
"gridsearch" |
MaxTime | Time limit for the optimization, specified as a nonnegative real
scalar. The time limit is in seconds, as measured by | Inf |
NumGridDivisions | For Optimizer="gridsearch", the number of values in each
dimension. The value can be a vector of positive integers giving the number of
values for each dimension, or a scalar that applies to all dimensions. The
software ignores this option for categorical variables. | 10 |
ShowPlots | Logical value indicating whether to show plots of the optimization progress.
If this option is true, the software plots the best observed
objective function value against the iteration number. If you use Bayesian
optimization (Optimizer="bayesopt"), the
software also plots the best estimated objective function value. The best
observed objective function values and best estimated objective function values
correspond to the values in the BestSoFar (observed) and
BestSoFar (estim.) columns of the iterative display,
respectively. You can find these values in the properties ObjectiveMinimumTrace and EstimatedObjectiveMinimumTrace of
Mdl.HyperparameterOptimizationResults. If the problem
includes one or two optimization parameters for Bayesian optimization, then
ShowPlots also plots a model of the objective function
against the parameters. | true |
SaveIntermediateResults | Logical value indicating whether to save the optimization results. If this
option is true, the software overwrites a workspace variable
named "BayesoptResults" at each iteration. The variable is a
BayesianOptimization object. If you
specify multiple optimization problems using
ConstraintBounds, the workspace variable is an AggregateBayesianOptimization object named
"AggregateBayesoptResults". | false |
Verbose | Display level at the command line:
For details, see the | 1 |
UseParallel | Logical value indicating whether to run the Bayesian optimization in parallel, which requires Parallel Computing Toolbox™. Due to the nonreproducibility of parallel timing, parallel Bayesian optimization does not necessarily yield reproducible results. For details, see Parallel Bayesian Optimization. | false |
Repartition | Logical value indicating whether to repartition the cross-validation at
every iteration. If this option is A value of
| false |
| Specify only one of the following three options. | ||
CVPartition | cvpartition object created by cvpartition | KFold=5 if you do not specify a
cross-validation option |
Holdout | Scalar in the range (0,1) representing the holdout
fraction | |
KFold | Integer greater than 1 | |
Example: HyperparameterOptimizationOptions=struct(UseParallel=true)
Output Arguments
Trained linear regression model, returned as a RegressionLinear model object or
RegressionPartitionedLinear
cross-validated model object.
If you set any of the name-value pair arguments
KFold, Holdout,
CrossVal, or CVPartition, then
Mdl is a
RegressionPartitionedLinear cross-validated model
object. Otherwise, Mdl is a
RegressionLinear model object.
To reference properties of Mdl, use dot notation. For
example, enter Mdl.Beta in the Command Window to display
the vector or matrix of estimated coefficients.
If you specify OptimizeHyperparameters and
set the ConstraintType and ConstraintBounds options of
HyperparameterOptimizationOptions, then Mdl is an
N-by-1 cell array of model objects, where N is equal
to the number of rows in ConstraintBounds. If none of the optimization
problems yields a feasible model, then each cell array value is [].
Note
Unlike other regression models, and for economical memory usage,
RegressionLinear and
RegressionPartitionedLinear model objects do not
store the training data or optimization details (for example,
convergence history).
Aggregate optimization results for multiple optimization problems, returned as an AggregateBayesianOptimization object. To return
AggregateOptimizationResults, you must specify
OptimizeHyperparameters and
HyperparameterOptimizationOptions. You must also specify the
ConstraintType and ConstraintBounds
options of HyperparameterOptimizationOptions. For an example that
shows how to produce this output, see Hyperparameter Optimization with Multiple Constraint Bounds.
Optimization details, returned as a structure array.
Fields specify final values or name-value pair argument specifications,
for example, Objective is the value of the objective
function when optimization terminates. Rows of multidimensional fields
correspond to values of Lambda and columns correspond
to values of Solver.
This table describes some notable fields.
| Field | Description | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
TerminationStatus |
| ||||||||||||||
FitTime | Elapsed, wall-clock time in seconds | ||||||||||||||
History | A structure array of optimization information for each
iteration. The field
|
To access fields, use dot notation.
For example, to access the vector of objective function values for
each iteration, enter FitInfo.History.Objective.
If you specify
OptimizeHyperparameters and set the
ConstraintType and ConstraintBounds
options of HyperparameterOptimizationOptions, then
Fitinfo is an N-by-1 cell array of structure
arrays, where N is equal to the number of rows in
ConstraintBounds.
It is good practice to examine FitInfo to
assess whether convergence is satisfactory.
Cross-validation optimization of hyperparameters, returned as a BayesianOptimization object, an AggregateBayesianOptimization object, or a table of hyperparameters and
associated values. The output is nonempty when
OptimizeHyperparameters has a value other than
"none".
If you set the ConstraintType and
ConstraintBounds options in
HyperparameterOptimizationOptions, then
HyperparameterOptimizationResults is an AggregateBayesianOptimization object. Otherwise, the value of
HyperparameterOptimizationResults depends on the value of the
Optimizer option in
HyperparameterOptimizationOptions.
Value of Optimizer Option | Value of HyperparameterOptimizationResults |
|---|---|
"bayesopt" (default) | Object of class BayesianOptimization |
"gridsearch" or "randomsearch" | Table of hyperparameters used, observed objective function values (cross-validation loss), and rank of observations from lowest (best) to highest (worst) |
Note
If Learner is 'leastsquares', then the loss term in the objective function is half of the MSE. loss returns the MSE by default. Therefore, if you use loss to check the resubstitution, or training, error then there is a discrepancy between the MSE returned by loss and optimization results in FitInfo or returned to the command line by setting a positive verbosity level using Verbose.
More About
A warm start is initial estimates of the beta coefficients and bias term supplied to an optimization routine for quicker convergence.
fitclinear and fitrlinear minimize
objective functions relatively quickly for a high-dimensional linear model at the cost of
some accuracy and with the restriction that the model must be linear with respect to the
parameters. If your predictor data set is low- to medium-dimensional, you can use an
alternative classification or regression fitting function. To help you decide which fitting
function is appropriate for your data set, use this table.
| Model to Fit | Function | Notable Algorithmic Differences |
|---|---|---|
| SVM |
| |
| Linear regression |
| |
| Logistic regression |
|
Tips
It is a best practice to orient your predictor matrix so that observations correspond to columns and to specify
'ObservationsIn','columns'. As a result, you can experience a significant reduction in optimization-execution time.If your predictor data has few observations but many predictor variables, then:
Specify
'PostFitBias',true.For SGD or ASGD solvers, set
PassLimitto a positive integer that is greater than 1, for example, 5 or 10. This setting often results in better accuracy.
For SGD and ASGD solvers,
BatchSizeaffects the rate of convergence.If
BatchSizeis too small, thenfitrlinearachieves the minimum in many iterations, but computes the gradient per iteration quickly.If
BatchSizeis too large, thenfitrlinearachieves the minimum in fewer iterations, but computes the gradient per iteration slowly.
Large learning rates (see
LearnRate) speed up convergence to the minimum, but can lead to divergence (that is, over-stepping the minimum). Small learning rates ensure convergence to the minimum, but can lead to slow termination.When using lasso penalties, experiment with various values of
TruncationPeriod. For example, setTruncationPeriodto1,10, and then100.For efficiency,
fitrlineardoes not standardize predictor data. To standardizeXwhere you orient the observations as the columns, enterX = normalize(X,2);
If you orient the observations as the rows, enter
X = normalize(X);
For memory-usage economy, the code replaces the original predictor data the standardized data.
After training a model, you can generate C/C++ code that predicts responses for new data. Generating C/C++ code requires MATLAB Coder™. For details, see Introduction to Code Generation.
Algorithms
If you specify
ValidationData, then, during objective-function optimization:fitrlinearestimates the validation loss ofValidationDataperiodically using the current model, and tracks the minimal estimate.When
fitrlinearestimates a validation loss, it compares the estimate to the minimal estimate.When subsequent, validation loss estimates exceed the minimal estimate five times,
fitrlinearterminates optimization.
If you specify
ValidationDataand to implement a cross-validation routine (CrossVal,CVPartition,Holdout, orKFold), then:fitrlinearrandomly partitionsXandY(orTbl) according to the cross-validation routine that you choose.fitrlineartrains the model using the training-data partition. During objective-function optimization,fitrlinearusesValidationDataas another possible way to terminate optimization (for details, see the previous bullet).Once
fitrlinearsatisfies a stopping criterion, it constructs a trained model based on the optimized linear coefficients and intercept.If you implement k-fold cross-validation, and
fitrlinearhas not exhausted all training-set folds, thenfitrlinearreturns to Step 2 to train using the next training-set fold.Otherwise,
fitrlinearterminates training, and then returns the cross-validated model.
You can determine the quality of the cross-validated model. For example:
To determine the validation loss using the holdout or out-of-fold data from step 1, pass the cross-validated model to
kfoldLoss.To predict observations on the holdout or out-of-fold data from step 1, pass the cross-validated model to
kfoldPredict.
References
[1] Ho, C. H. and C. J. Lin. “Large-Scale Linear Support Vector Regression.” Journal of Machine Learning Research, Vol. 13, 2012, pp. 3323–3348.
[2] Hsieh, C. J., K. W. Chang, C. J. Lin, S. S. Keerthi, and S. Sundararajan. “A Dual Coordinate Descent Method for Large-Scale Linear SVM.” Proceedings of the 25th International Conference on Machine Learning, ICML ’08, 2001, pp. 408–415.
[3] Langford, J., L. Li, and T. Zhang. “Sparse Online Learning Via Truncated Gradient.” J. Mach. Learn. Res., Vol. 10, 2009, pp. 777–801.
[4] Nocedal, J. and S. J. Wright. Numerical Optimization, 2nd ed., New York: Springer, 2006.
[5] Shalev-Shwartz, S., Y. Singer, and N. Srebro. “Pegasos: Primal Estimated Sub-Gradient Solver for SVM.” Proceedings of the 24th International Conference on Machine Learning, ICML ’07, 2007, pp. 807–814.
[6] Wright, S. J., R. D. Nowak, and M. A. T. Figueiredo. “Sparse Reconstruction by Separable Approximation.” Trans. Sig. Proc., Vol. 57, No 7, 2009, pp. 2479–2493.
[7] Xiao, Lin. “Dual Averaging Methods for Regularized Stochastic Learning and Online Optimization.” J. Mach. Learn. Res., Vol. 11, 2010, pp. 2543–2596.
[8] Xu, Wei. “Towards Optimal One Pass Large Scale Learning with Averaged Stochastic Gradient Descent.” CoRR, abs/1107.2490, 2011.
Extended Capabilities
The
fitrlinear function supports tall arrays with the following usage
notes and limitations:
fitrlineardoes not support talltabledata.Some name-value pair arguments have different defaults and values compared to the in-memory
fitrlinearfunction. Supported name-value pair arguments, and any differences, are:'Epsilon''ObservationsIn'— Supports only'rows'.'Lambda'— Can be'auto'(default) or a scalar.'Learner''Regularization'— Supports only'ridge'.'Solver'— Supports only'lbfgs'.'Verbose'— Default value is1'Beta''Bias''FitBias'— Supports onlytrue.'Weights'— Value must be a tall array.'HessianHistorySize''BetaTolerance'— Default value is relaxed to1e-3.'GradientTolerance'— Default value is relaxed to1e-3.'IterationLimit'— Default value is relaxed to20.'OptimizeHyperparameters'— Value of'Regularization'parameter must be'ridge'.'HyperparameterOptimizationOptions'— For cross-validation, tall optimization supports only'Holdout'validation. By default, the software selects and reserves 20% of the data as holdout validation data, and trains the model using the rest of the data. You can specify a different value for the holdout fraction by using this argument. For example, specify'HyperparameterOptimizationOptions',struct('Holdout',0.3)to reserve 30% of the data as validation data.
For tall arrays
fitrlinearimplements LBFGS by distributing the calculation of the loss and the gradient among different parts of the tall array at each iteration. Other solvers are not available for tall arrays.When initial values for
BetaandBiasare not given,fitrlinearfirst refines the initial estimates of the parameters by fitting the model locally to parts of the data and combining the coefficients by averaging.
For more information, see Tall Arrays.
To perform parallel hyperparameter optimization, use the UseParallel=true
option in the HyperparameterOptimizationOptions name-value argument in
the call to the fitrlinear function.
For more information on parallel hyperparameter optimization, see Parallel Bayesian Optimization.
For general information about parallel computing, see Run MATLAB Functions with Automatic Parallel Support (Parallel Computing Toolbox).
The fitrlinear function
supports GPU array input with these usage notes and limitations:
Xcannot be sparse.You cannot specify the
Solvername-value argument as"sgd","asgd", or"dual". ForgpuArrayinputs, the default solver is:"bfgs"when you specify a ridge penalty and fewer than101predictor variables"lbfgs"when you specify a ridge penalty and more than100predictor variables"sparsa"when you specify a lasso penalty
fitrlinearfits the model on a GPU if at least one of the following applies:The input argument
Xis agpuArrayobject.The input argument
Yis agpuArrayobject.The input argument
TblcontainsgpuArraypredictor or response variables.
Version History
Introduced in R2016afitrlinear defaults to serial hyperparameter optimization when
HyperparameterOptimizationOptions includes
UseParallel=true and the software cannot open a parallel pool.
In previous releases, the software issues an error under these circumstances.
fitrlinear now supports GPU arrays with some
limitations.
Starting in R2022a, when you specify to optimize hyperparameters and do not
specify a Solver value, fitrlinear uses
either a Limited-memory BFGS (LBFGS) solver or a Sparse Reconstruction by Separable
Approximation (SpaRSA) solver, depending on the regularization type selected during
each iteration of the hyperparameter optimization.
When
Regularizationis'ridge', the function sets theSolvervalue to'lbfgs'by default.When
Regularizationis'lasso', the function sets theSolvervalue to'sparsa'by default.
In previous releases, the default solver selection during hyperparameter
optimization depended on various factors, including the regularization type, learner
type, and number of predictors. For more information, see Solver.
See Also
fitrsvm | fitlm | lasso | ridge | fitclinear | predict | kfoldPredict | kfoldLoss | RegressionLinear | RegressionPartitionedLinear
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)