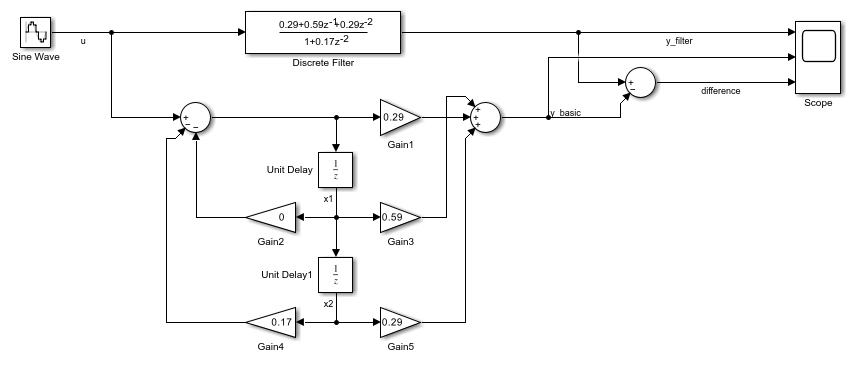
Discrete Filter
Model Infinite Impulse Response (IIR) filters
Libraries:
Simulink /
Discrete
DSP System Toolbox /
Filtering /
Filter Implementations
Description
The Discrete Filter block independently filters each channel of the input
signal with the specified digital IIR filter. You can specify the filter structure as
Direct form I, Direct form I transposed,
Direct form II, or Direct form II transposed.
The block implements static filters with fixed coefficients. You can tune the
coefficients of these static filters.
This block filters each channel of the input signal independently over time. The Input processing parameter allows you to specify how the block treats each element of the input. You can specify treating input elements as an independent channel (sample-based processing), or treating each column of the input as an independent channel (frame-based processing). To perform frame-based processing, you must have a DSP System Toolbox™ license.
The output dimensions equal the input dimensions, except when you specify a matrix of filter taps for the Numerator coefficients parameter. When you do so, the output dimensions depend on the number of different sets of filter taps you specify.
Use the Numerator coefficients parameter to specify the coefficients of the discrete filter numerator polynomial. Use the Denominator coefficients parameter to specify the coefficients of the denominator polynomial of the function. The Denominator coefficients parameter must be a vector of coefficients.
Specify the coefficients of the numerator and denominator polynomials in ascending powers of z-1. The Discrete Filter block lets you use polynomials in z-1 (the delay operator) to represent a discrete system. Signal processing engineers typically use this method. Conversely, the Discrete Transfer Fcn block lets you use polynomials in z to represent a discrete system. Control engineers typically use this method. When the numerator and denominator polynomials have the same length, the two methods are identical.
Specifying Initial States
In Dialog parameters and Input port(s) modes, the block initializes the internal filter states to zero by default, which is equivalent to assuming past inputs and outputs are zero. You can optionally use the Initial states parameter to specify nonzero initial states for the filter delays.
To determine the number of initial state values you must specify, and how to specify them, see the following table on valid initial states and Number of Delay Elements (Filter States). The Initial states parameter can take one of four forms as described in the following table.
Valid Initial States
| Initial state | Examples | Description |
|---|---|---|
|
Scalar |
Each delay element for
each channel is set to |
The block initializes all delay elements in the filter to the scalar value. |
|
Vector |
For a filter with two delay elements: [d1d2] The delay elements for all channels are d1 and d2. |
Each vector element specifies a unique initial condition for a corresponding delay element. The block applies the same vector of initial conditions to each channel of the input signal. The vector length must equal the number of delay elements in the filter (specified in the table Number of Delay Elements (Filter States)). |
|
Vector or matrix | For a three-channel input signal and a filter with two delay elements: [d1d2D1D2d1d2] or
|
Each vector or matrix element specifies a unique initial condition for a corresponding delay element in a corresponding channel:
|
|
Empty matrix |
|
The empty matrix, |
The number of delay elements (filter states) per input channel depends on the filter structure, as indicated in the following table.
Number of Delay Elements (Filter States)
| Filter Structure | Number of Delay Elements Per Channel |
|---|---|
|
|
|
|
|
|
The following tables describe the valid initial states for different sizes of input and different number of channels depending on whether you set the Input processing parameter to frame based or sample based.
Frame-Based Processing
| Input | Number of Channels | Valid Initial States (Dialog Box) | Valid Initial States (Input Port) |
|---|---|---|---|
| 1 |
|
|
| N |
|
|
Sample-Based Processing
| Input | Number of Channels | Valid Initial States (Dialog Box) | Valid Initial States (Input Port) |
|---|---|---|---|
| 1 |
|
|
| N |
|
|
| K × N |
|
|
When the Initial states is a scalar, the block initializes all filter
states to the same scalar value. Enter 0 to initialize all states
to zero. When the Initial states is a vector or a matrix, each
vector or matrix element specifies a unique initial state. This unique state
corresponds to a delay element in a corresponding channel:
The vector length must equal the number of delay elements in the filter,
M = max(number of zeros, number of poles).The matrix must have the same number of rows as the number of delay elements in the filter,
M = max(number of zeros, number of poles). The matrix must also have one column for each channel of the input signal.
The relationship between the initial filter output y1, the initial input u1, and the initial state [x1, x2] is given by the following equation.
where,
b1, b2, and b3 are the numerator coefficients of the discrete filter.
a1, a2, and a3 are the denominator coefficients of the discrete filter.
Examples
Extended Examples
Ports
Input
Output
Parameters
Block Characteristics
More About
Extended Capabilities
Version History
Introduced before R2006aSee Also
Blocks
- Discrete FIR Filter | Allpole Filter (DSP System Toolbox) | Digital Filter Design (DSP System Toolbox)
Functions
dsp.IIRFilter(DSP System Toolbox) |dsp.AllpoleFilter(DSP System Toolbox) |filterDesigner(DSP System Toolbox) |fvtool(Signal Processing Toolbox)
Topics
- Sample- and Frame-Based Concepts (DSP System Toolbox)
- Working with States