freqz
Frequency response of digital filter
Syntax
Description
[
returns the h,w] = freqz(B,A,"ctf",n)n-point frequency response of the digital
filter represented as Cascaded Transfer Functions (CTF) with numerator coefficients B and denominator
coefficients A. (since R2024b)
freqz(___) with
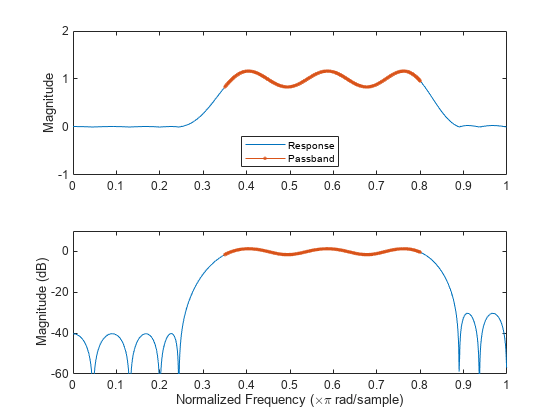
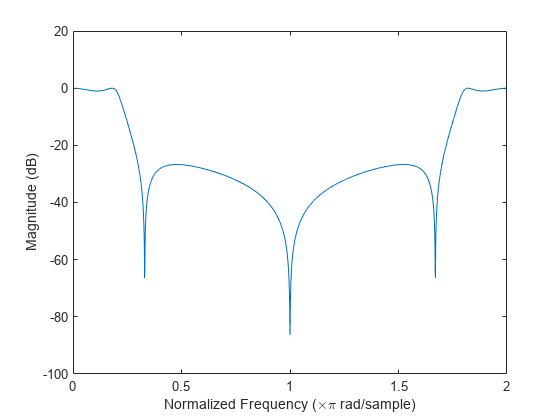
no output arguments plots the frequency response of the filter.
Examples
Input Arguments
Output Arguments
More About
Tips
You can obtain filters in CTF format, including the scaling gain. Use the outputs of digital IIR filter design functions, such as
butter,cheby1,cheby2, andellip. Specify the"ctf"filter-type argument in these functions and specify to returnB,A, andgto get the scale values. (since R2024b)If you have an irreducible multirate filter, use the
freqzmr(DSP System Toolbox) function to analyze the filter in the frequency domain. For more information on irreducible multirate filters, see Overview of Multirate Filters (DSP System Toolbox). (since R2024a)The
freqzmr(DSP System Toolbox) function requires DSP System Toolbox™. (since R2024a)
Algorithms
The frequency response of a digital filter can be interpreted as the transfer function evaluated at z = ejω [1].
freqz determines the transfer function from
the (real or complex) numerator and denominator polynomials you specify
and returns the complex frequency response, H(ejω),
of a digital filter. The frequency response is evaluated at sample
points determined by the syntax that you use.
freqz generally uses an FFT algorithm to compute the frequency response
whenever you do not supply a vector of frequencies as an input argument. It computes the
frequency response as the ratio of the transformed numerator and denominator
coefficients, padded with zeros to the desired length.
When you do supply a vector of frequencies as input, freqz evaluates the
polynomials at each frequency point and divides the numerator response by the
denominator response. To evaluate the polynomials, the function uses Horner's
method.
References
[1] Oppenheim, Alan V., and Ronald W. Schafer, with John R. Buck. Discrete-Time Signal Processing. 2nd Ed. Upper Saddle River, NJ: Prentice Hall, 1999.
[2] Lyons, Richard G. Understanding Digital Signal Processing. Upper Saddle River, NJ: Prentice Hall, 2004.