Find and Remove Trends
Find and remove polynomial or periodic trends from data in the Live Editor
Description
The Find and Remove Trends task lets you interactively identify polynomial or periodic trends in data and return or remove them. The task automatically generates MATLAB® code for your live script. For more information about Live Editor tasks generally, see Add Interactive Tasks to a Live Script.
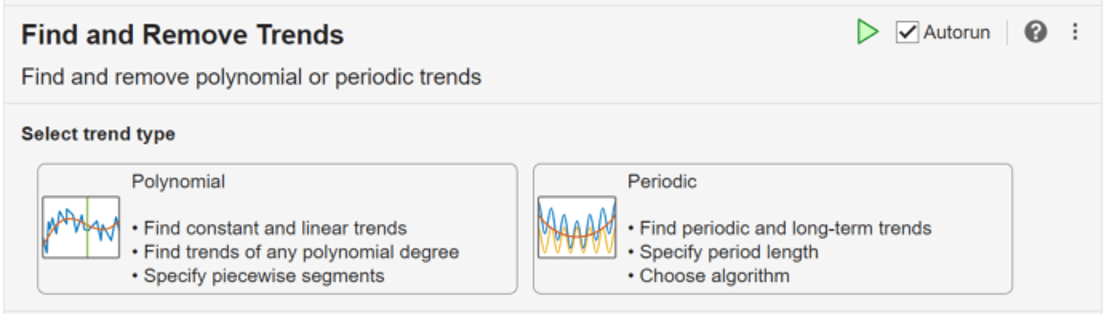
Using this task, you can:
Identify a polynomial trend in data.
Choose the degree of the polynomial trend to remove from data.
Dynamically arrange breakpoints to define piecewise segments of the data.
Specify continuity constraints.
Visualize and return the computed trends and data with the trends removed.
Identify long-term and periodic, seasonal, or oscillatory trends in data.
Choose the Singular Spectrum Analysis (SSA) or Seasonal Trend Decomposition Using Loess (STL) algorithm to find trends in the data.
Specify the number of periodic trends and lag window when the periods of trends are unknown.
Specify period lengths when the periods of trends are known.
Visualize and return the computed trends and data with the trends removed.
Related Functions
Find and Remove Trends generates code that uses the
detrend and trenddecomp
functions.
Open the Task
To add the Find and Remove Trends task to a live script in the MATLAB Editor:
On the Live Editor tab, select Task > Find and Remove Trends.
In a code block in the script, type a relevant keyword, such as
find,remove,detrend,trenddecomp,stl, orssa. SelectFind and Remove Trendsfrom the suggested command completions. Then, select the trend type. For some keywords, the task automatically updates one or more corresponding parameters.
Examples
Interactively identify and remove a linear trend in array data with the Find and Remove Trends task in the Live Editor.
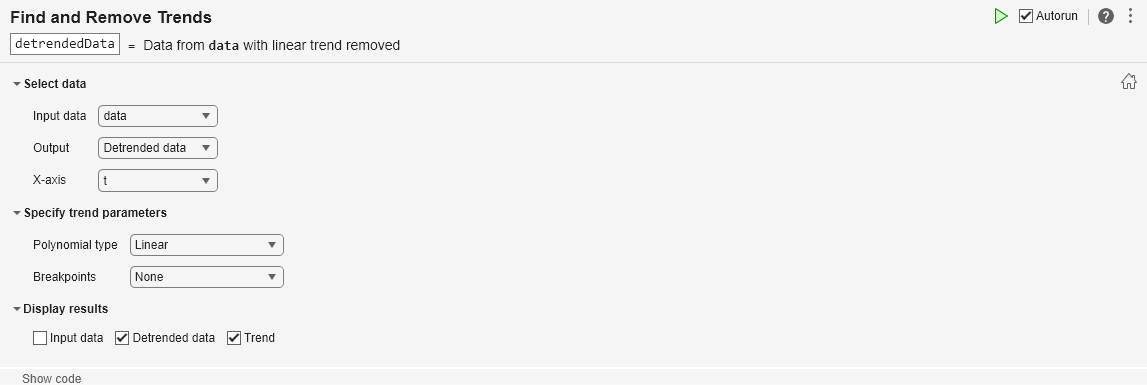
Create a vector x containing some fluctuation. Create a plot to visualize the data.
t = 0:8; trend = 2*t+5; sig = [0 1 -2 1 0 1 -2 1 0]; data = sig + trend; plot(t,data)
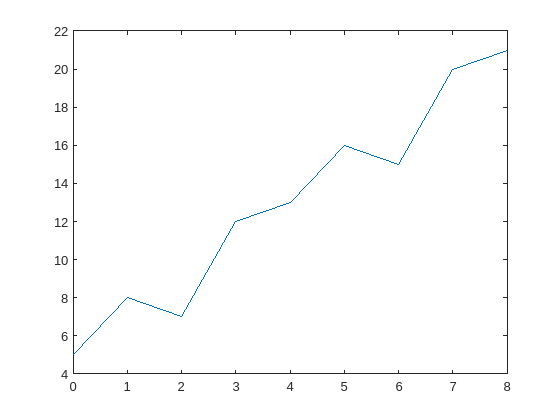
Add the Find and Remove Trends task to the live script. Because the data has a polynomial trend, choose the Polynomial trend type.
Remove the polynomial trend from the data. Select data as the input data and Detrended data as the output to return. Alternatively, you can use the Output field to return the trend. Select t as the x-axis values associated with the input data. Identify a linear trend by specifying the polynomial type as Linear.
Display the resulting trend and the detrended data in a stacked plot.

Interactively identify and remove a piecewise polynomial trend in array data using the Find and Remove Trends task in the Live Editor.
A polynomial trend is a trend that best describes fluctuating data. A polynomial trend is used when your data both increases and decreases in value, and the degree of the polynomial trend increases as the data fluctuates.
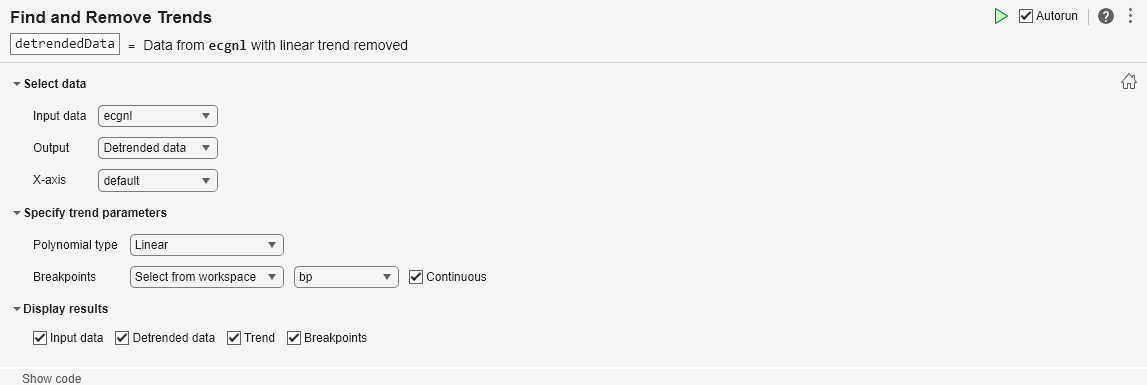
Consider an electrocardiogram (ECG) signal that shows a pattern not intrinsic to the data that must be removed. Load the signal ecgnl using the sample file ecgSignals.mat and plot the signal.
load("ecgSignals.mat","ecgnl") plot(ecgnl) title("ECG Signals with Trends") xlabel("Sample") ylabel("Voltage (mV)")

Then, eliminate the nonlinear trend. Add the Find and Remove Trends task to the live script. Because the data has a polynomial trend, choose the Polynomial trend type.
Operate on the signal by selecting ecgnl as the input data. Select Detrended data as the output. The default x-axis values are the sample numbers. Because the wander of the heart rhythm does not occur with consistent frequency, identify a piecewise trend by specifying a vector of breakpoints in the sample data. Alternatively, you can select the breakpoints from a plot.
bp = [160 660 1160 1660];
Then, choose a custom polynomial type and specify the polynomial degree as 5. The resulting visualization displays the input data, piecewise polynomial trend, and the data with the trend removed. The detrended data is returned in detrendedData and has the same size as ecgnl. Alternatively, to return the trend, use the Output field.

Interactively decompose array data into its long-term trend, two periodic trends, and remainder using the seasonal trend decomposition using loess (STL) algorithm with the Find and Remove Trends task in the Live Editor.
Create a variable data that contains a long-term trend, two seasonal trends with different periods, and a noise component. Create a plot to visualize the data.
t = (1:200)'; trend = 0.001*(t-100).^2; period1 = 20; period2 = 30; seasonal1 = 2*sin(2*pi*t/period1); seasonal2 = 0.75*sin(2*pi*t/period2); noise = 2*(rand(200,1) - 0.5); data = trend + seasonal1 + seasonal2 + noise; plot(data)
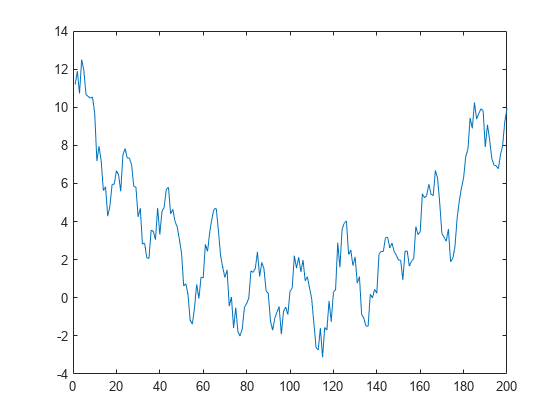
Add the Find and Remove Trends task to the live script. Because the data has a recurring, periodic trend, choose the Periodic trend type.
Decompose the data into its trend components by selecting data as the input data and All trends as the output to return. Because the periods of the seasonal trends in the data are known, choose the STL algorithm and specify the known period lengths as 20 and 30 data points.
Display the input data and the resulting long-term trend, two periodic trends, and remainder in a stacked plot. The Live Editor task returns the identified trends in arrays longterm and periodic. Alternatively, to return the detrended data, use the Output field to specify which trend types to remove.
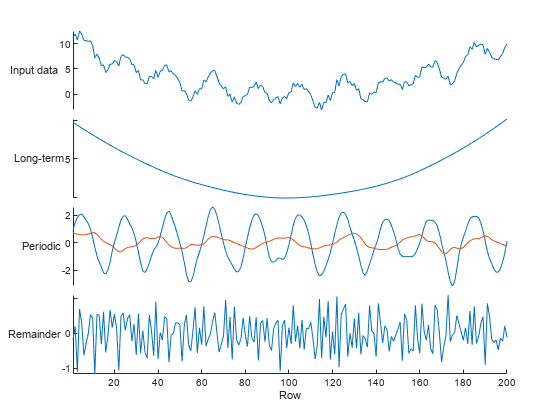
Interactively identify and return periodic trends using the singular spectrum analysis (SSA) algorithm with the Find and Remove Trends task in the Live Editor.
Consider a timetable of monthly international airline passenger totals from 1949 to 1960. Load the timetable using the sample file Data_Airline.mat and plot the passenger data.
load("Data_Airline.mat","DataTimeTable"); plot(DataTimeTable,"Time","PSSG") title("Passenger Data")

Notice that the timetable is irregularly spaced. The Find and Remove Trends task requires that the input timetable is regularly spaced.
isregular(DataTimeTable.Time)
ans = logical
0
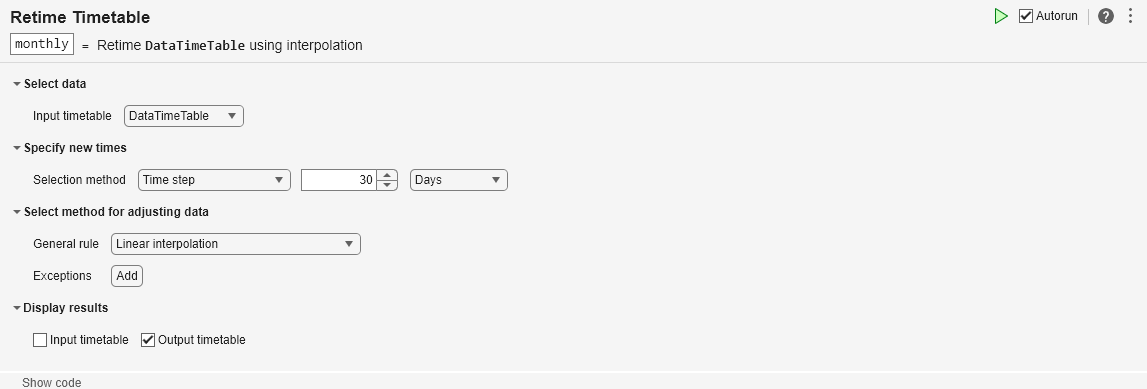
Make the timetable regular by resampling using the Retime Timetable task in the Live Editor. Interpolate the data onto a regular time vector with a time step of 30 days and return the resampled data in a timetable named monthly.
monthly=147×1 timetable
Time PSSG
___________ ______
01-Jan-1949 112
31-Jan-1949 117.81
02-Mar-1949 131.9
01-Apr-1949 129
01-May-1949 121
31-May-1949 134.55
30-Jun-1949 147.57
30-Jul-1949 148
29-Aug-1949 137.16
28-Sep-1949 120.7
28-Oct-1949 105.94
27-Nov-1949 116.13
27-Dec-1949 115.48
26-Jan-1950 123.87
25-Feb-1950 138.86
27-Mar-1950 135.97
⋮
isregular(monthly.Time)
ans = logical
1
The airline passenger data shows an increase in the seasonal variance over time. Because the Find and Remove Trends task analyzes the series using additive decomposition models, apply a log transformation to the data.
monthly.PSSGLog = log(monthly.PSSG);
Then, identify periodic trends in the passenger data by adding the Find and Remove Trends task to the live script. Because the data has a recurring, periodic trend, choose the Periodic trend type.
Operate on the passenger totals by specifying the input data as the PSSGLog variable of monthly. Because the periods of the seasonal trends in the data are unknown, choose the SSA algorithm. Increase the number of periodic trends until the baseline of the remainder is flat.
Display the input data and the resulting long-term trend, four periodic trends, and remainder in a stacked plot. The Live Editor task returns the identified trends in the array trends. Alternatively, to return the detrended data, use the Output field to specify which trend types to remove.

Related Examples
Parameters
Polynomial Trends
This task operates on input data contained in a vector, matrix, multidimensional
array, table, or timetable. The data can be of type single or
double.
For table or timetable input data, this task operates on each table variable
separately. To operate on all variables with type single or
double, select All supported variables.
To choose which single or double variables to
operate on, select Specified variables.
Periodic Trends
This task operates on input data contained in a vector, table, or timetable. The
data can be of type single or double. For
timetable input data, the vector of row times must be regularly spaced.
For table or timetable input data, this task operates on each table variable
separately. To operate on all variables with type single or
double, select All supported variables.
To choose which single or double variables to
operate on, select Specified variables.
Tips
If your data has seasonal variation that is proportional to the level of the time series, use a
logtransformation on the data before looking for periodic trends.
Algorithms
For a polynomial trend, use the Breakpoints field to specify the location of breakpoints. A breakpoint is a point in the range of x that separates intervals and identifies a piecewise trend consisting of multiple subfunctions. A piecewise trend can be continuous, where the limits of subfunctions as they approach a breakpoint are equal, or discontinuous, where the limits are not equal.
For a periodic trend, use the Algorithm field to specify SSA. SSA is an additive decomposition model used for regularly spaced time series when the periods of recurring, periodic trends are unknown. The algorithm uses singular value decomposition (SVD) to decompose a time series into a specified number of periodic trends. A lag value determines the size of the matrix on which the SVD is computed. Larger lag window values typically result in more separation of the trends.
An additive decomposition model decomposes time series data such that A =
LT+ST+R, where LT is the long-term trend in the data,
ST is the seasonal, or oscillatory, trend (or trends), and
R is the remainder.
For a periodic trend, use the Algorithm field to specify STL. STL is an additive decomposition model used for regularly spaced time series when the periods of recurring, periodic trends are known. The algorithm uses loess (locally weighted smoothing) to decompose a time series into periods of specified lengths.
An additive decomposition model decomposes time series data such that A =
LT+ST+R, where LT is the long-term trend in the data,
ST is the seasonal, or oscillatory, trend (or trends), and
R is the remainder.
Version History
Introduced in R2019bIn addition to identifying polynomial trends, you can now interactively identify periodic trends for regularly spaced input data. Select the trend type as Periodic, and choose the SSA or STL algorithm.
You can also return polynomial and periodic trend data, in addition to the detrended
data, using this Live Editor task. Specify the Output as
Trends.
Previously, this task identified only polynomial trends and returned only the detrended data.
To reflect the enhanced functionality, this task is now named Find and Remove Trends. Previously, this task was named Remove Trends.
Simultaneously plot multiple table variables in the display of this Live Editor task. For table or timetable data, to visualize all selected table variables at once in a tiled chart layout, set the Variable to display field.
Append input table variables with table variables containing detrended data. For table or timetable input data, to append the detrended data, set the Output format field.
This Live Editor task does not run automatically if the input data is large. In previous releases, the task always ran automatically for inputs of any size. If the inputs have a large number of elements, then the code generated by this task can take a noticeable amount of time to run (more than a few seconds).
When a task does not run automatically, the Autorun indicator is disabled. You can either run the task manually when needed or choose to enable the task to run automatically.
This Live Editor task can operate on multiple table variables at the same time. For table
or timetable input data, to operate on multiple variables, select All supported
variables or Specified variables. Return all of
the variables or only the modified variables, and specify which variable to
visualize.
See Also
Functions
Live Editor Tasks
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)