Analyze Time Series Data Using Econometric Modeler

The Econometric Modeler app is an interactive tool for analyzing univariate or multivariate time series data. The app is well suited for visualizing and transforming data, performing statistical specification and model identification tests, fitting models to data, and iterating among these actions. When you are satisfied with a model, you can export it to the MATLAB^® Workspace to forecast future responses or for further analysis. You can also generate code or a report from a session.

Start Econometric Modeler by entering econometricModeler at the MATLAB command line, or by clicking Econometric Modeler under Computational Finance in the apps gallery (Apps tab on the MATLAB Toolstrip).

The following workflow describes how to find a model with the best in-sample fit to time series data using Econometric Modeler. The workflow is not a strict prescription—the steps you implement depend on your goals and the model type. You can easily skip steps and iterate several steps as needed. The app is well suited to the Box-Jenkins approach to time series model building [1].

1. Prepare data for Econometric Modeler — For a response variable, or select multiple response variables for a multivariate analysis, to analyze and from which to build a predictive model. Optionally, select explanatory variables to include in the model.

   Note

   You can import only one variable from the MATLAB Workspace into Econometric Modeler. Therefore, at the command line, you must synchronize and concatenate multiple series into one variable.

2. Import time series variables — Import Data into Econometric Modeler from the MATLAB Workspace or a MAT-file. After importing data, you can adjust variable properties or the presence of variables.

3. Perform exploratory data analysis — View the series in various ways, stabilize the series by transforming them, and detect time series properties by performing statistical tests.

   • Visualize time series data — Supported plots include time series plots and correlograms (for example, the autocorrelation function (ACF)).

   • Perform specification and model identification hypothesis tests — Test series for stationarity, heteroscedasticity, autocorrelation, and collinearity or cointegration among multiple series. For ARIMA and GARCH models, this step can include determining the appropriate number of lags to include in the model. Supported tests include the augmented Dickey-Fuller test, Engle's ARCH test, the Ljung-Box Q-test, Belsley collinearity diagnostics, and the Johansen cointegration test.

   • Transform time series — Supported transformations include the log transformation and seasonal and nonseasonal differencing.

4. Fit candidate models to the data — Choose model parametric forms for univariate or multivariate response series based on the exploratory data analysis or dictated by economic theory. Then, estimate the model. Supported univariate models include seasonal and nonseasonal conditional mean (for example, ARIMA), conditional variance (for example, GARCH), and multiple linear regression models (optionally containing ARMA errors). Supported multivariate models include vector autoregression (VAR) and vector error-correction (VEC) models.

5. Conduct goodness-of-fit checks — Ensure that the model adequately describes the data by performing residual diagnostics.

   • Visualize the residuals to check whether they are centered on zero, normally distributed, homoscedastic, and serially uncorrelated. Supported plots include quantile-quantile and ACF plots.

   • Test the residuals for homoscedasticity and autocorrelation. Supported tests include the Ljung-Box Q-test and Engle's ARCH test on the squared residuals.

6. Find the model with the best in-sample fit — Estimate multiple models within the same family, and then choose the model that yields the minimal fit statistic, for example, Akaike information criterion (AIC).

7. Export session results — After you find a model or models that perform adequately, summarize the results of the session. The method you choose depends on your goals. Supported methods include:

   • Export variables — Econometric Modeler exports selected variables to the MATLAB Workspace. If a session in the app does not complete your analysis goal, such as forecasting responses, then you can export variables (including estimated models) for further analysis at the command line.

   • Generate a function — Econometric Modeler generates a MATLAB plain text or live function that returns a selected model given the imported data. This method helps you understand the command-line functions that the app uses to create predictive models. You can modify the generated function to accomplish your analysis goals.

   • Generate a report — Econometric Modeler produces a document, such as, a PDF, describing your activities on selected variables or models. This method provides a clear and convenient summary of your analysis when you complete your goal in the app.

Prepare Data for Econometric Modeler App

You can import only one variable from the MATLAB Workspace into Econometric Modeler. Therefore, before importing data, concatenate the response series and any predictor series into one variable.

Econometric Modeler supports these variable data types.

• MATLAB timetable — Variables must be double-precision numeric vectors. A best practice is to import your data in a timetable because Econometric Modeler:

  • Names variables by using the names stored in the VariableNames field of the Properties property.

  • Uses the time variable values as tick labels for any axis that represents time. Otherwise, tick labels representing time are indices.

  • Enables you to overlay recession bands on time series plots (see recessionplot)

  For more details on timetables, see Create Timetables.

• MATLAB table — Variables must be double-precision numeric vectors. Variable names are the names in the VariableNames field of the Properties property.

• Numeric vector or matrix — For a matrix, each column is a separate variable named variableNamej, where j is the corresponding column.

Regardless of variable type, Econometric Modeler assumes that rows correspond to time points (observations).

Import Time Series Variables

The data set can exist in the MATLAB Workspace or in a MAT-file that you can access from your machine.

• To import a data set from the Workspace, on the Econometric Modeler tab, in the Import section, click . In the Import Data dialog box, click the check box in the Import? column for the variable containing the data, and then click Import. All variables in the Workspace of the supported data type appear in the dialog box, but you can choose one only.

• To import data from a MAT-file, in the Import section, click Import, then select Import From MAT-file. In the Select a MAT-file dialog box, browse to the folder containing the data set, then double-click the MAT-file.

After you import data, Econometric Modeler performs all the following actions.

• The name of each variable (column) in the data set appears in the Time Series pane.

• The value of the variable selected in the Time Series pane appears in the Preview pane.

• A time series plot including all variables appears in the Time Series Plot(VariableName) figure window, where VariableName is the name of one of the variables in the Time Series pane.

You can interact with the variables in the Time Series pane in several ways.

• To select a variable to perform a statistical test or create a plot, for example, click the variable in the Time Series pane. If you double-click the variable instead, then the app also plots it in a separate time series plot.

• To open, delete, or export a variable, right-click it in the Time Series pane. Then, from the context menu, choose the desired action.

• To select or operate on multiple time series simultaneously, press Ctrl and click each variable you want to use.

Consider importing the data in the Data_USEconModel MAT-file.

1. At the command line, load the data into the Workspace.

   load Data_USEconModel

2. In Econometric Modeler, in the Import section of the Econometric Modeler tab, click . The Import Data dialog box appears.

3. Data_USEconModel stores several variables. Data, DataTable, and DataTimeTable contain the same data, but DataTable is a table, and DataTimeTable is a timetable. Import DataTimeTable by selecting the corresponding Import? check box, then clicking Import.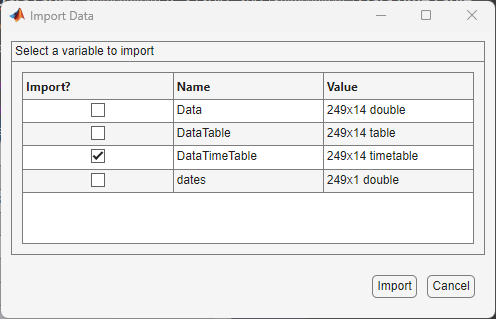

   

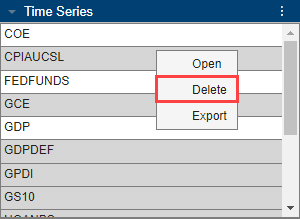
All variables in DataTimeTable appear in the Time Series pane. Suppose that you want to retain COE, FEDFUNDS, and GDP only. Select all other variables, right-click one of them, and select Delete.

After working in the app, you can import another data set. After you click Import, Econometric Modeler displays the following dialog box.

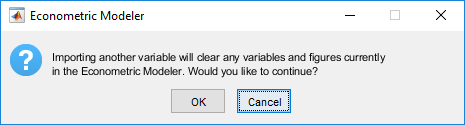
If you click OK, then Econometric Modeler deletes all variables from the Time Series and Models panes, and closes all documents in the right pane.

Perform Exploratory Data Analysis

An exploratory data analysis includes determining characteristics of your variables and relationships between them, with the formation of a predictive model in mind. For time series data, identify series that grow exponentially, contain trends, or are nonstationary, and then transform them appropriately. For ARIMA models, to identify the model form and significant lags in the serial correlation structure of the response series, use the Box-Jenkins methodology [1]. If you plan to create GARCH models, then assess whether the series contain volatility clustering and significant lags. For multiple regression models, identify collinear predictors and those predictors that are linearly related to the response. For multivariate models, in addition to univariate analyses, you can test whether series are cointegrated.

For time series data analysis, an exploratory analysis usually includes iterating among visualizing the data, performing statistical specification and model identification tests, and transforming the data.

Visualizing Time Series Data

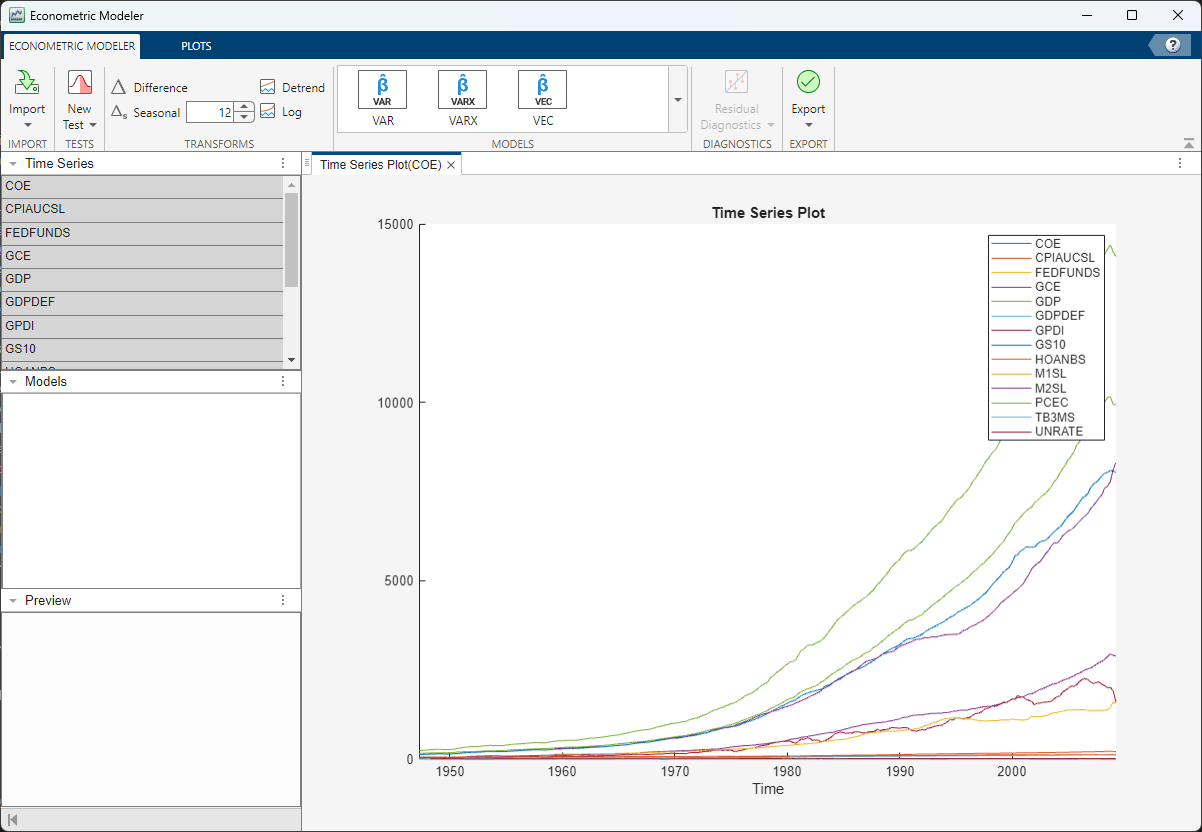
After you import a data set, Econometric Modeler selects all variables in the imported data and displays a time series plot of them in the right pane by default. For example, after you import DataTimeTable in the Data_USEconModel data set, the app displays this time series plot.

To create your own time series plot:

1. In the Time Series pane, select the appropriate number of series for the plot.

2. Click the Plots tab in the toolstrip.

3. Click the button for the type of plot you want.

Econometric Modeler supports the following time series plots.

Plot	Goals
Time series or	Identify missing values or outliers. Identify series that grow exponentially or that contain a trend. Identify nonstationary series. Identify series that contain volatility clustering. Compare two series with different scales in the same plot (Y-Y Axis). Compare multiple series with similar scales in the same plot.
Autocorrelation function (ACF)	Identify series with serial correlation. Determine whether an AR model is appropriate. Identify significant MA lags for model identification.
Partial ACF (PACF)	Identify series with serial correlation. Determine whether an MA model is appropriate. Identify significant AR lags for model identification.
Correlations	Inspect variable distributions. Identify variables with linear relationships pairwise.

You can interact with an existing plot by:

• Right-clicking it

• Using the plot buttons that appear when you pause on the plot

• Using the options on the figure window

Supported interactions vary by plot type.

• Save a figure — Right-click the figure, then select Export. Save the figure that appears.

• Add or remove time series in a plot — Right-click the figure, point to Show Time Series menu, then select the time series to add or remove.

• Plot recession bands — Right-click a time series plot, then select Show Recessions.

• Show grid lines — Pause on the figure, then click .

• Toggle legend — Pause on the figure, then click .

• Pan — Pause on the figure, then click . For more details on panning, see Zoom, Pan, and Rotate Data.

• Zoom — Pause on the figure. To zoom in, click . To zoom out, click . For more details, see Zoom, Pan, and Rotate Data.

• Restore view — To return the plot to its original view after you pan or zoom, pause on the figure, then click .

For serial correlation function plots, additional options exist in the ACF or PACF tabs. You can specify the:

• Number of lags to display

• Number of standard deviations for the confidence bands

• MA or AR order in which the theoretical ACF or PACF, respectively, is effectively zero

Econometric Modeler updates the plot in real time as you adjust the parameters.

As you explore your data, plots and computation results accumulate in the right pane under tabs. You can customize the display of the documents in the right pane to, for example, view multiple plots simultaneously, by performing any of the following actions:

• Orient the plot tabs by dragging them into different sections of the right pane. As you drag a plot, the app highlights possible sections in which to place it. To undo the last document or figure window positioning, pause on the dot located in the middle of the partition, then click when it appears.

• Click the Document Actions button on the upper-right corner of the document. Options include:

  • Tile All — Choose a layout for multiple plots.

  • Tab Position — Select where to display the figure tab.

Consider an ARIMA model for the effective federal funds rate (FEDFUNDS). To identify the model characteristics (for example, the number of AR or MA lags), plot the time series, ACF, and PACF side-by-side.

1. In the Time Series pane, double-click FEDFUNDS.

2. Add recession bands to the plot by right-clicking the plot in the Time Series Plot(FEDFUNDS) figure window, then selecting Show Recessions.

3. On the Plots tab, click ACF.

4. Click PACF.

5. Click the Time Series Plot(FEDFUNDS) figure window and drag it to the left side of the right pane. Click the PACF(FEDFUNDS) figure window and drag it to the bottom right of the pane.

   

The ACF dies out slowly and the PACF cuts off after the first lag. The behavior of the ACF suggests that the time series must be transformed before you choose on the form of the ARIMA model.

In the right pane, observe the dot in the middle of the horizontal partition between the correlograms (below the Lag x axis label of the ACF). To undo this correlogram positioning, that is, separate the correlograms by tabs, pause on the dot and click when it appears.

Performing Specification and Model Identification Hypothesis Tests

You can perform hypothesis tests to confirm time series properties that you obtain visually or test for properties that are difficult to see. Econometric Modeler enables you to run tests multiple times with parameter settings.

Econometric Modeler supports these tests for univariate series.

Test	Hypotheses
Augmented Dickey-Fuller	H0: Series has a unit root. H1: Series is stationary. For details on the supported parameters, see adftest.
Kwiatkowski, Phillips, Schmidt, Shin (KPSS)	H0: Series is trend stationary. H1: Series has a unit root. For details on the supported parameters, see kpsstest.
Leybourne-McCabe	H0: Series is a trend stationary AR(p) process. H1: Series is an ARIMA(p,1,1) process. To specify p, adjust the Number of Lags parameter. For details on the supported parameters, see lmctest.
Phillips-Peron	H0: Series has a unit root. H1: Series is stationary. For details on the supported parameters, see pptest.
Variance ratio	H0: Series is a random walk. H1: Series is not a random walk. For details on the supported parameters, see vratiotest.
Engle's ARCH	H0: Series exhibits no conditional heteroscedasticity (ARCH effects). H1: Series is an ARCH(p) model, with p > 0. To specify p, adjust the Number of Lags parameter. For details on the supported parameters, see archtest.
Ljung-Box Q-test	H0: Series exhibits no autocorrelation in the first m lags, that is, corresponding coefficients are jointly zero. H1: Series has at least one nonzero autocorrelation coefficient ρj, j ∈ {1,…,m}. To specify m, adjust the Number of Lags parameter. For details on the supported parameters, see lbqtest.

Note

Before conducting tests, Econometric Modeler removes leading and trailing missing values (NaN values) in the series. Engle's ARCH test does not support missing values within the series, that is, NaN values preceded and succeeded by observations.

The stationarity test results suggest whether you should transform a series to stabilize it, and which transformation is appropriate. For ARIMA models, stationarity test results suggest whether to include degrees of integration. Engle's ARCH test results indicate whether the series exhibits volatility clustering and suggests lags to include in a GARCH model. Ljung-Box Q-test results suggest how many AR lags are required in an ARIMA model.

To perform a univariate test in Econometric Modeler:

1. Select a variable in the Time Series pane.

2. On the Econometric Modeler tab, in the Tests section, click New Test.

3. In the test gallery, click the test you want to conduct. A new tab for the test type appears in the toolstrip, and a new document for the test results appears in the right pane.

4. On the test type tab, in the Parameters section, adjust parameters for the test. For example, consider performing an Engle's ARCH test. On the ARCH tab, in the Parameters section, select the number of lags in the test statistic using the Number of Lags spin box, or the significance level (that is, the value of α) using the Significance Level spin box.

   

5. On the test-type tab, in the Tests section, click Run Test. The test results, including whether to reject the null hypothesis, the p-value, and the parameter settings, appear in a new row in the Results table of the test results document. If the null hypothesis has been rejected, then the app highlights the row in yellow.

If you run multiple tests on a particular series, the results of each test appear as a new row in the Results table. To remove a row from the Results table, select the corresponding check box in the Select column, then click Clear Tests in the test-type tab.

Note

Multiple testing inflates the false discovery rate. One conservative way to maintain an overall false discovery rate of α is to apply the Bonferroni correction to the significance level of each test. That is, for a total of t tests, set Significance Level value to α/t.

Econometric Modeler supports these tests and diagnostics for multiple series.

Tests and Diagnostics	Description
Belsley Collinearity Diagnostics	For details on the supported parameters and results, see collintest.
Engle-Granger	H0: The series do not exhibit cointegration. H1: The series exhibit cointegration. For details on the supported parameters, see egcitest.
Johansen	For a specified cointegration rank r: H0: The series exhibit at most rank r cointegration. H1: The series exhibit cointegration with rank greater than r. For details on the supported parameters, see jcitest.

To diagnose multiple series in Econometric Modeler:

1. Select at least two variables in the Time Series pane.

2. On the Econometric Modeler tab, in the Tests section, click New Test.

3. In the tests gallery, select the diagnostics you want to run. A new tab for the diagnostic appears in the toolstrip, and a new document for the results appears in the right pane.

4. On the tab for the diagnostic, you can adjust parameters for the diagnostic in the appropriate section. For example, consider conducting an Engle-Granger cointegration test on the selected series. In the tests gallery, select Engle-Granger Test. On the EGCI tab, in the Parameters section, select the cointegration regression form by using the Cointegration Regression Form list and select the test to conduct on the regression residuals by using the Residual Regression Form list.

   

For example, consider a predictive model containing Canadian inflation and interest rates as predictor variables. Determine whether the variables are collinear. The Data_Canada data set contains the time series.

1. Import the DataTimeTable variable in the Data_Canada data set into Econometric Modeler (see Import Time Series Variables). The time series plot appears in the right pane.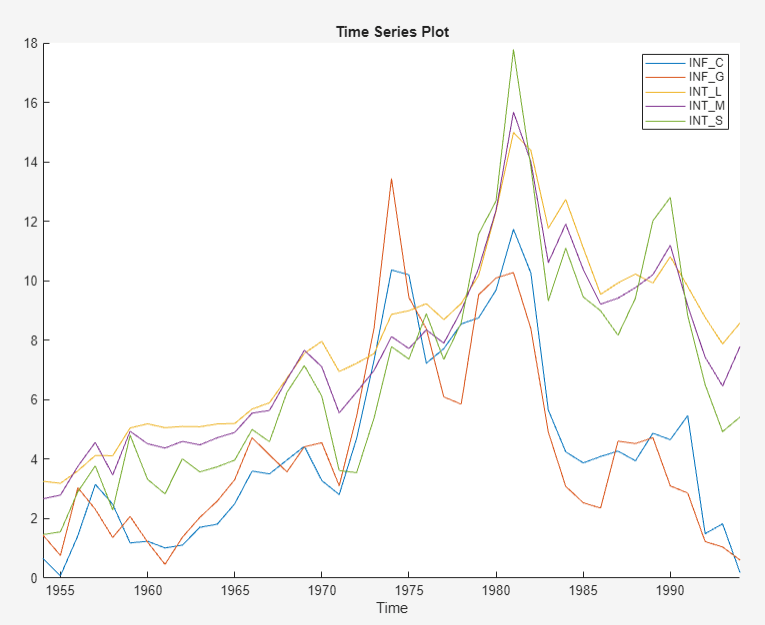

   

   All series appear to contain autocorrelation. Although you should remove autocorrelation from predictor variables before creating a predictive model, this example proceeds without removing autocorrelation.

2. In the Tests section, click New Test. In the Collinearity section, click Belsley Collinearity Diagnostics.

   Econometric Modeler creates a new tab for the Belsley collinearity diagnostics in the toolstrip, and a it creates a new document for the results in the right pane. The results contains a table of the singular values, condition indices, and the variance-decomposition proportions for each series. Rows Econometric Modeler highlights in yellow have a condition index greater than the tolerance specified by the Condition Index parameter value (default is 30) in the Tolerances section of the Collinearity tab. The columns of the table labeled with series names form the matrix of variance-decomposition proportions. Those series with variance-decomposition proportion greater than the tolerance specified by the Variance-Decompoosition Proportion parameter value (default is 0.5) in the highlighted row exhibit multicollinearity.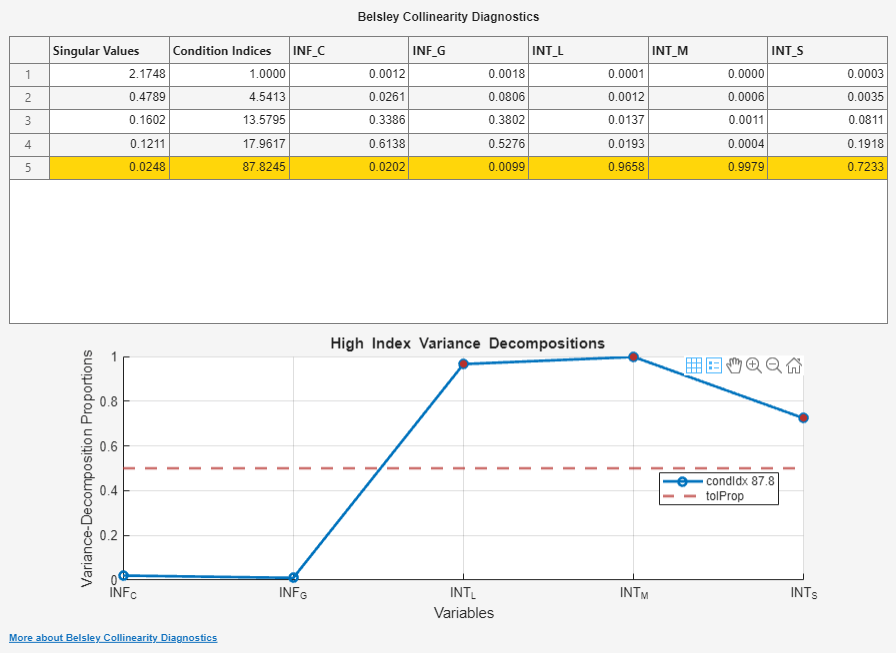

   

   Because their variance-decomposition proportions are above the tolerance (default tolerance is 0.5) for the condition index, the collinear predictors are INT_L, INT_M, and INT_S.

3. You can add or remove time series from the diagnostics. For example, remove the inflation rates from the diagnostics by performing the following procedure.

   1. In the test-results document, right-click the Results table or plot.

   2. Point to Show Time Series. A list of all variables appears.

   3. Remove the inflation rate series INF_C and INF_G from the diagnostics by deselecting the corresponding check boxes. As you deselect series, Econometric Modeler recomputes the results based on the selected series.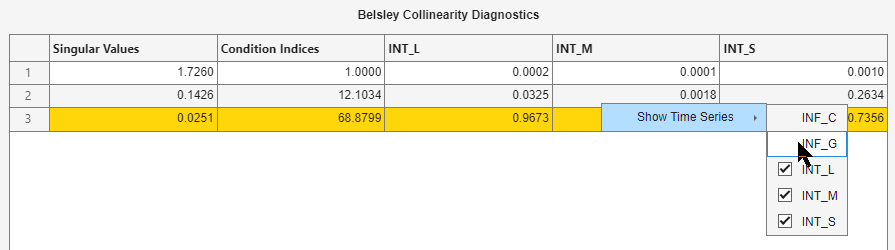

      

For more details on the Belsley collinearity diagnostics results and multicollinearity, see collintest and Time Series Regression II: Collinearity and Estimator Variance.

Transforming Time Series

The Box-Jenkins methodology [1] for ARIMA model selection assumes that the response series is stationary, and spurious regression models can result from a model containing nonstationary predictors and response variables (for more details, see Time Series Regression IV: Spurious Regression). To stabilize your series, Econometric Modeler supports these transformations in the Transforms section of the Econometric Modeler tab.

Transformation	Use When Series ...	Notes
Log	Has an exponential trend or variance that grows with its levels	All values in the series must be positive.
Linear detrend	Has a linear deterministic trend that can be identified using least squares	When Econometric Modeler detrends the series, it ignores leading or trailing missing (NaN) values. If any missing values occur between observed values, then the app returns a vector of NaN values with length equal to the series.
First-order difference	Has a stochastic trend	Econometric Modeler prepends the differenced series with a NaN value. This action ensures that the differenced series has the same length and time base as the original series.
Seasonal difference	Has a seasonal, stochastic trend	You can specify the period in a season using the spin box. For example, 12 indicates a monthly seasonal transformation. Econometric Modeler prepends the differenced series with nan(period,1), where period is the specified period in a season. This action ensures that the differenced series has the same length and time base as the original series.

For more details, see Data Transformations.

To transform a variable, select the variable in the Time Series pane, then click a transformation. After you transform a series, a new variable representing the transformed series appears in the Time Series pane. Also, Econometric Modeler plots and selects the new variable. To create the variable name, the app appends the transformation name to the end of the variable name. You can rename the transformed variable by clicking it twice in the Time Series to select the text of the variable name, and then entering the new name. You can select multiple series by pressing Ctrl and clicking each series, and then apply the same transformation to the selected series simultaneously. The app creates new variables for each series, appends the transformation name to the end of each transformed variable name, and plots the transformed variables in the same figure.

For example, suppose that the GDP series in Data_USEconModel has an exponential trend and a stochastic trend. Stabilize the GDP by applying the log transformation and then applying the second difference.

1. Import the DataTimeTable variable in the Data_USEconModel data set into the Econometric Modeler (see Import Time Series Variables).

2. In the Time Series pane, select GDP.

3. On the Econometric Modeler tab, in the Transforms section, click Log. The app creates a variable named GDPLog, which appears in the Time Series pane, and displays a plot for the time series.

4. In the Transforms section, click Difference. The app creates a variable named GDPLogDiff and displays a plot for the time series.

5. In the Transforms section, click Difference. The app creates a variable called GDPLogDiffDiff and displays a plot for the time series.

GDPLogDiffDiff is the stabilized GDP.

Fitting Models to Data

The results of an exploratory data analysis can suggest several candidate models. To choose a model, in the Time Series pane, select the time series for the response. On the Econometric Modeler tab, in the Models section, click a model or click one in the models gallery. Econometric Modeler allows you to select only those models that are appropriate for the number of the selected response series. After you select a model, you configure it for estimation.

Econometric Modeler supports the following models.

Model	Response	Type
Conditional mean: ARMA/ARIMA Models section	Univariate	Stationary autoregressive (AR) For details, see What Are Autoregressive Models?, arima, and estimate.
	Univariate	Stationary moving average (MA) For details, see What Are Moving Average Models?, arima, and estimate.
	Univariate	Stationary ARMA For details, see What Are Autoregressive Moving Average Models?, arima, and estimate.
	Univariate	Nonstationary, integrated ARMA (ARIMA) For details, see What Are ARIMA Models?, arima, and estimate.
	Univariate	Seasonal (Multiplicative) ARIMA (SARIMA) For details, see What Are Multiplicative ARIMA Models?, arima, and estimate.
	Univariate	ARIMA including exogenous predictors (ARIMAX) For details, see What Are ARIMA Models That Include Exogenous Covariates?, arima, and estimate.
	Univariate	Seasonal ARIMAX For details, see arima and estimate.
Conditional variance: GARCH Models section	Univariate	Generalized autoregressive conditional heteroscedastic (GARCH) For details, see GARCH Model, garch, and estimate.
	Univariate	Exponential GARCH (EGARCH) For details, see EGARCH Model, egarch, and estimate.
	Univariate	Glosten, Jagannathan, and Runkle (GJR) For details, see GJR Model, gjr, and estimate.
Multiple linear regression: Regression Models section	Univariate	Multiple linear regression For details, see Time Series Regression I: Linear Models, LinearModel, and fitlm.
	Univariate	Regression model with ARMA errors For details, see Regression Models with Time Series Errors, regARIMA, and estimate.
Vector Autoregression Models: Multivariate Models section	Multivariate	Stationary vector autoregression (VAR) For details, see Vector Autoregression (VAR) Models and varm.
	Multivariate	VAR including exogenous variable (VARX) For details, see Vector Autoregression (VAR) Models and varm.
	Multivariate	Vector error-correction (VEC) or cointegrated VAR For details, see vecm.

For univariate conditional mean model estimation, SARIMA and SARIMAX are the most flexible models. You can create any conditional mean model that excludes exogenous predictors by clicking SARIMA, or you can create any conditional mean model that includes at least one exogenous predictor by clicking SARIMAX.

For multivariate model estimation, the model you choose depends on whether the selected time series are stationary or cointegrated. For stationary series, create a VAR model by clicking VAR. To include exogenous predictors, click VARX instead. For cointegrated series, click VEC.

After you select a model, the app displays the Type Model Parameters dialog box, where Type is the model type. For example, this figure shows the SARIMAX Model Parameters dialog box.

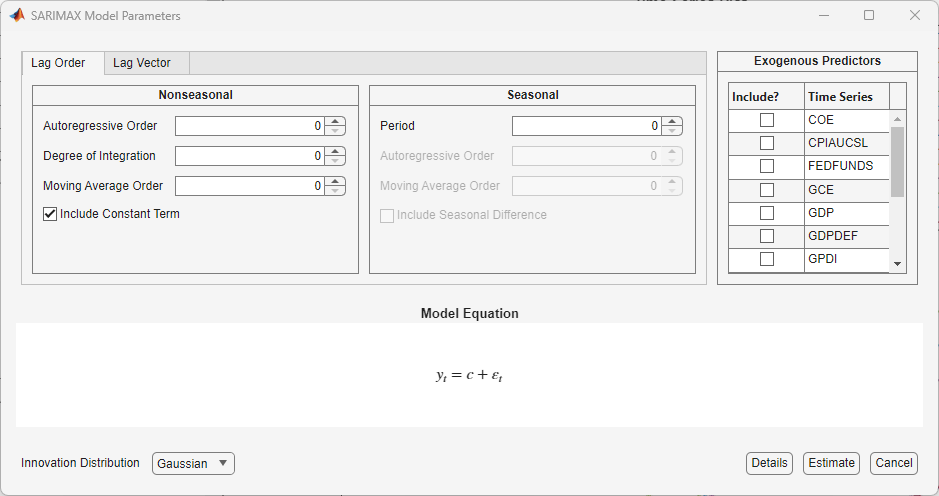
Adjustable parameters in the Type Model Parameters window depend on Type. In general, adjustable parameters include:

• Deterministic terms and linear regression coefficients corresponding to predictor variables (see Adjusting Deterministic Terms and Regression Component Parameters)

• Time series component parameters for univariate models, which include seasonal and nonseasonal lags and degrees of integration (see Adjusting Time Series Component Parameters for Univariate Models)

• Time series component parameters for multivariate models, which include AR lags and AR coefficient elements to specify equality constraints during estimation (see Adjusting Time Series Component Parameters for Multivariate Models)

• For univariate models, the innovation distribution (see Adjusting Innovation Distribution Parameters for Univariate Models)

As you adjust parameter values, the equation in the Model Equation section changes to match your specifications. Adjustable parameters correspond to input and name-value pair arguments described in corresponding model creation reference pages. For details, see the function reference page for a specific model. Regardless of the model you choose, all unspecified coefficients in the model are unknown and estimable, including the t-distribution degrees of freedom parameter (when you specify a t innovation distribution).

Note

Econometric Modeler does not support:

• Optimization option adjustments for estimation.

• Composite conditional mean and variance models. For details, see Specify Conditional Mean and Variance Models.

• Equality constraints on univariate model parameters during estimation (except for holding some parameters fixed at zero during estimation).

To adjust optimization options, estimate composite conditional mean and variance models, or apply equality constraints, use the MATLAB command line.

Adjusting Deterministic Terms and Regression Component Parameters

Supported deterministic terms depend on the selected model and include a model constant (offset or intercept) and linear time trend. To include a model constant (offset or intercept) term, select the Include Constant Term or Include Offset Term check box. Similar for a linear time trend, select the Include Trend check box. To remove a deterministic term (that is, constrain it to zero during estimation), clear the check box. The location and type of the check box in the Type Model Parameters dialog box depends on the model type. By default, Econometric Modeler includes a model constant in all model types except conditional variance models.

To select predictors for the regression component, in the Predictors list, select the check box in the Include? column corresponding to the predictors you want to include in the model. By default, the app does not include a regression component in any model type.

• If you select ARIMAX, SARIMAX, or RegARMA, then you must choose at least one predictor.

• If you select MLR, then you can specify one of the following:

  • An MLR model when you choose at least one predictor

  • A constant mean model (intercept-only model) when you clear all check boxes in the Include? column and select the Include Intercept check box

  • An error-only model when you clear all check boxes in the Include? column and clear the Include Intercept check box

Consider a linear regression model of GDP onto CPI and the unemployment rate. To specify the regression:

1. Import the DataTimeTable variable in the Data_USEconModel data set into the Econometric Modeler (see Import Time Series Variables).

2. In the Time Series pane, select the response variable GDP.

3. On the Econometric Modeler tab, in the Models section, click the arrow to display the models gallery.

4. In the models gallery, in the Regression Models section, click MLR.

5. In the MLR Model Parameters dialog box, in the Include? column, select the CPIAUCSL and UNRATE check boxes.

   

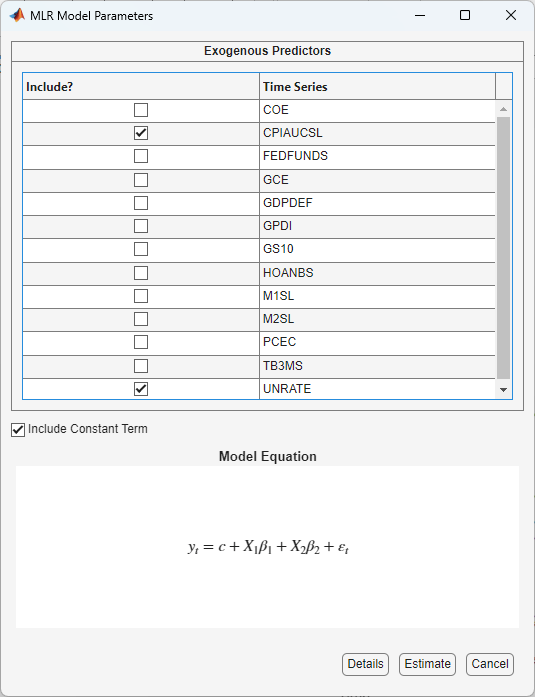
6. Click the Estimate button.

Adjusting Time Series Component Parameters for Univariate Models

In general for univariate models, time series component parameters contain lags to include in the seasonal and nonseasonal lag operator polynomials, and seasonal and nonseasonal degrees of integration.

• For conditional mean models, you can specify seasonal and nonseasonal autoregressive lags, and seasonal and nonseasonal moving average lags. You can also adjust seasonal and nonseasonal degrees of integration.

• For conditional variance models, you can specify ARCH and GARCH lags. EGARCH and GJR models also support leverage lags.

• For regression models with ARMA errors, you can specify nonseasonal autoregressive and moving average lags. For models containing seasonal lags or degrees of seasonal or nonseasonal integration, use the command line instead.

Econometric Modeler supports two options to adjust the parameters. The adjustment options are on separate tabs of the Type Model Parameters dialog box: the Lag Order and Lag Vector tabs. On the Lag Order tab, you can specify the orders of lag operator polynomials. This feature enables you to include all lags efficiently, from 1 through the specified order, in a lag operator polynomial. On the Lag Vector tab, you can specify the individual lags that comprise a lag operator polynomial. This feature is well suited for creating flexible models. For more details, see Specifying Univariate Lag Operator Polynomials Interactively.

Adjusting Innovation Distribution Parameters for Univariate Models

For univariate models, you can specify that the distribution of the innovations is Gaussian. For all models, except multiple linear regression models, you can specify the Student's t instead to address leptokurtic innovation distributions (for more details, see Maximum Likelihood Estimation for Conditional Mean Models, Maximum Likelihood Estimation for Conditional Variance Models, or Maximum Likelihood Estimation of regARIMA Models). If you specify the t distribution, then Econometric Modeler estimates its degrees of freedom parameter using maximum likelihood.

By default, Econometric Modeler uses the Gaussian distribution for the innovations. To change the innovation distribution, in the Type Model Parameters dialog box, from the Innovation Distribution button, select a distribution in the list.

Adjusting Time Series Component Parameters for Multivariate Models

Supported time series component parameters for multivariate models depend on the model type. All types enable you to include nonseasonal AR lag coefficients. However, VEC models additionally support the following parameters specifications:

• The Johansen model form, which specifies which deterministic terms (overall or within the cointegrating relation) to include in the model. For details, see Johansen Form.

• Cointegration rank r

• Adjustment speed matrix A

• Cointegration matrix B

This figure is an example of the Type Model Parameters dialog box.

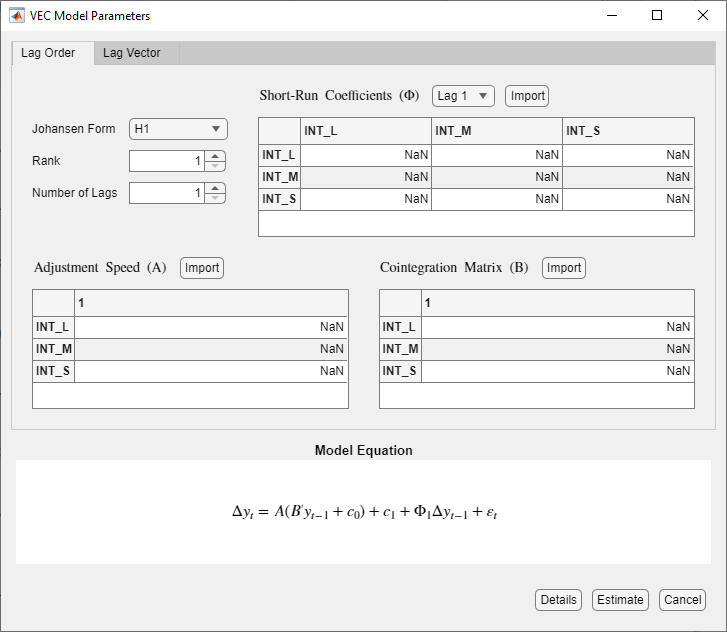
Like univariate models, Econometric Modeler supports adjusting the AR or short-run lag operator polynomial efficiently by specifying the lag order (Lag Order tab) or, for flexibility, by specifying individual lags (Lag Vector tab). Unlike univariate models, Econometric Modeler supports estimation equality constraints on individual entries of the AR or short-run lag coefficient matrix, which correspond to self- or cross-variable lag coefficients in the model. Coefficient constraints enable you to test economic scenarios. Econometric Modeler holds the specified values fixed during estimation.

For VEC models, you can specify equality constraints on the entire matrix A or B, except for Johansen forms H* and H1* which support equality constraints only for A.

To specify such equality constraints:

1. In the Type Model Parameters dialog box, select the lag to constrain by using the AR Coefficients (ϕ) (VAR or VARX) or Short-Run Coefficients (Φ) (for VEC) list.

2. Perform either one of the following alternatives:

   • Click the elements of the matrices to constrain, and then enter the value. Econometric Modeler estimates all NaN entries.

   • Import a matrix.

     1. At the command line, create an appropriately sized matrix of constraints or mix of constraints and NaN values for AR or short-run lags.

     2. In Econometric Modeler, in the Type Model Parameters dialog box, click Import.

     3. In the dialog box, select the variable to import for the coefficient matrix.

For details, see Specifying Multivariate Lag Operator Polynomials and Coefficient Constraints Interactively.

Estimating a Univariate Model

Econometric Modeler treats all parameters in the model as unknown and estimable. After you specify a model, fit it to the data by clicking Estimate in the Type Model Parameters dialog box.

Note

• Econometric Modeler requires initial values for estimable parameters and presample observations to initialize the model for estimation. Econometric Modeler always chooses the default initial and presample values as described in the estimate reference page of the model you want to estimate.

• If Econometric Modeler issues an error during estimation, then:

  • The specified model poorly describes the data. Adjust model parameters, then estimate the new model.

  • At the command line, adjust optimization options and estimate the model. For details, see Optimization Settings for Conditional Mean Model Estimation, Optimization Settings for Conditional Variance Model Estimation, or Optimization Settings for regARIMA Model Estimation.

After you estimate a model:

• A new variable that describes the estimated model appears in the Models pane with the name Type_response. Type is the model type and response is the response variable to which Econometric Modeler fit the model, for example, ARIMA_FEDFUNDS.

  You operate on an estimated model in the Models pane by right-clicking it. In addition to the options available for time series variables (see Import Time Series Variables), the context menu includes the Modify option, which enables you to modify and re-estimate a model. For example, right-click a model and select Modify. Then, in the Type Model Parameters dialog box, adjust parameters and click Estimate.

• The object display of the model appears in the Preview pane.

• The Model Summary(Type_response) document summarizing the estimation results appears in the right pane. Results shown depend on the model type. For conditional mean and regression models, results include:

  • Model Fit — A time series plot of the response series and the fitted values $$\widehat{y}$$

  • Parameters — An estimation summary table containing parameter estimates, standard errors, and t statistics and p-values for testing the null hypothesis that the corresponding parameter is 0

  • Residual Plot — A time series plot of the residuals

  • Goodness of Fit — Akaike information criterion (AIC) and Bayesian information criterion (BIC) model fit statistics

  For conditional variance models, the results also include an estimation summary table and goodness-of-fit statistics, but Econometric Modeler plots:

  • Conditional Variances — A time series plot of the inferred conditional variances $${\widehat{\sigma }}_t^2$$

  • Standardized Residuals — A time series plot of the standardized residuals $$\frac{y_t-c}{{\widehat{\sigma }}_t^2}$$, where c is the estimated offset

  You can interact with individual plots by pausing on one and selecting an interaction (see Visualizing Time Series Data). You can also interact with the summary by right-clicking the document. Options include:

  • Export — Place plot in a separate figure window.

  • Show Model — Display the summary of another estimated model by pointing to Show Model, then selecting a model in the list.

  • Show Recessions — Plot recession bands in time series plots.

Consider a SARIMA(0,1,1)×(0,1,1)₁₂ for the monthly international airline passenger numbers from 1949 to 1960 in the Data_Airline data set. To estimate this model using the Econometric Modeler:

1. Import the DataTimeTable variable in the Data_Airline data set into Econometric Modeler (see Import Time Series Variables).

2. On the Econometric Modeler tab, in the Models section, click the arrow > SARIMA.

3. In the SARIMA Model Parameters dialog box, on the Lag Order tab:

   • Nonseasonal section

     1. Set Degrees of Integration to 1.

     2. Set Moving Average Order to 1.

     3. Clear the Include Constant Term check box.

   • Seasonal section

     1. Set Period to 12 to indicate monthly data.

     2. Set Moving Average Order to 1.

     3. Select the Include Seasonal Difference check box.

   

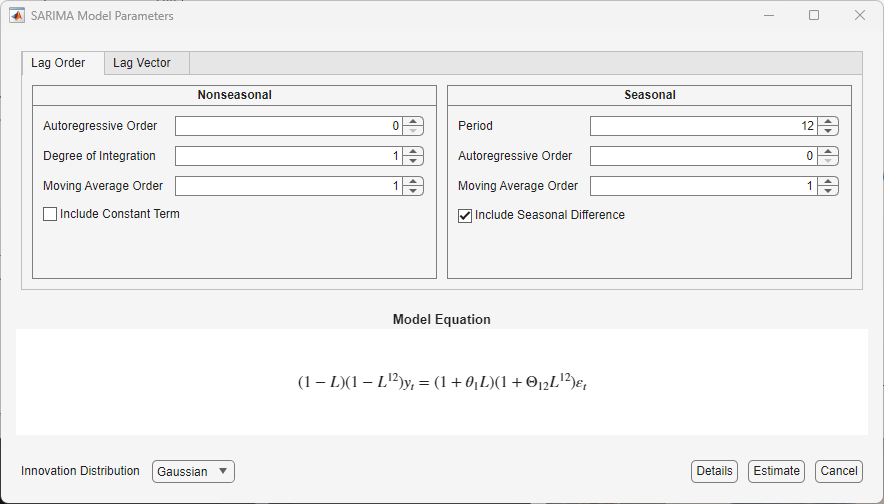
4. Click Estimate.

As a result:

• A variable named SARIMA_PSSG appears in the Models pane.

• The value of SARIMA_PSSG appears in the Preview pane.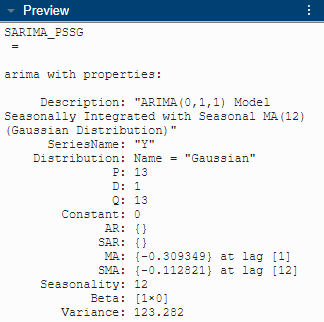

  

• An estimation summary appears in the new Model Summary(SARIMA_PSSG) document.

  

Estimating a Multivariate Model

Econometric Modeler treats all parameters in the model as unknown and estimable by default. However, unlike univariate models, Econometric Modeler supports equality constraints on some parameters for estimation. You can specify coefficient values in the app or import a lag coefficient matrix from the workspace.

After you configure the model, fit it to the data by clicking Estimate in the Type Model Parameters dialog box.

Note

• To initialize the model for estimation, Econometric Modeler removes the first p observations from the response data to use as a presample, and then the function fits the model to the remaining observations.

• If Econometric Modeler issues an error during estimation, the specified model poorly describes the data. Adjust model parameters, and then estimate the new model.

After you estimate a model, Econometric Modeler shows results similar to that of univariate estimation (see Estimating a Univariate Model), and you can interact with an estimated multivariate model in the same ways as with univariate models. Notable differences include:

• A new variable that describes the estimated model appears in the Models pane with the name Typej, where Type is the model type and j is estimated model j of that type, for example, VAR2 is the second estimated VAR model during the session.

• The Model Summary(Type_response) document summarizing the estimation results appears in the right pane. However, the plots shown depend on the model type and the selected time series in the Time Series list at the top of the document. For VAR models, results include:

  • Model Fit — A time series plot of the selected time series and the corresponding fitted values $$\widehat{y}$$

  • Residual Plot — A time series plot of the residuals corresponding to the selected time series

  For VEC models, the results additionally include a time series plot of the cointegrating relation, which is invariant to the selected time series.

Consider a 3-D VAR(4) model of quarterly measurements of the US gross domestic product (GDP), M1 money supply, and the 3-month T-bill rate from 1947 through 2009. The file Data_USEconModel.mat contains the series, among other economic measurements.

To estimate this model using the Econometric Modeler:

1. Import the DataTimeTable variable in the Data_USEconModel data set into Econometric Modeler (see Import Time Series Variables).

2. On the Econometric Modeler tab, in the Time Series pane, click GDP, and then press Ctrl and click M1SL.

3. Because GDP and M1SL exhibit exponential growth, use their growth rates in the model. On the Econometric Modeler tab, in the Transforms section, click Log, and then click Difference. Change the name of the transformed variables to GDPRate and M1SLRate, respectively.

4. In the Time Series pane, click TB3MS, and then stabilize the series by clicking, in the Transforms section, Difference. Change the name of the transformed series to TB3MSRate.

5. With TB3MSRate selected, select the three rate series for the VAR model by pressing Ctrl and clicking GDPRate and M1SLRate.

6. On the Econometric Modeler tab, in the Models section, click VAR.

7. In the VAR Model Parameters dialog box, on the Lag Order tab, set Autoregressive Order to 4.

   

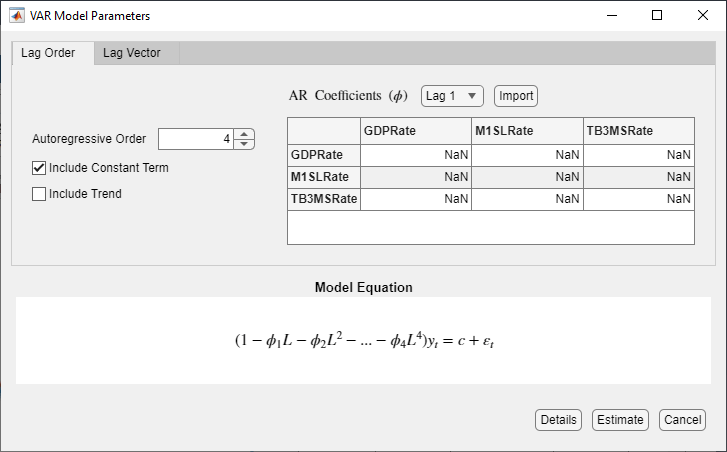
8. Click Estimate.

As a result:

• A variable named VAR appears in the Models pane.

• The value of VAR appears in the Preview pane.

  

• An estimation summary appears in the new Model Summary(VAR) document. The plots are relative to the GDPRate series. The indices of the parameter estimates in the Parameters section correspond to the order of the series in the Time Series list (for example AR{1}(2,3) is the lag 1 AR coefficient of the TB3MSRate series in the equation of the M1SLRate series.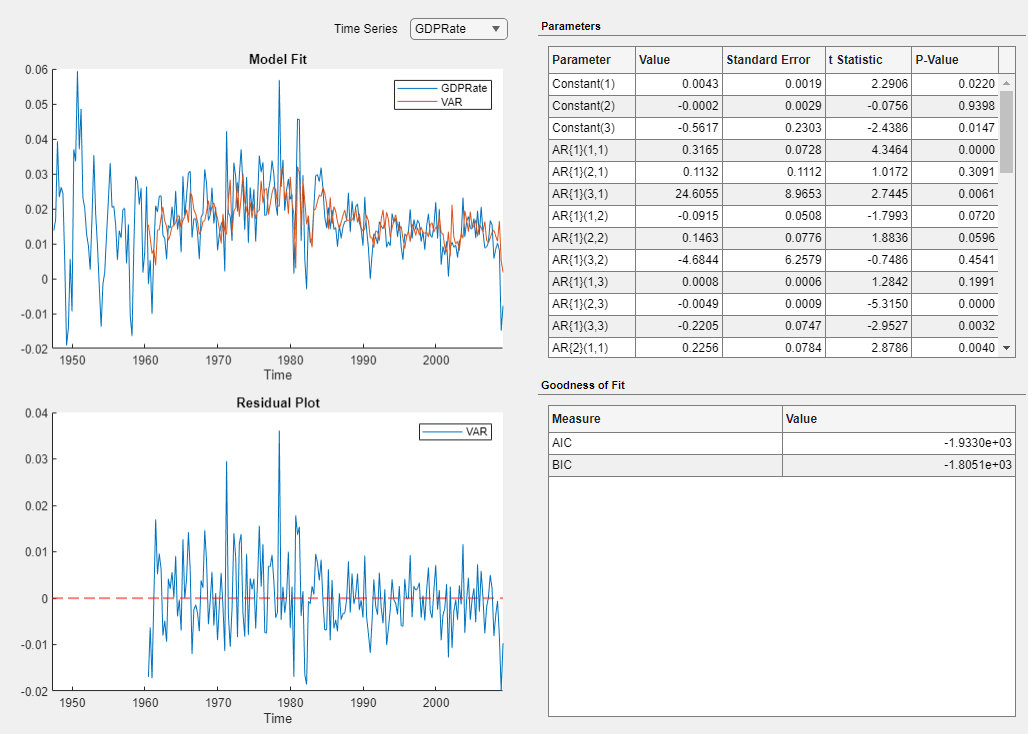

  

Conducting Goodness-of-Fit Checks

After you estimate a model, a good practice is to determine the adequacy of the fitted model (see Goodness of Fit). Econometric Modeler is well suited for visually assessing the in-sample fit (for all models except conditional variance models) and performing residual diagnostics.

Residual diagnostics include evaluating the model assumptions and investigating whether you must respecify the model to address other properties of the data. Model assumptions to assess include checking whether the residuals are centered on zero, normally distributed, homoscedastic, and serially uncorrelated. If the residuals do not demonstrate all these properties, then you must determine the severity of the departure, whether to transform the data, and whether to specify a different model. For more details on residual diagnostics, see Time Series Regression VI: Residual Diagnostics and Residual Diagnostics.

To perform goodness-of-fit checks using Econometric Modeler, in the Models pane, select an estimated model. Then, complete the following steps:

• To visually assess the in-sample fit for all models (except conditional variance models), inspect the Model Fit plot in the Model Summary document. For multivariate models, Econometric Modeler displays fitted values of one series. You can select a different series in the model to plot by clicking the series in the Time Series list.

• To visually assess whether the residuals are centered on zero, autocorrelated, and heteroscedastic, inspect the Residual Plot in the Model Summary document. For multivariate models, Econometric Modeler displays residuals of one series. You can select a different residual series to plot by clicking the corresponding series in the Time Series list.

• On the Econometric Modeler tab, in the Diagnostics section, click Residual Diagnostics. The diagnostics gallery provides these residual plots and tests.

  Method	Diagnostic
  Residual histogram	Visually assess normality
  Residual quantile-quantile plot	Visually assess normality and skewness
  ACF	Visually assess whether residuals are autocorrelated
  Ljung-Box Q-test	Test residuals for significant autocorrelation
  ACF of squared residuals	Visually assess whether residuals have conditional heteroscedasticity
  Engle's ARCH test	Test residuals for conditional heteroscedasticity (significant ARCH effects)

  Alternatively, to plot a histogram, quantile-quantile plot, or ACF of the residuals of an estimated model:

  1. Select a model in the Models pane.

  2. Click the Plots tab.

  3. In the Plots section, click the arrow and then click one of the plots in the Model Plots section of the gallery.

  For multivariate models:

  • Econometric Modeler plots residual diagnostics for all model series within the same document.

  • Econometric Modeler runs residual diagnostic tests simultaneously for all series, but it shows results of each residual series separately. You can choose which results to show by clicking, in the test tab, the series in the Time Series list.

Note

Another important goodness-of-fit check is predictive-performance assessment. To assess the predictive performance of several models:

1. Fit a set of models to the data using Econometric Modeler.

2. Perform residual diagnostics on all models.

3. Choose a subset of models with desirable residual properties and minimal fit statistics (see Finding Model with Best In-Sample Fit).

4. Export the chosen models to the MATLAB Workspace (see Export Session Results).

5. Perform a predictive performance assessment at the command line (see Assess Predictive Performance).

For an example, see Compare Predictive Performance After Creating Models Using Econometric Modeler.

Consider performing goodness-of-fit checks on the estimated SARIMA(0,1,1)×(0,1,1)₁₂ model for the airline counts data in Estimating a Univariate Model.

1. In the right pane, on the Model Summary(SARIMA_PSSG) document:

   1. Model Fit suggests that the model fits to the data fairly well.

      

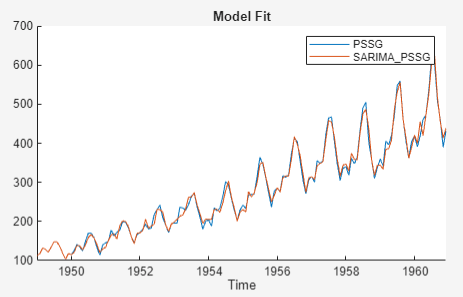
   2. Residual Plot suggests that the residuals have a mean of zero. However, the residuals appear heteroscedastic and serially correlated.

      

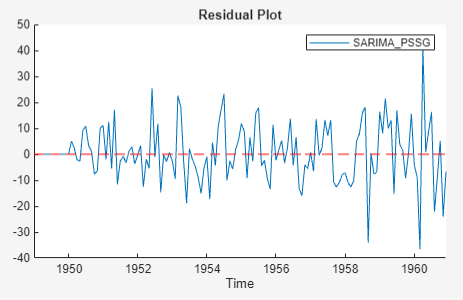
2. On the Econometric Modeler tab, in the Diagnostics section, click Residual Diagnostics. In the diagnostics gallery:

   1. Click Residual Q-Q Plot. The right pane display a figure window named QQPlot(SARIMA_PSSG) containing a quantile-quantile plot of the residuals.

      

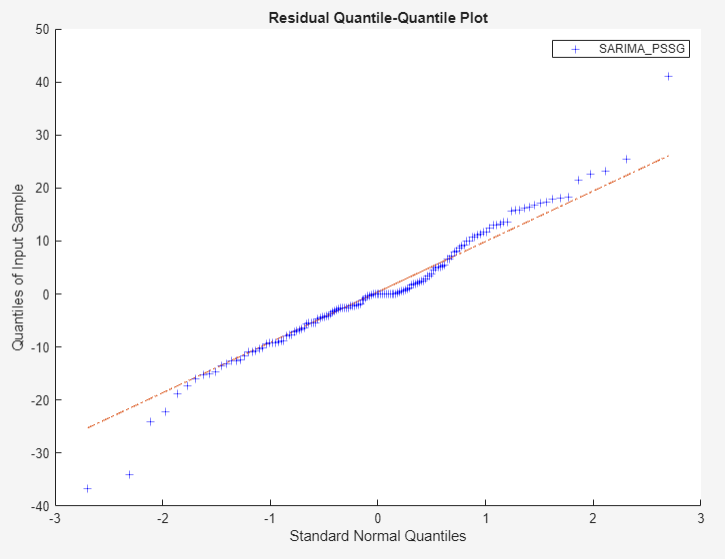
      The plot suggests that the residuals are approximately normal, but with slightly heavier tails.

   2. Click Autocorrelation Function. In the toolstrip, the ACF tab appears and contains plot options. The right pane displays a figure window named ACF(SARIMA_PSSG) containing the ACF of the residuals.

      

      Because almost all the sample autocorrelation values are below the confidence bounds, the residuals are likely not serially correlated.

   3. Click Engle's ARCH Test. On the ARCH tab, in the Tests section, click Run Test to run the test using default options. The right pane displays the ARCH(SARIMA_PSSG) document, which shows the test results in the Results table.

      

      The results suggest rejection of the null hypothesis that the residuals exhibit no ARCH effects at a 5% level of significance. You can try removing heteroscedasticity by applying the log transformation to the series.

Finding Model with Best In-Sample Fit

Econometric Modeler enables you to fit multiple related models to a data set efficiently. After you estimate a model, you can estimate other models by iterating the methods in Perform Exploratory Data Analysis, Fitting Models to Data, and Conducting Goodness-of-Fit Checks. After each iteration, a new model variable appears in the Models pane.

For models in the same parametric family that you fit to the same response series, you can determine the model with the best parsimonious, in-sample fit among the estimated models by comparing their fit statistics. From a subset of candidate models, to determine the model of best fit using Econometric Modeler:

1. In the Models pane, double-click an estimated model. In the right pane, estimation results of the model appear in the Model Summary(Model) document, where Model is the name of the selected model.

2. On the Model Summary(Model) document, in the Goodness of Fit table, choose a fit statistic (AIC or BIC) and record its value.

3. Iterate the previous steps for all candidate models.

4. Choose the model that yields the minimal fit statistic.

For more details on goodness-of-fit statistics, see Information Criteria for Model Selection.

Consider finding the best-fitting SARIMA model, with a period of 12, for the log of the airline passenger counts in the Data_Airline data set. Fit a subset of SARIMA models, considering all combinations of models that include up to two seasonal and nonseasonal MA lags.

1. Import the DataTimeTable variable in the Data_Airline data set into Econometric Modeler (see Import Time Series Variables).

2. Apply the log transformation to PSSG (see Transforming Time Series).

3. Fit a SARIMA(0,1,q)×(0,1,q₁₂)₁₂ to PSSGLog, where all unknown orders are 0 (see Estimating a Univariate Model).

4. In the right pane, on the Model Summary(SARIMA_PSSGLog) document, in the Goodness of Fit table, record the AIC value.

   

5. In the Models pane, select PSSGLog.

6. Iterate steps 4 and 5, but adjust q and q₁₂ to cover the nine permutations of q ∈ {0,1,2} and q₁₂ ∈ {0,1,2}. Econometric Modeler distinguishes subsequent models of the same type by appending consecutive digits to the end of the variable name.

The resulting AIC values are in this table.

Model	Variable Name	AIC
SARIMA(0,1,0)×(0,1,0)12	SARIMA_PSSGLog1	-491.8042
SARIMA(0,1,0)×(0,1,1)12	SARIMA_PSSGLog2	-530.5327
SARIMA(0,1,0)×(0,1,2)12	SARIMA_PSSGLog3	-528.5330
SARIMA(0,1,1)×(0,1,0)12	SARIMA_PSSGLog4	-508.6853
SARIMA(0,1,1)×(0,1,1)12	SARIMA_PSSGLog5	-546.3970
SARIMA(0,1,1)×(0,1,2)12	SARIMA_PSSGLog6	-544.6444
SARIMA(0,1,2)×(0,1,0)12	SARIMA_PSSGLog7	-506.8027
SARIMA(0,1,2)×(0,1,1)12	SARIMA_PSSGLog8	-544.4789
SARIMA(0,1,2)×(0,1,2)12	SARIMA_PSSGLog9	-542.7171

Because it yields the minimal AIC, the SARIMA(0,1,1)×(0,1,1)₁₂ model is the model with the best parsimonious, in-sample fit.

Export Session Results

Econometric Modeler offers several options for you to share your session results. The option you choose depends on your analysis goals.

The options for sharing your results are in the Export section of the Econometric Modeler tab. This table describes the available options.

Option	Description
Export Variables	Export time series and model variables to the MATLAB Workspace. Choose this option to perform further analysis at the MATLAB command line. For example, you can generate forecasts from an estimated model or check the predictive performance of several models.
Generate Function	Generate a MATLAB function to use outside the app. The function accepts the data loaded into the app as input, and outputs a model estimated in the app session. Choose this option to: Understand the functions used by Econometric Modeler to create and estimate the model. Modify the generated function in the MATLAB Editor for further use.
Generate Live Function	Generate a MATLAB live function to use outside the app. The function accepts the data loaded into the app as input, and outputs a model estimated in the app session. Choose this option to: Understand the functions used by Econometric Modeler to create and estimate the model. Modify the generated function in the Live Editor for further use.
Generate Report	Generate a report that summarizes the session. Choose this option when you achieve your analysis goals in Econometric Modeler, and you want to share a summary of the results.

Exporting Variables

To export time series and estimated model variables from the Time Series or Models pane to the MATLAB Workspace:

1. On the Econometric Modeler tab, in the Export section, click or Export > Export Variables.

2. In the Export Variables dialog box, all time series variables appear in the left pane and all model variables appear in the right pane. Choose time series and model variables to export by selecting the corresponding check boxes in the Select column. The app selects the check box of all time series or model variables that are selected in the Time Series and Models panes. Clear any check boxes for variables to you do not want to export. For example, this figure shows how to select the PSSGLog time series and the SARIMA_PSSGLog SARIMA model.

   

3. Click Export.

The selected variables appear in the MATLAB Workspace. Time series variables are double-precision column vectors. Estimated models are objects of type depending on the model (for example, an exported ARIMA model is an arima object).

Alternatively, you can export variables by selecting at least one variable, right-clicking a selected variable, and selecting Export.

Generating a Function

The app can generate a plain text function or a live function. The main difference between the two functions is the editor used to modify the generated function: you edit plain text functions in the MATLAB editor and live functions in the Live Editor. For more details on the differences between the two function types, see What Is a Live Script or Function?.

Regardless of the function type you choose, the generated function accepts the data loaded into the app as input, and outputs a model estimated in the app session. To export a MATLAB function or live function that creates a model estimated in an app session:

1. In the Models pane, select an estimated model.

2. On the Econometric Modeler tab, in the Export section, click Export. In the Export menu, choose Generate Function or Generate Live Function.

The MATLAB Editor or Live Editor displays an untitled, unsaved function containing the code that estimates the model.

• By default, the function name is modelTimeSeries.

• The function accepts the originally imported data set as input.

• Before the function estimates the model, it extracts the variables from the input data set used in estimation, and applies the same transformations to the variables that you applied in Econometric Modeler.

• The function returns the selected estimated model.

Consider generating a live function that returns SARIMA_PSSGLog, the SARIMA(0,1,1)×(0,1,1)₁₂ model fit to the log of airline passenger data (see Estimating a Univariate Model). This figure shows the generated live function.

Generating a Report

Econometric Modeler can produce a report describing your activities on selected time series and model variables. The app organizes the report into chapters corresponding to selected time series and model variables. Chapters describe session activities that you perform on the corresponding variable.

Chapters on time series variables describe transformations, plots, and tests that you perform on the selected variable in the session. Estimated model chapters contain an estimation summary, that is, elements of the Model Summary document (see Estimating a Univariate Model), and residual diagnostics plots and tests.

You can export the report as one of the following document types:

• Hypertext Markup Language (HTML)

• Microsoft^® Word XML Format Document (DOCX)

• Portable Document Format (PDF)

To export a report:

1. On the Econometric Modeler tab, in the Export section, click Export > Generate Report.

2. In the Select Variables for Report dialog box, all time series variables in the Time Series pane appear in the left pane and all model variables in the Models pane appear in the right pane. Choose variables to include the report by selecting their check boxes in the Select column.

3. Select a document type by clicking Report Format and selecting the format you want.

4. Click OK.

5. In the Select File to Write window:

   1. Browse to the folder in which you want to save the report.

   2. In the File name box, type a name for the report.

   3. Click Save.

Consider generating an HTML report for the analysis of the airline passenger data (see Conducting Goodness-of-Fit Checks). This figure shows how to select all variables and the HTML format.

This figure shows a sample of the generated report.

References

[1] Box, George E. P., Gwilym M. Jenkins, and Gregory C. Reinsel. Time Series Analysis: Forecasting and Control. 3rd ed. Englewood Cliffs, NJ: Prentice Hall, 1994.