Compare Conditional Variance Model Fit Statistics Using Econometric Modeler App
This example shows how to specify and fit GARCH, EGARCH, and GJR
models to data using the Econometric Modeler app. Then, the example determines the
model that fits to the data the best by comparing fit statistics. The data set,
which is stored in Data_FXRates.mat, contains foreign exchange
rates measured daily from 1979–1998.
Consider creating a predictive model for the Swiss franc to US dollar exchange
rate (CHF).
Import Data into Econometric Modeler
At the command line, load the Data_FXRates.mat data
set.
load Data_FXRatesAt the command line, open the Econometric Modeler app.
econometricModeler
Alternatively, open the app from the apps gallery (see Econometric Modeler).
Import DataTimeTable into the app:
On the Econometric Modeler tab, in the Import section, click the Import button
 .
.In the Import Data dialog box, in the Import? column, select the check box for the
DataTimeTablevariable.Click Import.
All time series variables in DataTimeTable appear in the
Time Series pane, and a time series plot of all the
series appears in the Time Series Plot(AUD) figure
window.
Plot the Series
Plot the Swiss franc exchange rates by double-clicking the
CHF time series in the Time
Series pane.
Highlight periods of recession:
In the Time Series Plot(CHF) figure window, right-click the plot.
In the context menu, select Show Recessions.

The CHF series appears to have a stochastic
trend.
Stabilize the Series
Stabilize the Swiss franc exchange rates by applying the first difference to
CHF.
In the Time Series pane, select
CHF.On the Econometric Modeler tab, in the Transforms section, click Difference.
Highlight periods of recession:
In the Time Series Plot(CHFDiff) figure window, right-click the plot.
In the context menu, select Show Recessions.
A variable named
CHFDiff, representing the differenced series, appears in the Time Series pane, its value appears in the Preview pane, and its time series plot appears in the Time Series Plot(CHFDiff) figure window.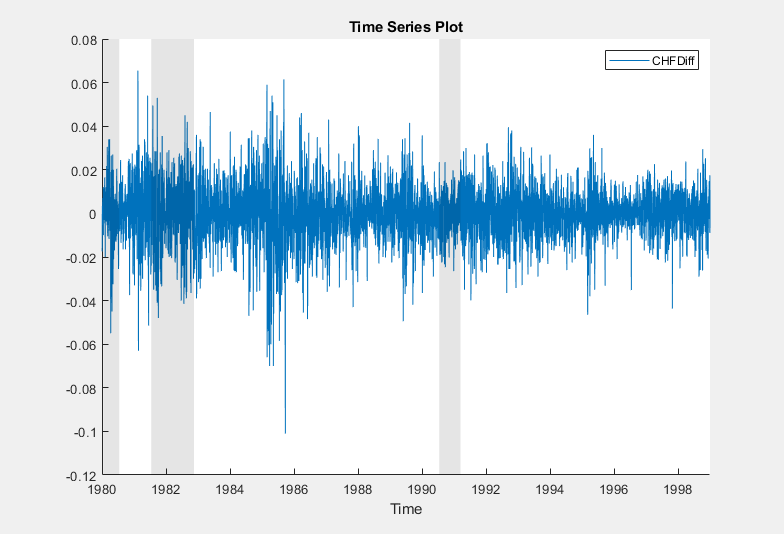
The series appears to be stable, but it exhibits volatility clustering.
Assess Presence of Conditional Heteroscedasticity
Test the stable Swiss franc exchange rate series for conditional heteroscedasticity by conducting Engle's ARCH test. Run the test assuming an ARCH(1) alternative model, then run the test again assuming an ARCH(2) alternative model. Maintain an overall significance level of 0.05 by decreasing the significance level of each test to 0.05/2 = 0.025.
In the Time Series pane, select
CHFDiff.On the Econometric Modeler tab, in the Tests section, click New Test > Engle's ARCH Test.
On the ARCH tab, in the Parameters section, set Number of Lags of
1.Set Significance Level to
0.025.In the Tests section, click Run Test.
Repeat steps 3 through 5, but set Number of Lags to
2instead.
The test results appear in the Results table of the ARCH(CHFDiff) document.

The tests reject the null hypothesis of no ARCH effects against the
alternative models. This result suggests specifying a conditional variance model
for CHFDiff containing at least two ARCH lags.
Conditional variance models with two ARCH lags are locally equivalent to models
with one ARCH and one GARCH lag. Consider GARCH(1,1), EGARCH(1,1), and GJR(1,1)
models for CHFDiff.
Estimate GARCH Model
Specify a GARCH(1,1) model and fit it to the
CHFDiff series.
In the Time Series pane, select the
CHFDifftime series.Click the Econometric Modeler tab. Then, in the Models section, click the arrow to display the models gallery.
In the models gallery, in the GARCH Models section, click GARCH.
In the GARCH Model Parameters dialog box, on the Lag Order tab:
Set GARCH Degree to
1.Set ARCH Degree to
1.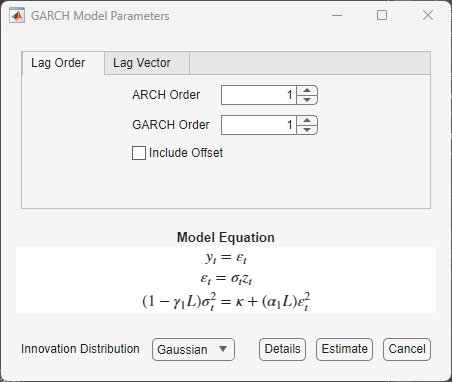
Click Estimate.
The model variable GARCH_CHFDiff appears in the Models pane, its value appears in the Preview pane, and its estimation summary appears in the Model Summary(GARCH_CHFDiff) document.

Specify and Estimate EGARCH Model
Specify an EGARCH(1,1) model containing a leverage term at the first lag, and
fit the model to the CHFDiff series.
In the Time Series pane, select the
CHFDifftime series.On the Econometric Modeler tab, in the Models section, click the arrow to display the models gallery.
In the models gallery, in the GARCH Models section, click EGARCH.
In the EGARCH Model Parameters dialog box, on the Lag Order tab:
Set GARCH Degree to
1.Set ARCH Degree to
1. Consequently, the app includes a corresponding leverage lag. You can remove or adjust leverage lags on the Lag Vector tab.
Click Estimate.
The model variable EGARCH_CHFDiff appears in the Models pane, its value appears in the Preview pane, and its estimation summary appears in the Model Summary(EGARCH_CHFDiff) document.
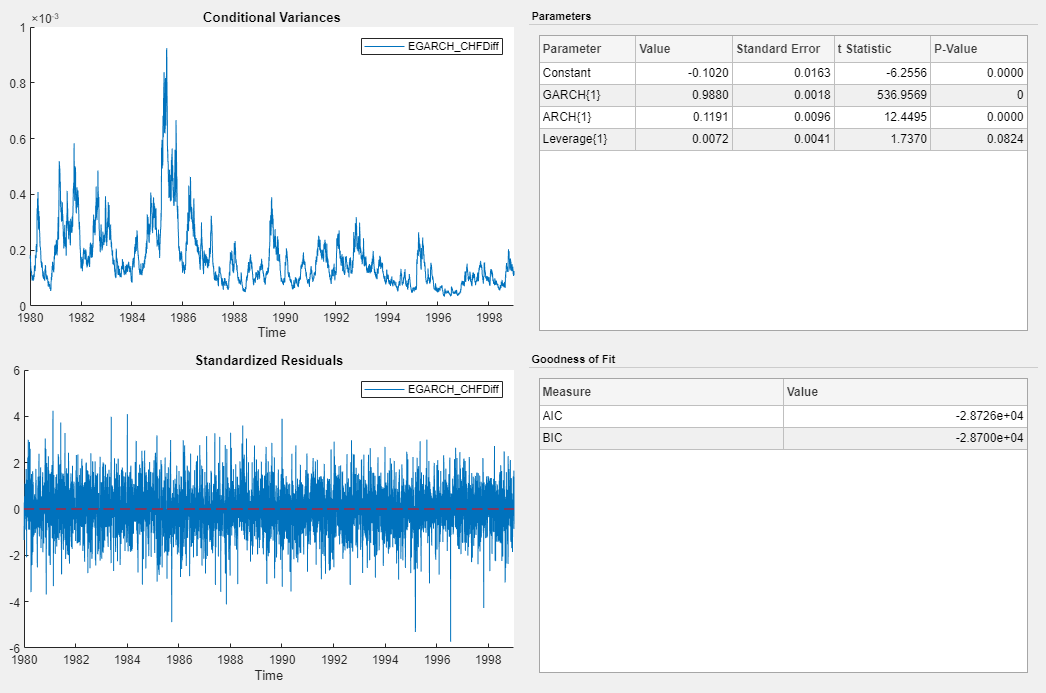
Specify and Estimate GJR Model
Specify a GJR(1,1) model containing a leverage term at the first lag, and fit
the model to the CHFDiff series.
In the Time Series pane, select the
CHFDifftime series.On the Econometric Modeler tab, in the Models section, click the arrow to display the models gallery.
In the models gallery, in the GARCH Models section, click GJR.
In the GJR Model Parameters dialog box, on the Lag Order tab:
Set GARCH Degree to
1.Set ARCH Degree to
1. Consequently, the app includes a corresponding leverage lag. You can remove or adjust leverage lags on the Lag Vector tab.Click Estimate.
The model variable GJR_CHFDiff appears in the Models pane, its value appears in the Preview pane, and its estimation summary appears in the Model Summary(GJR_CHFDiff) document.
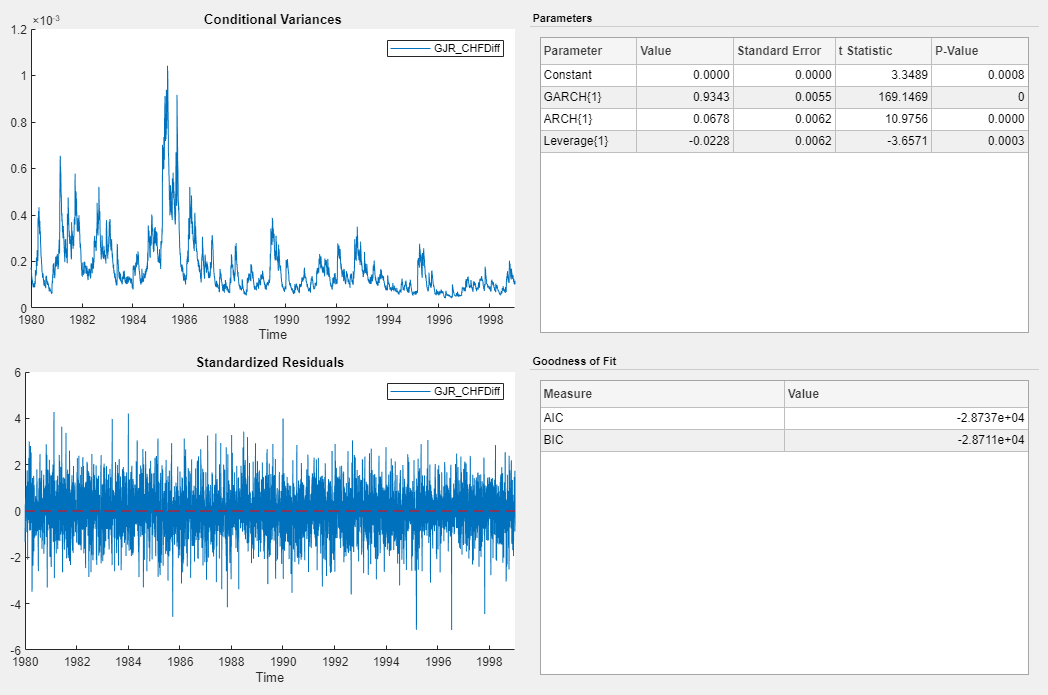
Choose Model
Choose the model with the best parsimonious in-sample fit. Base your decision on the model yielding the minimal Akaike information criterion (AIC). The table shows the AIC fit statistics of the estimated models, as given in the Goodness of Fit section of the estimation summary of each model.
| Model | AIC |
|---|---|
| GARCH(1,1) | -28730 |
| EGARCH(1,1) | -28726 |
| GJR(1,1) | -28737 |
The GJR(1,1) model yields the minimal BIC value. Therefore, it has the best parsimonious in-sample fit of all the estimated models.