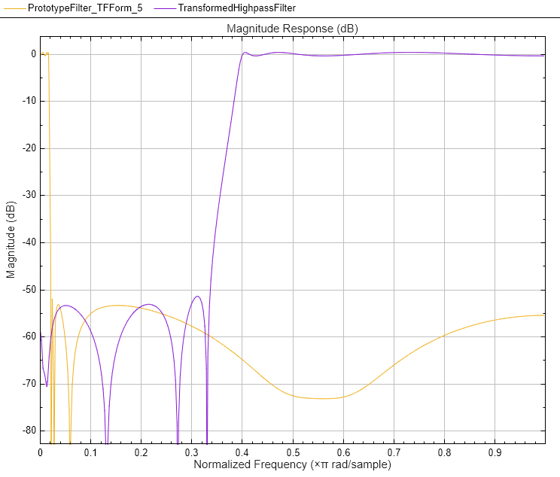
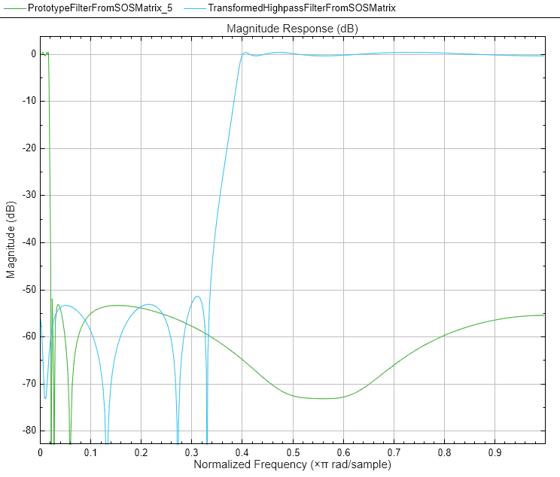
iirlp2hp
Transform lowpass IIR filter to highpass filter
Description
[
transforms a lowpass IIR filter to a highpass IIR filter.num,den] = iirlp2hp(b,a,wo,wt)
The iirlp2hp function returns the numerator and denominator
coefficients of the transformed highpass filter. The function accepts
wo, frequency value to be transformed from the prototype
filter, and wt, desired frequency in the transformed highpass
filter, and applies the lowpass to highpass frequency transformation on the input
prototype filter. The input prototype lowpass filter is specified with the numerator
and denominator coefficients, b and a
respectively. For more details on the transformation, see IIR Lowpass to Highpass Frequency Transformation.
[
additionally returns the numerator and the denominator coefficients of the mapping
filter.num,den,allpassNum,allpassDen] =
iirlp2hp(b,a,wo,wt)
Examples
Input Arguments
Output Arguments
More About
References
[1] Nowrouzian, B., and A.G. Constantinides. “Prototype Reference Transfer Function Parameters in the Discrete-Time Frequency Transformations.” In Proceedings of the 33rd Midwest Symposium on Circuits and Systems, 1078–82. Calgary, Alta., Canada: IEEE, 1991. https://doi.org/10.1109/MWSCAS.1990.140912.
[2] Nowrouzian, B., and L.T. Bruton. “Closed-Form Solutions for Discrete-Time Elliptic Transfer Functions.” In [1992] Proceedings of the 35th Midwest Symposium on Circuits and Systems, 784–87. Washington, DC, USA: IEEE, 1992. https://doi.org/10.1109/MWSCAS.1992.271206.
[3] Constantinides, A.G.“Spectral transformations for digital filters.” Proceedings of the IEEE, vol. 117, no. 8: 1585-1590. August 1970.
Extended Capabilities
Version History
Introduced in R2011a