iirlp2lp
Transform lowpass IIR filter to different lowpass filter
Description
[
transforms lowpass IIR filter to different lowpass filter.num,den] = iirlp2lp(b,a,wo,wt)
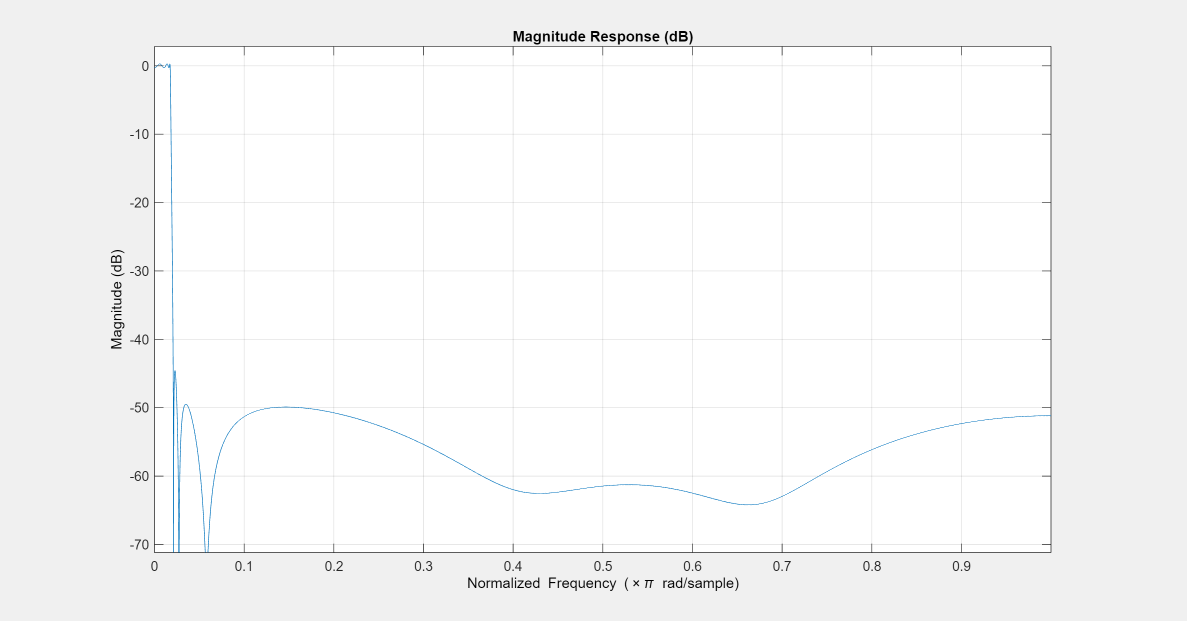
The prototype lowpass filter is specified with the numerator and denominator
coefficients, b and a respectively. The
function returns the numerator and denominator coefficients of the transformed
lowpass digital filter.
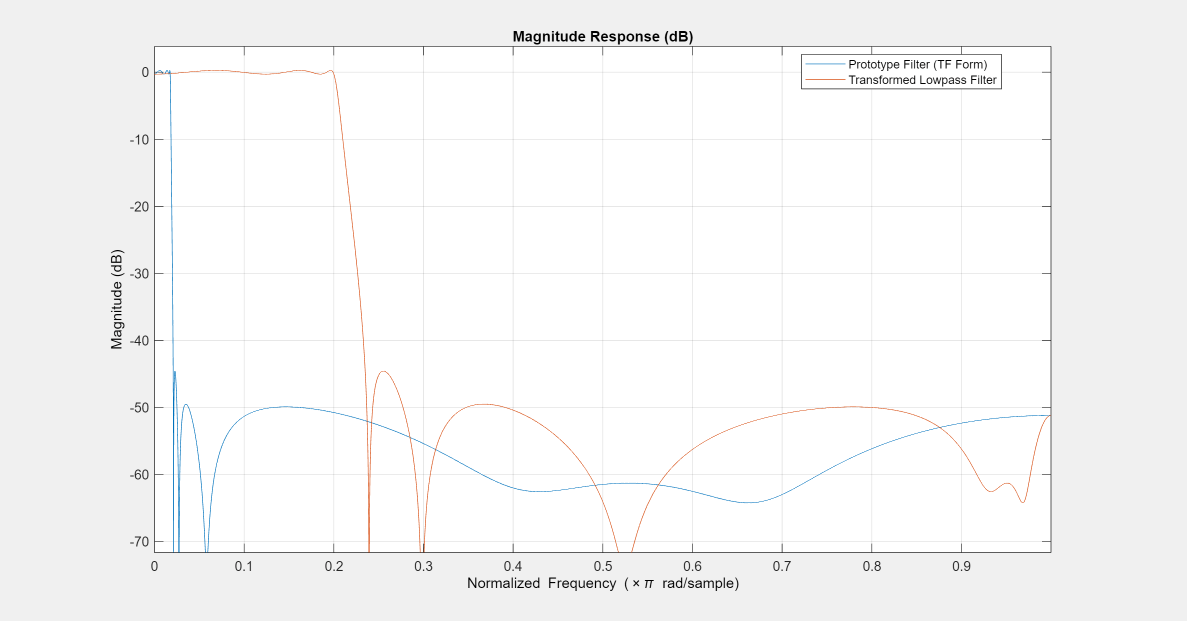
The function transforms the magnitude response from lowpass to a different lowpass. For more details, see Lowpass IIR Filter to Different Lowpass Filter Transformation.
[
in addition returns the numerator and the denominator coefficients of the allpass
mapping filter.num,den,allpassNum,allpassDen] =
iirlp2lp(b,a,wo,wt)
Examples
Input Arguments
Output Arguments
More About
References
[1] Nowrouzian, B., and A.G. Constantinides. “Prototype Reference Transfer Function Parameters in the Discrete-Time Frequency Transformations.” In Proceedings of the 33rd Midwest Symposium on Circuits and Systems, 1078–82. Calgary, Alta., Canada: IEEE, 1991. https://doi.org/10.1109/MWSCAS.1990.140912.
[2] Nowrouzian, B., and L.T. Bruton. “Closed-Form Solutions for Discrete-Time Elliptic Transfer Functions.” In [1992] Proceedings of the 35th Midwest Symposium on Circuits and Systems, 784–87. Washington, DC, USA: IEEE, 1992. https://doi.org/10.1109/MWSCAS.1992.271206.
[3] Constantinides, A.G.“Spectral transformations for digital filters.” Proceedings of the IEEE, vol. 117, no. 8: 1585-1590. August 1970.
Extended Capabilities
Version History
Introduced in R2011a