Raised Cosine Receive Filter
Apply matched filtering using raised cosine FIR filter
Libraries:
Communications Toolbox /
Comm Filters
Communications Toolbox HDL Support /
Comm Filters
Description
The Raised Cosine Receive Filter block filters the input signal using a raised cosine finite impulse response (FIR) filter and optionally decimates the filtered signal. The FIR filter has (Filter span in symbols × Input samples per symbol + 1) tap coefficients. The block icon shows the impulse response of the filter. For more information, see Algorithms.
Examples
The Raised Cosine Transmit Filter and Raised Cosine Receive Filter blocks are designed for raised cosine (RC) filtering. Each block can apply a square-root raised cosine (RRC) filter or a raised cosine filter to a signal. You can vary the roll-off factor and span of the filter.
The Raised Cosine Transmit Filter and Raised Cosine Receive Filter blocks are tailored for use at the transmitter and receiver, respectively. The transmit filter upsamples (interpolates) the output signal. The receive filter expects its input signal to be upsampled and downsamples (decimates) the output signal, based on the configured settings of the block.
The raised cosine transmit and receive filter blocks each introduce a propagation delay, as described in Group Delay.
The doc_rrcfiltercompare.slx model shows how to split the filtering equally between the transmitter and the receiver by using a pair of square root raised cosine filters. The use of a matched pair of square root raised cosine filters is equivalent to a single normal raised cosine filter. The filters share the same span and use the same number samples per symbol but the two filter blocks on the upper path have a square root shape and the single filter block on the lower path has the normal shape.

Run the model and observe the eye and constellation diagrams. The performance is nearly identical for the two methods. Note that the limited impulse response of practical square root raised cosine filters causes a slight difference between the response of two cascaded square root raised cosine filters and the response of one raised cosine filter.




Apply raised cosine matched filtering to a modulated signal by applying transmit and receive root raised cosine (RRC) filtering to the input signal. Demonstrate input signal power adjustment for correct SNR and the delay adjustment for correct error rate calculation.
The cm_tx_rx_rrc_filter model outputs frames of random integers by using a Random Integer Generator block. The frames of data pass through a QPSK Modulator Baseband block, Raised Cosine Transmit Filter, AWGN Channel block, Raised Cosine Receive Filter, and QPSK Demodulator Baseband block. Separate Error Rate Calculation blocks compute the bit error rate after QPSK demodulation, with and without accounting for the delay of the received signal due to the transmit and receive filtering.
The model initializes the variables that configure block parameters by using the PreLoadFcn callback function. For more information, see Model Callbacks (Simulink). The model demonstrates configuration of parameters to set the input signal power level for AWGN based on filter oversampling, and to set the delay for the error rate calculation path based on the filter delay.

The QPSK-modulated signal has unity power, but signal oversampling by the transmit RRC filtering reduces the signal level by the oversampling rate. To apply the correct noise level, you must adjust the input signal power in the AWGN block to account for the reduced signal level due to oversampling by the filter. A Variance block computes a variance to be approximately one over the oversampling rate, 1/8.
Computed variance = 0.1250

A Time Scope plots the Received, Delayed, and Not delayed signals. The Delayed signal aligns with the Received signal, but the Not delayed signal is shifted by 10 samples. The error rate calculation shows the correct BER when you account for the filter delay.
Delay not accounted for: BER = 0.75 Delay accounted for: BER = 0.00462
Recover frame synchronization in a QPSK system impaired by a variable timing error. The example shows the benefit of performing symbol synchronization to assist the frame synchronization.
The cm_ex_symbol_frame_sync model compares frame synchronization performance with and without symbol synchronization. The Variable Fractional Delay block introduces a varying timing error to a root raised cosine (RRC) filtered QPSK signal. After the AWGN block, the receive path is duplicated to compare performance with and without a Symbol Synchronizer block in the path. The Symbol Synchronizer block corrects for clock skew between the transmitter and receiver, aligning the output signal with a valid clock reference. For the timing error conditions in this example, the symbol synchronizer returns a vector containing 99, 100, or 101 symbols for a 200-sample input vector.
The Frame Synchronizer block aligns the symbol stream along correct frame boundaries using the frame header present in the signal. It also provides the valid frame indicator signal to the BER Data Decoding subsystem, which calculates the bit error rate (BER). To avoid calculating the BER on nonvalid frames, the BER Data Decoding subsystem regenerates the input data bits rather than using the Bit Generation block output.

For a 20 dB signal-to-noise ratio and variable timing error in the range of [0, 0.9] samples, signal recovery is successful on the receiver path that includes symbol synchronization. The timing error varies over time, causing the constellation to oscillate between corrupted and clean states as seen in the Before Sym Sync signal in the Constellation Diagram block. The After Sym Sync signal in the constellation diagram shows that the symbol synchronizer removes the variable timing error signal impairment.

The BER with and without symbol synchronization show the performance improvement due to the Symbol Synchronizer block.
Error rate with symbol synchronization: 0.000 Error rate without symbol synchronization: 0.010
Extended Examples
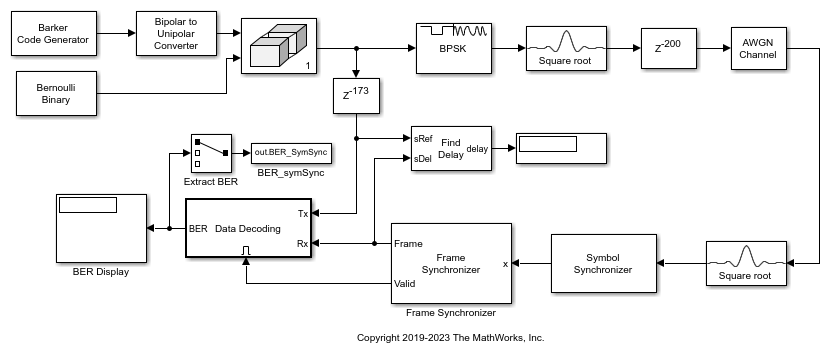
Frame Synchronization Using Barker Code Preamble
Use a length 13 Barker code frame preamble for frame synchronization of data bits.
Passband Modulation
Simulate passband modulation by multiplying a modulated complex signal with a complex sine wave to perform frequency upconversion.
Impact of RF Effects on Communication System Performance
Model thermal noise, phase noise, and nonlinearity impairments of an RF transceiver in Simulink®.
Ports
Input
Input signal, specified as a column vector or a Ki-by-N matrix. Ki is the number of input samples per signal channel, and N is the number of signal channels.
For a Ki-by-N matrix input, the object processes columns of the input matrix as N independent channels.
Data Types: single | double | fixed point
Output
Output signal, returned as a column vector or a Ko-by-N matrix. Ko is equal to Ki / Decimation factor. Ki is the number of input samples per signal channel, and N is the number of signal channels.
The block filters each channel over time and generates a Ko-by-N output matrix. The output signal is the same data type as the input signal.
Data Types: single | double | fixed point
Parameters
To edit block parameters interactively, use the Property Inspector. From the Simulink Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.
Main
Filter shape, specified as Square root or
Normal. For more information, see Filter Characteristics.
Roll-off factor of the filter, specified as a scalar in the range [0,
1].
Filter span in symbols, specified as an even positive integer. The block truncates the infinite impulse response length of the ideal raised cosine filter to an FIR with a length equal to the value of this parameter.
Number of input samples per symbol, specified as an integer value greater
than 1. This parameter defines the number of input
samples that represent one symbol in the input signal.
Decimation factor the block applies to the input signal, specified as a positive integer. The output samples per symbol equals the value of the input samples per symbol divided by the decimation factor. If the decimation factor is one, then the block only applies filtering and there is no decimation.
Decimation offset in samples, specified as an integer in the range
[0, (Decimation
factor – 1).
Linear filter gain, specified as a positive scalar. The block scales the normalized filter coefficients by the linear filter gain value that you specify.
Input processing control, specified as one of these options:
Columns as channels (frame based)— The block treats each column of the input as a separate channel.Elements as channels (sample based)— The block treats each element of the input as a separate channel.
Block processing rate for input signal downsampling and filtering, specified as one of these options:
Enforce single-rate processing— When you select this option, the block maintains the input sample rate and processes the signal by decreasing the output frame size by a factor of K.Allow multirate processing— When you select this option, the block processes the signal such that the output sample rate is K times slower than the input sample rate.
Dependencies
To use Enforce single-rate processing, you must set
Input processing to Columns as
channels (frame based).
Select this parameter to save the filter coefficients as the MATLAB® workspace variable that you specify in the Coefficient variable name parameter.
Name of coefficient variable to create in the MATLAB workspace.
Dependencies
This parameter appears when you select Export filter coefficients to workspace.
To analyze the raised cosine filter response, click the View Filter Response button. MATLAB opens a filter visualization window. When you change the block mask parameter settings, click the button again to open a new instance of the window and see the new filter characteristics. Previous filter visualization windows remain open and reflect your previous mask settings. Instances of the filter visualization window remain open after you close the model
Data Types
Select the rounding mode for fixed-point operations. The block uses
rounding mode when the result of a fixed-point calculation does not map
exactly to a number representable by the data type. The filter coefficients
do not obey this parameter; they always round to
Nearest. For more information, see Rounding Modes
or Rounding Mode: Simplest (Fixed-Point Designer).
Select the overflow mode for fixed-point operations. The filter coefficients do not obey this parameter; they are always saturated.
Specify the word length and the fraction length of the filter coefficients (numerator and denominator).
This block is a subsystem that contains a FIR Decimation block. For diagrams showing the use of the coefficient data types in this block, see the filter structure diagrams for the Discrete FIR Filter (Simulink) block.
When you select Inherit: Same word length as input, the word
length of the filter coefficients match that of the input to the block. In
this mode, the fraction length of the coefficients is automatically set to
the binary-point only scaling that provides you with the best precision
possible given the value and word length of the coefficients.
The filter coefficients do not obey the Rounding
mode and the Saturate on integer
overflow parameters; they are always saturated and rounded
to Nearest.
For information about specifying data types, see Data Type Assistant.
Specify the product output word and fraction lengths. For diagrams showing the use of the product output data type in this block, see the filter structure diagrams for the Discrete FIR Filter (Simulink) block and Multiplication Data Types.
When you select Inherit: Same as input, these characteristics
match those of the input to the block.
For information about specifying data types, see Data Type Assistant.
Specify the accumulator word and fraction lengths. For diagrams showing the use of the accumulator data type in this block, see the filter structure diagrams for the Discrete FIR Filter (Simulink) block and Multiplication Data Types.
When you select
Inherit: Same as input, these characteristics match those of the input to the block.When you select
Inherit: Same as product output, these characteristics match those of the product output.
For information about specifying data types, see Data Type Assistant.
Specify the output word and fraction lengths.
When you select
Inherit: Same as input, these characteristics match those of the input to the block.When you select
Inherit: Same as accumulator, these characteristics match those of the accumulator.
For information about specifying data types, see Data Type Assistant.
Select this parameter to prevent the fixed-point tools from overriding the data types that you specify in the block dialog box. For more information, see the Fixed-Point Tool (Fixed-Point Designer).
Block Characteristics
More About
The Data Type Assistant helps you set data
attributes. To use the Data Type Assistant, click ![]() . For more information, see Specify Data Types Using Data Type Assistant (Simulink).
. For more information, see Specify Data Types Using Data Type Assistant (Simulink).
Tips
Exporting Filter Coefficients to the MATLAB Workspace
To examine or manipulate the coefficients of the filter that this block designs, select Export filter coefficients to workspace. Set the Coefficient variable name parameter to the name of a variable that you want the block to create in the MATLAB workspace. Running the simulation causes the block to create the variable, overwriting any previous contents in case the variable already exists.
Algorithms
Characteristics of the raised cosine receive filter are the same as in the Raised Cosine Transmit Filter block, except that for the receive filter, the input response length of the filter depends on the value of the Input samples per symbol parameter.
The Filter
shape parameter determines which type of filter the block uses;
choices are Normal and Square
root.
The impulse response of a normal raised cosine filter with roll-off factor R and symbol period T is
The impulse response of a square root raised cosine filter with roll-off factor R is
The impulse response of a square root raised cosine filter convolved with itself is approximately equal to the impulse response of a normal raised cosine filter.
Unlike an ideal raised cosine filter, which has an infinite impulse response (IIR), the block is an FIR filter and truncates the impulse response to the number of symbols that the Filter span in symbols parameter specifies. The impulse response length of the filter is (L×N + 1), where N is the Filter span in symbols parameter value and L is the Input samples per symbol parameter value.
The Rolloff
factor, R, determines the excess bandwidth of the
filter. R must be in the range [0,
1]. For example, a roll-off factor of 0.5
means that the bandwidth of the filter is 1.5 times the input sampling
frequency.
The block normalizes the filter coefficients to unit energy. If you specify a
Linear amplitude
filter gain value other than 1, then the block
scales the normalized filter coefficients using the gain value you specify.
For information about the latency of the block, see details in FIR Decimation.
To have the block decimate the filtered signal, set the Decimation
factor parameter to a value greater than
1.
If K represents the Decimation factor parameter value, then the block retains 1 / K of the samples, choosing them as follows:
If the Decimation offset parameter is zero, then the block selects the samples of the filtered signal indexed by 1, K+1, 2*K+1, 3*K+1, ....
If the Decimation offset parameter is a positive integer less than the frame length,M, then the block initially discards that number of samples from the filtered signal and downsamples the remaining data as in the previous case.
To preserve the entire filtered signal and avoid decimation, set Decimation
factor to 1. This setting is appropriate
when the output from the filter block forms the input to a timing phase recovery
block, such as Symbol Synchronizer. The timing phase
recovery block performs the downsampling in that case.
This block accepts a column vector or matrix input signal.
If you set Decimation
factor to 1, then the input and output
signals share the same sampling mode, sample time, and vector length.
If you set Decimation factor to a value K,
greater than 1, then K and the input sampling
mode determine the characteristics of the output signal.
When you set the Rate options parameter to Enforce
single-rate processing, the input and output of the block have
the same sample rate. To generate the output while maintaining the input sample
rate, the block resamples the data in each column of the input such that the
frame size of the output (Mo) is 1 /
K times that of the input
(Mo =
Mi / K), In
this mode, the input frame size, Mi,
must be a multiple of K.
When you set the Rate options parameter to Allow
multirate processing, the input and output of the block are
the same size, but the sample rate of the output is K times
slower than that of the input. When the block is in multirate processing mode,
you must also specify a value for the Input processing parameter.
When you set the Input processing parameter to
Elements as channels (sample based), the block treats an M-by-N matrix input as M×N independent channels, and processes each channel over time. The output sample period (Tso) is K times longer than the input sample period (Tso = K×Tsi), and the input and output sizes are identical.When you set the Input processing parameter to
Columns as channels (frame based), the block treats an Mi-by-N matrix input as N independent channels. The block processes each column of the input over time by keeping the frame size constant (Mi=Mo), while making the output frame period (Tfo) K times longer than the input frame period (Tfo = K×Tfi).
To examine or manipulate the coefficients of the filter that this block designs, select Export filter coefficients to workspace. Then set the Coefficient variable name parameter to the name of a variable that you want the block to create in the MATLAB workspace. Running the simulation causes the block to create the variable, overwriting any previous contents in case the variable already exists.
Extended Capabilities
Generated code relies on memcpy or
memset functions (string.h) under certain
conditions.
This block supports SIMD code generation using Intel® AVX2 technology under these conditions:
Input processing is set to
Columns as channels (frame based).Rate options is set to
Enforce single-rate processing.Input signal is real-valued with real filter coefficients.
Input signal is complex-valued with real or complex filter coefficients.
Input signal has a data type of
singleordouble.
The SIMD technology significantly improves the performance of the generated code. For details, see Generate SIMD Code from Simulink Blocks for Intel Platforms (Embedded Coder).
HDL Coder™ provides additional configuration options that affect HDL implementation and synthesized logic.
This block is a subsystem that contains an FIR Decimation block. You can set HDL Properties on the subsystem, or you can look under the mask and set HDL Properties on the filter block. See the "HDL Code Generation" section of the Subsystem, Atomic Subsystem, CodeReuse Subsystem (Simulink) and FIR Decimation block reference pages for a list of properties.
To save setting changes under the mask, you must break the library link. To break the library link, select the Raised Cosine Receive Filter block and run this command.
set_param(gcb,'LinkStatus','inactive')
Version History
Introduced before R2006a
See Also
Apps
Blocks
Objects
Functions
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)