ofdmEqualize
Syntax
Description
[
returns equalized symbols eqsym,csi]= ofdmEqualize(rxsym,heff,nvar)eqsym and soft channel state information
csi after performing minimum mean squared error (MMSE) equalization
on input OFDM symbols rxsym. heff specifies the
effective estimated channel information. nvar specifies the estimated
noise variance.
Examples
Obtain the channel response for a beamformed OFDM signal with parallel data streams filtered through an -by- MIMO channel. Use the channel response to apply OFDM equalization to the received OFDM-demodulated signal.
Define simulation variables.
rng(1); numStreams = 2; % Number of parallel data streams (Ns) numTx = 4; % Number of transmit antennas (Nt) numRx = 3; % Number of receive antennas (Nr) bps = 6; % Bits per QAM symbol (and OFDM data subcarrier) nfft = 256; % FFT length cpLen = 16; % Cyclic prefix length numOFDMSym = 10; % Number of OFDM symbols SNRdB = 40; % Signal-to-noise ratio
Check that the number of data streams is no greater than either the number of transmit antennas or the number of receive antennas.
if numStreams > min(numTx,numRx) error('numStreams must be equal to or less than numTx and numRx.'); end
Configure OFDM subcarriers.
ofdmNullIdx = ... % Guard bands and DC subcarrier [1:9 (nfft/2+1) (nfft-8+1:nfft)]'; numDataSC = ... % Number of data subcarriers nfft-length(ofdmNullIdx);
Generate an array of data symbols consisting of parallel data streams, QAM-modulate the symbols, and then OFDM-modulate the QAM-modulated symbols.
dataBits = randi([0,1],[numDataSC*bps numOFDMSym numStreams]); M = 2^bps; % Modulation order qamTx = qammod(dataBits,M, ... InputType="bit", ... UnitAveragePower=true); ofdmOut = ofdmmod(qamTx,nfft,cpLen,ofdmNullIdx);
Beamforming expands the dimensionality of the transmit signal to improve link performance over multipath channels. The data streams are fed through a beamformer that focuses the transmit energy over an -by-1 transmit antenna array where the number of antennas .
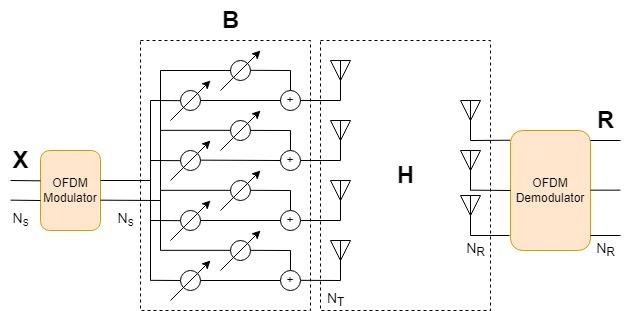
Form a beamformer matrix from steering vectors acting on each stream.
% Beamform the transmitted signal fc = 1e9; lambda = physconst('LightSpeed')/fc; beamAngles = 15; antIdx = (0:numTx-1); antDelay = 2*pi*sin(2*pi*beamAngles*(0:numStreams-1).'/360)/lambda; B = exp(1i*antIdx.*antDelay); % Ns x Nt beamformer matrix txOut = ofdmOut * B;
Filter the OFDM-modulated signal through a MIMO channel to get the channel coefficients.
mimoChannel = comm.MIMOChannel( ... SampleRate=1e6, ... PathDelays=[0 3e-6 5e-6], ... AveragePathGains=[0 0.5 0.2], ... MaximumDopplerShift=0, ... SpatialCorrelationSpecification="None", ... NumTransmitAntennas=numTx, ... NumReceiveAntennas=numRx, ... PathGainsOutputPort=true); [channelOut,pathGains] = mimoChannel(txOut);
In a practical system, the channel must be sounded to estimate the channel response. Instead of sounding, the ofdmChannelResponse function computes the exact channel response using the path gains and path filters that are available after you pass data through the MIMO channel System object. Use channel path gains returned by the MIMO channel object, and the path filters and timing offset returned by the info object function, to obtain the OFDM channel response. If , the channel forms an over-determined system (there are more receive antennas than necessary to adequately decode the transmitted signals). Call ofdmChannelResponse with the pathGains from the MIMO channel function to get the channel response.
mimoChannelInfo = info(mimoChannel); pathFilters = mimoChannelInfo.ChannelFilterCoefficients; toffset = mimoChannelInfo.ChannelFilterDelay; h = ofdmChannelResponse(pathGains,pathFilters,nfft,cpLen, ... setdiff(1:nfft,ofdmNullIdx),toffset); % Nsc x Nsym x Nt x Nr [rxIn,nVar] = awgn(channelOut,SNRdB,"measured");
Before demodulating the OFDM signal, account for the timing offset and symbol offset, remove the initial samples, and then pad with zeros to keep the signal length unchanged.
zeropadding = zeros(toffset,numRx); ofdmDemodIn = [rxIn(toffset+1:end,:); zeropadding]; symOffset = cpLen/2;
OFDM-demodulate and equalize the received signal.
rxSym = ofdmdemod(ofdmDemodIn,nfft,cpLen,symOffset,ofdmNullIdx);
The effects of beamforming and the MIMO channel affect the received data streams. The effective channel () is an -by- matrix defined as the product of the transmit beamformer and the MIMO channel coefficients.
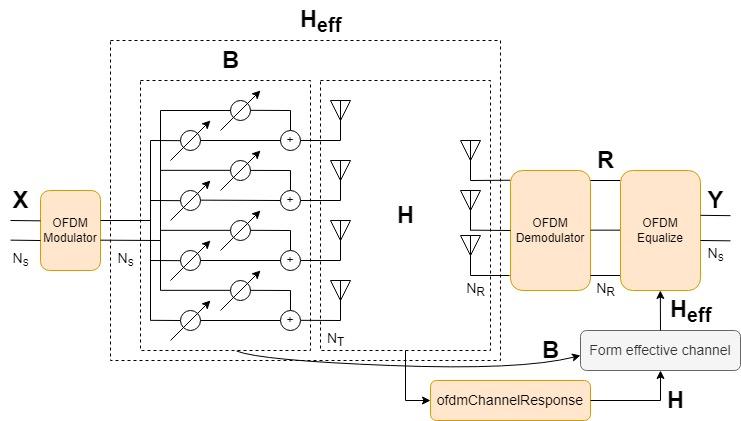
To use the OFDM channel response when equalizing the OFDM-demodulated signal, you must reshape the -by--by--by- array to an -by--by- array. Form the effective channel using the beamformer matrix B and the reshaped channel coefficients h. Equalize the received OFDM signal using the calculated effective channel, the noise variance, and the MMSE algorithm.
hReshaped = reshape(h,[],numTx,numRx); hEff = zeros(numDataSC*numOFDMSym,numStreams,numRx); for k = 1:numOFDMSym*numDataSC hEff(k,:,:) = B * squeeze(hReshaped(k,:,:)); end eqSym = ofdmEqualize(rxSym,hEff,nVar);
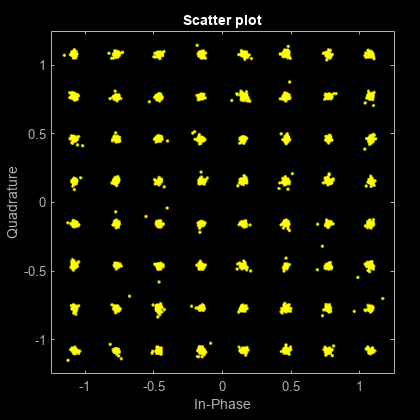
Show the received OFDM-demodulated symbols (rxSym) and the equalized OFDM-demodulated symbols (eqSym). The constellation of the OFDM-demodulated symbols before equalization does not resemble the QAM constellation. After equalization, the constellation points lay near the reference constellation.
figure(1); scatterplot(rxSym(:));

figure(2); scatterplot(eqSym(:));
Initialize variables for simulation of a MIMO system and a 120-resource-element subset of the OFDM subcarrier-symbol grid.
Nre = 120; % Number of resource elements Ns = 4; % Number of data streams Nr = 8; % Number of receive antennas nvar = 0.1; % Noise variance
Create random signals for a 2-D symbol array and a channel estimate.
rxsym2d = complex(randn(Nre,Nr),randn(Nre,Nr)); Hest = complex(randn(Nre,Ns,Nr),randn(Nre,Ns,Nr));
Apply OFDM equalization to the 2-D signal contained in an 120-by-8 symbol array.
[eqsym2d,csi2d] = ofdmEqualize(rxsym2d,Hest,nvar,DataFormat="2-D");Reshape the 2-D signal to a 30-by-4-by-8 symbol array. Apply OFDM equalization to the 3-D signal. Compare the results of OFDM equalization for the 30-by-4-by-8 symbol array with OFDM equalization for the 120-by-8 symbol array. As the isequal function result shows, the equalized symbols and soft channel state information returned for the 30-by-4-by-8 and 120-by-8 symbol arrays are equal.
rxsym3d = reshape(rxsym2d,30,4,Nr);
[eqsym3d,csi3d] = ofdmEqualize(rxsym3d,Hest,nvar,DataFormat="3-D");
isequal(eqsym3d,reshape(eqsym2d,30,4,Ns))ans = logical
1
isequal(csi3d,csi2d)
ans = logical
1
Reshape the 2-D signal to a 60-by-2-by-8 symbol array. Apply OFDM equalization to the 3-D signal. Compare the results of OFDM equalization for the 60-by-2-by-8 symbol array with OFDM equalization for the 120-by-8 symbol array. The isequal function result confirms the equalized symbols and soft channel state information returned for the 60-by-2-by-8 and 120-by-8 symbol arrays are equal.
rxsym3d2 = reshape(rxsym2d,60,2,Nr);
[eqsym3d2,csi3d2] = ofdmEqualize(rxsym3d2,Hest,nvar,DataFormat="3-D");
isequal(eqsym3d2,reshape(eqsym2d,60,2,Ns))ans = logical
1
isequal(csi3d2,csi2d)
ans = logical
1
Input Arguments
Received symbols, specified as a numeric array or a dlarray (Deep Learning Toolbox)
object. For more information, see Array Support.
If
DataFormatis set to"3-D", the function expectsrxsymto be specified as an NSC-by-NSymbols-by-NR array. NSC represents the number of OFDM subcarriers, NSymbols represents the number of OFDM symbols, and NR represents the number of receive antennas.If
DataFormatis set to"2-D", the function expectsrxsymto be specified as an NRE-by-NR array. NRE represents the number of resource elements in an irregular subset of the OFDM subcarrier symbol grid. A resource element comprises one subcarrier in the frequency domain and one OFDM symbol in the time domain.
Data Types: double | single
Complex Number Support: Yes
Effective channel estimate, specified as a 3-D numeric array, or a dlarray (Deep Learning Toolbox)
object. heff can be a dlarray object only when
the number of data streams NS == 1. For more information, see Effective Channel and Array Support.
If
DataFormatis set to"3-D", the function expectsheffto be an NSC-by-NS-by-NR or an (NSC×NSymbols)-by-NS-by-NR array.If
heffis an NSC-by-NS-by-NR array, all OFDM symbols inrxsymare equalized by the same channel estimate. NSC represents the number of OFDM subcarriers, NS represents the number of data streams, and NR represents the number of receive antennas.If
heffis an (NSC×NSymbols)-by-NS-by-NR array, each OFDM symbol inrxsymis equalized by the corresponding entry inheff. NSymbols represents the number of OFDM symbols.
If
DataFormatis set to"2-D", the function expectsheffto be an NRE-by-NS-by-NR array. Each OFDM symbol inrxsymis equalized by the corresponding entry inheff. NRE represents the number of resource elements in an irregular subset of the OFDM subcarrier symbol grid.
Data Types: double | single
Complex Number Support: Yes
Noise variance estimate for MMSE equalization, specified as a nonnegative scalar.
Dependencies
The noise variance setting is used only when you set
Algorithm to "mmse".
Data Types: double | single
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: ofdmEqualize(rxsym,heff,DataFormat="2-D") equalizes an
NRE-by-NR
input OFDM symbol array using the MMSE algorithm.
Equalization algorithm, specified as "mmse" or
"zf".
When this argument is set to
"mmse", the function equalizes using the MMSE algorithm.When this argument is set to
"zf", the function equalizes using the zero-forcing algorithm. When using the zero-forcing algorithm, thenvarargument value is ignored.
Format of the signals, specified as "3-D" or
"2-D".
When this argument is set to "3-D", OFDM subcarriers and OFDM
symbols use two separate dimensions in the representation of
rxsym and eqsym.
The
rxsyminput must be an NSC-by-NSymbols-by-NR array.The
eqsymoutput is returned as an NSC-by-NSymbols-by-NS array.
When this argument is set to "2-D", OFDM subcarriers and OFDM
symbols use one combined dimension in the representation of rxsym
and eqsym.
The
rxsyminput must be an NRE-by-NR array.The
eqsymoutput is returned as an NRE-by-NS array.
NSC represents the number of OFDM subcarriers. NSymbols represents the number of symbols. NRE represents the number of resource elements in an irregular subset of the OFDM subcarrier symbol grid. NS represents the number of data streams. NR represents the number of receive antennas.
Output Arguments
Equalized symbols, returned as a 3-D or 2-D numeric array, or a dlarray (Deep Learning Toolbox). For
more information, see Array Support.
If
DataFormatis set to"3-D", the function returns an NSC-by-NSymbols-by-NS array. NSC represents the number of OFDM subcarriers, NSymbols represents the number of OFDM symbols, and NS represents the number of data streams.If
DataFormatis set to"2-D", the function returns an NRE-by-NS array. NRE represents the number of resource elements in an irregular subset of the OFDM subcarrier symbol grid.
Soft channel state information, returned as a matrix with size(csi,1) =
size(heff,1) and size(csi,2) =
NS = size(heff,2).
NS represents the number of data streams.
This output is a log-likelihood ratio (LLR) scaling factor that accounts for the SNR in
each resource element. A resource element comprises one subcarrier in the frequency
domain and one OFDM symbol in the time domain.
The returned matrix can be a numeric array, or a dlarray (Deep Learning Toolbox). For
more information, see Array Support.
More About
The ofdmEqualize function supports input signals
represented in a numeric array, dlarray (Deep Learning Toolbox), or
gpuArray (Parallel Computing Toolbox). If inputs are specified as a
combination of dlarray and gpuArray, the returned
matrix is a dlarray object on the GPU.
The number of batch observations (NB) is an optional dimension that can be added to these inputs for all supported data types.
rxsym— The received symbols can be an:NSC-by-NSymbols-by-NR-by-NB array, if
DataFormatis specified as"3-D".NRE-by-NR-by-NB array, if
DataFormatis specified as"2-D".
heff— The channel estimate can be an:NSC-by-NS-by-NR-by-NB or (NSC×NSymbols)-by-NS-by-NR-by-NB array, if
DataFormatis specified as"3-D".NRE-by-NS-by-NR-by-NB array, if
DataFormatis specified as"2-D".
nvar— The noise variance can be a real vector with number of elements equal to number of batch observations, NB.
NSC is the number of OFDM subcarriers, NSymbols is the number of symbols, NRE is the number of resource elements in an irregular subset of the OFDM subcarrier symbol grid, NS is the number of data streams, and NR is the number of receive antennas.
For a list of Communications Toolbox™ features that support dlarray objects, see AI for Wireless.
Algorithms
Represent a MIMO, SISO, SIMO, or MISO communications system as Y = XHeff + N, where:
X is an NSC-by-NS transmitted signal.
Heff is an NS-by-NR MIMO channel matrix.
N is an NR-by-1 AWGN signal at receiver.
Y is an NSC-by-NR received signal.
NSC is the number of OFDM subcarriers.
NS is the number of data streams.
NR is the number of receive antennas.
In an OFDM system, Y = XHeff + N applies to each frequency subcarrier. Equalization estimates the transmitted OFDM signal X and the soft channel state information by using a zero-forcing (ZF) equalizer or a minimum mean square estimate (MMSE) equalizer.
With a ZF equalizer, the estimate of X is
where is the pseudo inverse of Ĥeff.
When NS < NR, the soft channel state information is
and when NS ≥ NR
With an MMSE equalizer, the estimate of X is
The soft channel state information is
The effective channel, Heff = PBH, measures the channel from the transmitted data streams to the receive antennas and results in an NS-by-NR matrix.
P is an NS-by-NS precoding matrix. When there is no precoding, the precoding matrix is an NS-by-NS identity matrix.
B is an NS-by-NT beamforming matrix. When there is no beamforming, NS=NT, and the beamforming matrix is an NS-by-NS identity matrix.
H is an NT-by-NR matrix containing the estimated channel information.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
Usage notes and limitations:
For the dimensions of input signals, if NS ≤ NR, then NR must not exceed 32. NS represents the number of data streams. NR represents the number of receive antennas.
This function supports GPU array inputs. For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Version History
Introduced in R2022bThe ofdmEqualize function adds support for C code generation with
input signals stored as dlarray (Deep Learning Toolbox)
objects.
The ofdmEqualize function adds support for dlarray (Deep Learning Toolbox) object
processing for deep learning applications.
The ofdmEqualize function adds support for gpuArray (Parallel Computing Toolbox) object processing to run code on a graphics processing unit
(GPU).
See Also
Functions
Objects
Blocks
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)