ofdmdemod
Demodulate using OFDM method
Syntax
Description
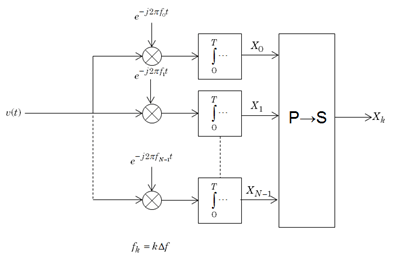
Y = ofdmdemod(X,nfft,cplen)X using
the orthogonal frequency division multiplexing (OFDM) method with an FFT size
specified by nfft and cyclic prefix length specified by
cplen. For information, see OFDM Demodulation.
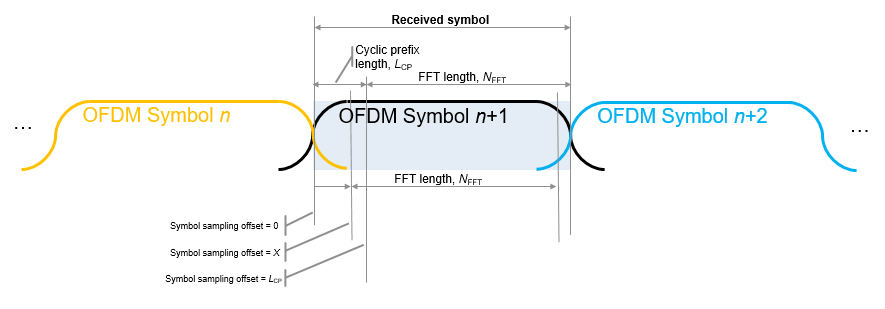
Y = ofdmdemod(X,nfft,cplen,symOffset,nullidx)nullidx. For this syntax, the symbol sampling offset is
applied to each OFDM symbol and the number of rows in the output is
nfft –
length(, which accounts for the
removal of null subcarriers. Use null subcarriers to account for guard bands and DC
subcarriers. For information, see Subcarrier Allocation and Guard Bands.nullidx)
[
returns pilot subcarriers for the pilot indices specified in
Y,pilots] = ofdmdemod(X,nfft,cplen,symOffset,nullidx,pilotidx)pilotidx. For this syntax, the symbol sampling offset is
applied to each OFDM symbol and number of rows in the output Y
is nfft –
length( –
nullidx)length(, which accounts for
the removal of null and pilot subcarriers. The function assumes that pilot
subcarrier locations are the same across each OFDM symbol and transmit
stream.pilotidx)
Y = ofdmdemod(X,nfft,cplen,___,OversamplingFactor=Value)OversamplingFactor×nfft) and
(OversamplingFactor×cplen) must both
result in integers. The default value for OversamplingFactor is
1.
For example, ofdmdemod(inSym,nfft,cplen,OversamplingFactor=2)
demodulates assuming the input signal was upsampled by a factor of two.
Tip
If you set the oversampling factor to a noninteger rational number, specify a fractional value
rather than a decimal value. For example, with an FFT length of 12 and an
oversampling factor of 4/3, their product is the integer
16. However, rounding 4/3 to
1.333 when setting the oversampling factor results in a noninteger
product of 15.9960, which results in a code error.