modwtLayer
Description
A MODWT layer computes the maximal overlap discrete wavelet transform (MODWT) and MODWT multiresolution analysis (MRA) of the input. Use of this layer requires Deep Learning Toolbox™.
Creation
Description
layer = modwtLayer'sym4').
The input to modwtLayer must be a real-valued dlarray (Deep Learning Toolbox) object in
"CBT" format. The size of the time dimension of the tensor input must
be greater than or equal to 2Level, where Level is the
transform level of the MODWT. modwtLayer formats the output as
"SCBT". For more information, see Layer Output Format.
Note
When you initialize the learnable parameters of modwtLayer, the
layer weights are set to the wavelet filters used in the MODWT. It is not recommended
to initialize the weights directly.
layer = modwtLayer(PropertyName=Value)layer = modwtLayer(Wavelet="haar") creates a MODWT layer that uses
the Haar wavelet. You can specify the wavelet and the level of decomposition, among
others.
Note
You cannot use this syntax to set the Weights
property.
Properties
MODWT
This property is read-only.
Name of an orthogonal wavelet used in the MODWT, specified as a character vector or a string scalar.
Orthogonal wavelets are designated as type 1 wavelets in the wavelet manager.
Valid built-in orthogonal wavelet families begin with 'haar',
'dbN',
'fkN',
'coifN',
'blN',
'hanSR.LP',
'symN', 'vaid', or
'beyl'. Use waveinfo with the wavelet family
short name to see supported values for any numeric suffixes and how to interpret those
values. For example, waveinfo("han").
For a wavelet specified by wname, the associated lowpass and
highpass filters Lo and Hi, respectively, are
[~,~,Lo,Hi] = wfilters(wname).
Data Types: char | string
This property is read-only.
Lowpass (scaling) filter, specified as an even-length real-valued vector.
LowpassFilter and HighpassFilter must have
equal length and correspond to the lowpass and highpass filters associated with an
orthogonal wavelet. You can use isorthwfb to determine
orthogonality.
[~,~,Lo,Hi] = wfilters("db2");
[tf,checks] = isorthwfb(Lo,Hi);[] and modwtLayer uses
Wavelet to determine the filters used in MODWT.You cannot specify both a wavelet name and a wavelet filter pair.
Example: layer =
modwtLayer('LowpassFilter',Lo,'HighpassFilter',Hi)
Data Types: single | double
This property is read-only.
Highpass (wavelet) filter, specified as an even-length real-valued vector.
LowpassFilter and HighpassFilter must have
equal length and correspond to the lowpass and highpass filters associated with an
orthogonal wavelet. You can use isorthwfb to determine orthogonality.
If unspecified, both filters default to [] and
modwtLayer uses Wavelet to determine the
filters used in MODWT.
You cannot specify both a wavelet name and a wavelet filter pair.
Data Types: single | double
This property is read-only.
Transform level to compute the MODWT, specified as a positive integer less than or
equal to floor(log2(N)), where
N is the size of the layer input in the time dimension.
Data Types: single | double
This property is read-only.
Boundary condition to use in the computation of the MODWT, specified as one of these:
"periodic"— The signal is extended periodically along the time dimension. The number of wavelet coefficients equals the size of the signal in the time dimension."reflection"— The signal is reflected symmetrically along the time dimension at the terminal end before computing the MODWT. The number of wavelet coefficients returned is twice the length of the input signal.
This property is read-only.
Selected levels for modwtLayer to output, specified as a vector
of positive integers less than or equal to Level.
Data Types: single | double
This property is read-only.
Include lowpass coefficients, specified as a numeric or logical
1 (true) or 0
(false). If specified as true, the MODWT layer
includes the Levelth level lowpass (scaling) coefficients in the
MODWT, or Levelth level smooth in the MODWTMRA.
Data Types: logical
This property is read-only.
Aggregate selected levels, specified as a numeric or logical 1
(true) or 0 (false). If
specified as true, the MODWT layer aggregates the selected levels
and lowpass level (if IncludeLowpass is true)
of each input channel by summation. If AggregateLevels is
true, the size of the output in the spatial dimension is
1. For more information, Compare modwtLayer Output with modwt and modwtmra Outputs.
Data Types: logical
This property is read-only.
Algorithm modwtLayer uses to compute the output, specified as
one of these:
"MODWTMRA"— Compute the maximal overlap discrete wavelet transform based multiresolution analysis."MODWT"— Compute the wavelet coefficients of the maximal overlap discrete wavelet transform.
For more information, see Comparing MODWT and MODWTMRA.
Layer
Layer weights, specified as [], a numeric array, or a
dlarray object.
The layer weights are learnable parameters.
You can use initialize (Deep Learning Toolbox)
to initialize the learnable parameters of a dlnetwork (Deep Learning Toolbox) that includes
modwtLayer objects. When you initialize the layers,
initialize sets Weights to the MODWT
wavelet filters associated with the specified Wavelet. For more
information, see Initialize Maximal Overlap Discrete Wavelet Transform Layer. (since R2025a)
It is not recommended to initialize the weights directly.
Data Types: single | double
Multiplier for weight learning rate, specified as a nonnegative scalar. If not
specified, this property defaults to zero, resulting in weights that do not update
with training. You can also set this property using the setLearnRateFactor (Deep Learning Toolbox) function.
The learnable parameter 'Weights' in
modwtLayer is a two-row matrix of the current filter pair. The
first row is the lowpass filter and the second row is the highpass filter. By default,
the weights are the lowpass and highpass filters associated with the default wavelet
and do not update.
Data Types: single | double
Layer name, specified as a character vector or a string scalar.
For Layer array input, the trainnet (Deep Learning Toolbox) and
dlnetwork (Deep Learning Toolbox) functions automatically assign
names to unnamed layers.
The modwtLayer object stores this property as a character vector.
Data Types: char | string
This property is read-only.
Number of inputs to the layer, stored as 1. This layer accepts a
single input only.
Data Types: double
This property is read-only.
Input names, stored as {'in'}. This layer accepts a single input
only.
Data Types: cell
This property is read-only.
Number of outputs from the layer, stored as 1. This layer has a
single output only.
Data Types: double
This property is read-only.
Output names, stored as {'out'}. This layer has a single output
only.
Data Types: cell
Examples
Create a MODWT layer to compute the multiresolution analysis for the input signal. Use a coiflet wavelet with order 5. Set the transform level to 8. Only keep the details at levels 3, 5, and 7, and the approximation.
layer = modwtLayer(Wavelet="coif5",Level=8, ... SelectedLevels=[3,5,7],Name="MODWT");
Create a dlnetwork object containing a sequence input layer, a MODWT layer, and an LSTM layer. For a level-8 decomposition, set the minimum sequence length to 2^8 samples. To work with an LSTM layer, a flatten layer is also needed before the LSTM layer to collapse the spatial dimension into the channel dimension.
mLength=2^8; sqLayer = sequenceInputLayer(1,Name="input",MinLength=mLength); layers = [sqLayer layer flattenLayer lstmLayer(10,Name="LSTM") ]; dlnet = dlnetwork(layers);
Run a batch of 10 random single-channel signals through the dlnetwork object. Inspect the size and dimensions of the output. The flatten layer has collapsed the spatial dimension.
dataout = forward(dlnet,dlarray(randn(1,10,2000,'single'),'CBT')); size(dataout)
ans = 1×3
10 10 2000
dims(dataout)
ans = 'CBT'
Load the Espiga3 electroencephalogram (EEG) dataset. The data consists of 23 channels of EEG sampled at 200 Hz. There are 995 samples in each channel. Save the multisignal as a dlarray, specifying the dimensions in order. dlarray permutes the array dimensions to the "CBT" shape expected by a deep learning network.
load Espiga3 [N,nch] = size(Espiga3); x = dlarray(Espiga3,"TCB");
Use modwt and modwtmra to obtain the MODWT and MRA of the multisignal down to level 6. By default, modwt and modwtmra use the sym4 wavelet.
lev = 6; wt = modwt(Espiga3,lev); mra = modwtmra(wt);
Compare with modwt
Create a MODWT layer that can be used with the data. Set the transform level to 6. Specify the layer to use MODWT to compute the output. By default, the layer uses the sym4 wavelet.
mlayer = modwtLayer(Level=lev,Algorithm="MODWT");Create a two-layer dlnetwork object containing a sequence input layer and the MODWT layer you just created. Treat each channel as a feature. For a level-6 decomposition, set the minimum sequence length to 2^6.
mLength = mlayer.Level;
sqInput = sequenceInputLayer(nch,MinLength=2^mLength);
layers = [sqInput
mlayer];
dlnet = dlnetwork(layers);Run the EEG data through the forward method of the network.
dataout = forward(dlnet,x);
The modwt and modwtmra functions return the MODWT and MRA of a multichannel signal as a 3-D array. The first, second, and third dimensions of the array correspond to the wavelet decomposition level, signal length, and channel, respectively. Convert the network output to a numeric array. Permute the dimensions of the network output to match the function output. Compare the network output with the modwt output.
q = extractdata(dataout); q = permute(q,[1 4 2 3]); max(abs(q(:)-wt(:)))
ans = 8.4402e-05
Choose a MODWT result from modwtLayer. Compare with the corresponding channel in the EEG data. Plot each level of the modwtLayer output. Different levels contain information about the signal in different frequency ranges. The levels are not time aligned with the original signal because the layer uses the MODWT algorithm.
channel = 10; t = 100:400; subplot(lev+2,1,1) plot(t,Espiga3(t,channel)) ylabel("Original EEG") for k=2:lev+1 subplot(lev+2,1,k) plot(t,q(k-1,t,channel)) ylabel(["Level ",k-1," of MODWT"]) end subplot(lev+2,1,lev+2) plot(t,q(lev+1,t,channel)) ylabel(["Scaling","Coefficients","of MODWT"]) set(gcf,Position=[0 0 500 700])

Compare with modwtmra
Create a second network similar to the first network, except this time specify that modwtLayer use the MODWTMRA algorithm and aggregate the fourth, fifth, and sixth levels. Do not include the lowpass level in the aggregation.
sLevels = [4 5 6]; mlayer = modwtLayer(Level=lev, ... SelectedLevels=sLevels, ... IncludeLowpass=0, ... AggregateLevels=1); layers = [sqInput mlayer]; dlnet2 = dlnetwork(layers);
Run the EEG data through the forward method of the network. Convert the network output to a numeric array. Permute the dimensions as done previously.
dataout = forward(dlnet2,x); q = extractdata(dataout); q = permute(q,[1 4 3 2]);
Aggregate the fourth, fifth, and sixth levels of the MRA. Compare with the network output.
mraAggregate = sum(mra(sLevels,:,:)); max(abs(q(:)-mraAggregate(:)))
ans = 2.1036e-04
Inspect a MODWTMRA result from the layer. Compare with the corresponding channel in the EEG data. By choosing only the fourth, fifth, and six levels, and not including the lowpass component, the layer removes several high and low frequency components from the signal. The transformed signal is smoother than the original signal and the low frequency components are removed so that the offset is closer to 0. The output is time aligned with the original signal because the layer uses the default MODWTMRA algorithm. Depending on your goal, preserving time alignment can be useful.
channel = 10; t = 100:400; figure hold on plot(t, Espiga3(t,channel)) plot(t,q(1,t,1,channel)) hold off legend(["Original EEG", "Layer Output"], ... Location="northwest")

Since R2025a
Initialize maximal overlap discrete wavelet transform (MODWT) layer weights to wavelet filter and scaling function, update deep learning neural network, and reset learnable parameters.
Define an array of seven layers: a sequence input layer, a MODWT layer, a 2-D convolutional layer, a batch normalization layer, a rectified linear unit (ReLU) layer, a fully connected layer, and a softmax layer. There is one feature in the sequence input. Set the minimum signal length in the sequence input layer to 500 samples. Configure the MODWT layer to compute the MODWT down to level 7 using the Daubechies wavelet of order 10.
wName = "db10"; layers = [ sequenceInputLayer(1,MinLength=500) modwtLayer(Level=7,Wavelet=wName,Name="modwt") convolution2dLayer(2,10,Padding="same") batchNormalizationLayer reluLayer fullyConnectedLayer(3) softmaxLayer];
Create a deep learning neural network from the layer array. By default, the dlnetwork function initializes the network at creation. For reproducibility, use the default random number generator.
rng("default")
net = dlnetwork(layers);Display the table of learnable parameters. The network weights and bias are nonempty dlarray objects.
tInit1 = net.Learnables
tInit1=7×3 table
Layer Parameter Value
___________ _________ __________________
"modwt" "Weights" {2×20 dlarray}
"conv" "Weights" {2×2×1×10 dlarray}
"conv" "Bias" {1×1×10 dlarray}
"batchnorm" "Offset" {1×10 dlarray}
"batchnorm" "Scale" {1×10 dlarray}
"fc" "Weights" {3×80 dlarray}
"fc" "Bias" {3×1 dlarray}
Compare the initialized weights of the MODWT layer from the list of learnable parameters with the scaling functions and wavelet filters of the specified wavelet. The modwtLayer weights are single precision and initialized to the specified wavelet.
[~,~,scale,wfilt] = wfilters(wName);
scLayer = tInit1.Value{1}(1,:);
ftLayer = tInit1.Value{1}(2,:);
[isequal(single(scale),scLayer) isequal(single(wfilt),ftLayer)]ans = 1×2 logical array
1 1
Set the learnable parameters to empty arrays.
net = dlupdate(@(x)[],net); net.Learnables
ans=7×3 table
Layer Parameter Value
___________ _________ ____________
"modwt" "Weights" {0×0 double}
"conv" "Weights" {0×0 double}
"conv" "Bias" {0×0 double}
"batchnorm" "Offset" {0×0 double}
"batchnorm" "Scale" {0×0 double}
"fc" "Weights" {0×0 double}
"fc" "Bias" {0×0 double}
Reinitialize the network. Display the network and the learnable parameters. The network weights and bias are nonempty dlarray objects.
net = initialize(net); tInit2 = net.Learnables
tInit2=7×3 table
Layer Parameter Value
___________ _________ __________________
"modwt" "Weights" {2×20 dlarray}
"conv" "Weights" {2×2×1×10 dlarray}
"conv" "Bias" {1×1×10 dlarray}
"batchnorm" "Offset" {1×10 dlarray}
"batchnorm" "Scale" {1×10 dlarray}
"fc" "Weights" {3×80 dlarray}
"fc" "Bias" {3×1 dlarray}
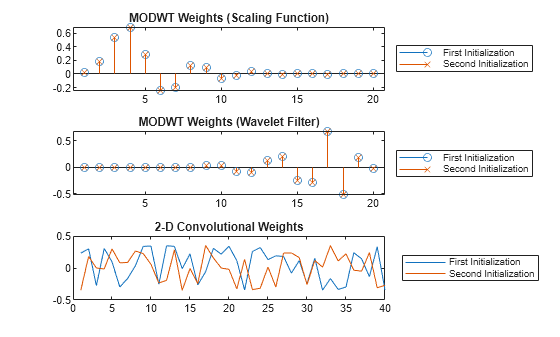
Compare the weights from the MODWT and 2-D convolutional layers along the two initialization calls. The MODWT layer sets the weights using the scaling and wavelet filters from the specified wavelet, while the convolutional layer weights consists of a new set of random values.
lgn = ["First" "Second"] + " Initialization"; weights1 = extractdata(tInit1.Value{1}); weights2 = extractdata(tInit2.Value{1}); tiledlayout vertical nexttile stem(weights1(1,:)) hold on stem(weights2(1,:),"x") hold off title("MODWT Weights (Scaling Function)") legend(lgn,Location="eastoutside") nexttile stem(weights1(2,:)) hold on stem(weights2(2,:),"x") hold off title("MODWT Weights (Wavelet Filter)") legend(lgn,Location="eastoutside") nexttile plot([tInit1.Value{2}(:) tInit2.Value{2}(:)]) title("2-D Convolutional Weights") legend(lgn,Location="eastoutside")
More About
modwtLayer formats the output as
"SCBT", a sequence of 1-D images where the image height corresponds to
the level of the wavelet transform, the second dimension corresponds to the channel, the
third dimension corresponds to the batch, and the fourth dimension corresponds to time. The
kth row, where k ≤ Level, contains the kth level detail of the
signal. The (th row contains the
Level+1)Levelth level smooth of the signal.
You can feed the output of
modwtLayerunchanged to a 1-D convolutional layer when you want to convolve along the level ("S") dimension. For more information, seeconvolution1dLayer(Deep Learning Toolbox).To feed the output of
modwtLayerto a 1-D convolutional layer when you want to convolve along the time ("T") dimension, you must place a flatten layer after themodwtLayer. For more information, seeflattenLayer(Deep Learning Toolbox).You can feed the output of
modwtLayerunchanged to a 2-D convolutional layer when you want to convolve along the level ("S") and time ("T") dimensions jointly. For more information, seeconvolution2dLayer(Deep Learning Toolbox).To use
modwtLayeras part of a recurrent neural network, you must place a flatten layer after themodwtLayer. For more information, seelstmLayer(Deep Learning Toolbox) andgruLayer(Deep Learning Toolbox).To use the output of
modwtLayerwith a fully connected layer as part of a classification workflow, you must reduce the time ("T") dimension of the output so that it is of size 1. To reduce the time dimension of the output, place a global pooling layer before the fully connected layer. For more information, seeglobalAveragePooling2dLayer(Deep Learning Toolbox) andfullyConnectedLayer(Deep Learning Toolbox).
Extended Capabilities
Usage notes and limitations:
The input signal to the
predictfunction must be fixed size.You can generate generic C/C++ code that does not depend on third-party libraries and deploy the generated code to hardware platforms.
Usage notes and limitations:
The input signal to the
predictfunction must be fixed size.You can generate CUDA code that is independent of deep learning libraries and deploy the generated code to platforms that use NVIDIA® GPU processors.
Version History
Introduced in R2022bStarting in R2025a, you can use initialize (Deep Learning Toolbox) to
initialize learnable parameters for deep learning neural networks that include
modwtLayer objects.
Starting in R2025a, the default value of the Weights property is
[]. Prior to R2025a, modwtLayer set the default value
to the wavelet filters used in the MODWT.
The modwtLayer object supports:
C/C++ code generation. You must have MATLAB® Coder™ to generate C/C++ code.
Code generation for NVIDIA GPUs. You must have GPU Coder™ to generate GPU code.
See Also
Apps
- Deep Network Designer (Deep Learning Toolbox)
Functions
Objects
cwtLayer|stftLayer(Signal Processing Toolbox) |dlarray(Deep Learning Toolbox) |dlnetwork(Deep Learning Toolbox)
Topics
- Practical Introduction to Multiresolution Analysis
- Comparing MODWT and MODWTMRA
- Deep Learning in MATLAB (Deep Learning Toolbox)
- List of Deep Learning Layers (Deep Learning Toolbox)
- Networks and Layers Supported for Code Generation (MATLAB Coder)
- Supported Networks, Layers, and Classes (GPU Coder)
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)