isbiorthwfb
Syntax
Description
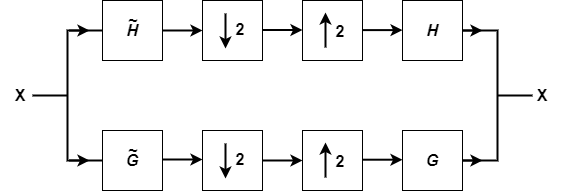
tf = isbiorthwfb(LoR,LoD)LoR and LoD satisfy the necessary and sufficient
conditions to be a two-channel biorthogonal perfect reconstruction (PR) wavelet filter bank.
isbiorthwfb forms the dual highpass (wavelet) filters using the
qmf function:
HiD = qmf(LoR)HiR = qmf(LoD)
For a list of the necessary and sufficient conditions that the lowpass and highpass filters must satisfy, see Biorthogonal Perfect Reconstruction Wavelet Filter Bank.
Examples
Input Arguments
Output Arguments
More About
References
[1] Strang, Gilbert, and Truong Nguyen. Wavelets and Filter Banks. Rev. ed. Wellesley, Mass: Wellesley-Cambridge Press, 1997.
[2] Burrus, C. S., Ramesh A. Gopinath, and Haitao Guo. Introduction to Wavelets and Wavelet Transforms: A Primer. Upper Saddle River, N.J: Prentice Hall, 1998.
Extended Capabilities
Version History
Introduced in R2022b