This example shows how to create a quadrature mirror filter associated with the db10 wavelet.
Obtain the scaling filter associated with the db10 wavelet.
dbwavf normalizes the filter coefficients so that the norm is equal to . Normalize the coefficients so that the filter has norm equal to 1.
Obtain the wavelet filter coefficients by using qmf. Plot the filters.
Save the current extension mode. Set the extension mode to Periodization. Generate a random signal of length 64. Perform a single-level wavelet decomposition of the signal using G and H. For purposes of reproducibility, set the random seed to the default value.
The lengths of the approximation and detail coefficients are both 32. Confirm that the filters preserve energy.
ans = 1×2
92.6872 92.6872
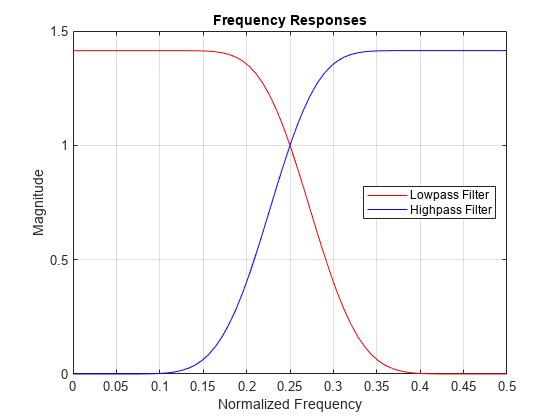
Compute the frequency responses of G and H. Zeropad the filters when taking the Fourier transform.
Plot the magnitude of each frequency response.
Confirm the sum of the squared magnitudes of the frequency responses of G and H at each frequency is equal to 2.
Confirm that the filters are orthonormal.
id = 2×2
1.0000 0.0000
0.0000 1.0000
Restore the original extension mode.