idwt2
Single-level 2-D inverse discrete wavelet transform
Syntax
Description
x = idwt2(cA,cH,cV,cD,wname)cA and details matrices
cH, cV, and
cD (horizontal, vertical, and diagonal, respectively)
using the wavelet specified by wname. For additional
information, see dwt2.
Let sa = size(, and let cA) =
size(cH) = size(cV) =
size(cD)lf
equal the length of the reconstruction filters associated with
wname. If the DWT extension mode is set to
periodization, the size of x, sx is
equal to 2*sa. For other extension modes, sx =
2*sa-lf+2. For additional information, see dwtmode.
x = idwt2(___,s)s central portion of the reconstruction
using any of the previous syntaxes.
x = idwt2(cA,[],[],[],___)x based on the approximation coefficients matrix
cA.
x = idwt2([],cH,[],[],___)x based on horizontal detail coefficients matrix
cH.
x = idwt2([],[],cV,[],___)x based on vertical detail coefficients matrix
cV.
Examples
Input Arguments
Tips
Algorithms
The 2-D wavelet reconstruction algorithm for images is similar to the one-dimensional case. The two-dimensional wavelet and scaling functions are obtained by taking the tensor products of the one-dimensional wavelet and scaling functions. This kind of two-dimensional inverse DWT leads to a reconstruction of approximation coefficients at level j from four components: the approximation at level j+1, and the details in three orientations (horizontal, vertical, and diagonal). The following chart describes the basic reconstruction steps for images.
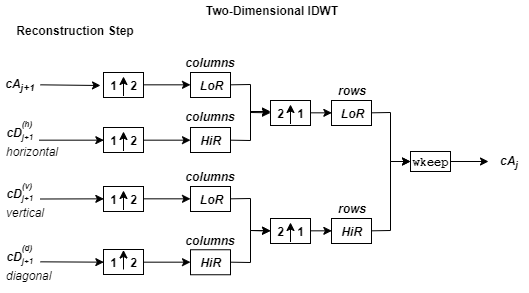
where
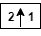 — Upsample columns: insert zeros at odd-indexed
columns
— Upsample columns: insert zeros at odd-indexed
columns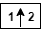 — Upsample rows: insert zeros at odd-indexed rows
— Upsample rows: insert zeros at odd-indexed rows — Convolve with filter X the rows of
the entry
— Convolve with filter X the rows of
the entry — Convolve with filter X the columns
of the entry
— Convolve with filter X the columns
of the entry
References
[1] Daubechies, Ingrid. Ten Lectures on Wavelets. CBMS-NSF Regional Conference Series in Applied Mathematics 61. Philadelphia, Pa: Society for Industrial and Applied Mathematics, 1992.
[2] Mallat, S.G. “A Theory for Multiresolution Signal Decomposition: The Wavelet Representation.” IEEE Transactions on Pattern Analysis and Machine Intelligence 11, no. 7 (July 1989): 674–93. https://doi.org/10.1109/34.192463.
[3] Meyer, Y. Wavelets and Operators. Translated by D. H. Salinger. Cambridge, UK: Cambridge University Press, 1995.
Extended Capabilities
Version History
Introduced before R2006a