mdscale
Nonclassical multidimensional scaling
Syntax
Description
Y = mdscale(D,p)n-by-n dissimilarity matrix D,
and returns an n-by-p configuration matrix. The rows
of Y correspond to the coordinates of n points in
p-dimensional space. The Euclidean distances between the points in
Y approximate a monotonic transformation of the corresponding
dissimilarities in D. By default, mdscale uses
Kruskal's normalized stress formula 1 criterion. To perform metric multidimensional scaling,
specify the Criterion name-value
argument.
Y = mdscale(___,Name=Value)
[
additionally returns the disparities, which are a monotonic transformation of the
dissimilarities in Y,stress,disparities]= mdscale(___)D.
Examples
Perform nonmetric and metric scaling on the same data set.
Load the cereal data set, which contains nutritional information for 77 cereals.
load cerealTake a subset of the data that consists of selected measurements of cereals from a single manufacturer.
X = [Calories,Protein,Fat,Sodium,Fiber, ... Carbo,Sugars,Shelf,Potass,Vitamins]; X = X(strcmp("K",cellstr(Mfg)),:); size(X)
ans = 1×2
23 10
X contains 23 observations and 10 predictor variables.
Create a dissimilarity matrix using the pdist function.
dissimilarities = pdist(X)
dissimilarities = 1×253
122.2784 322.6329 288.6226 347.3615 204.0662 295.9206 322.6050 303.9539 342.0409 141.1241 288.2603 263.6001 214.4808 293.1996 206.9734 248.1290 293.2388 107.3126 334.9910 289.9034 340.9883 269.9685 306.9267 335.2238 320.2312 180.7291 316.7823 306.8843 317.1183 274.2408 186.4457 288.6451 264.9925 203.6566 303.0380 234.1880 245.6135 349.3895 134.7739 264.2593 336.9481 304.9607 295.9307 166.1174 36.5240 131.1297 96.1613 1.4142 75.2994 143.8332
size(squareform(dissimilarities))
ans = 1×2
23 23
dissimilarities is a row vector that contains the 253 upper triangle elements of the dissimilarity matrix, which has size 23-by-23.
Use nonmetric scaling to recreate the data in two dimensions.
[Y,~,disparities] = mdscale(dissimilarities,2); distances = pdist(Y);
Visualize the results using a Shepard plot.
[~,ord] = sortrows([disparities(:),dissimilarities(:)]); plot(dissimilarities,distances,"o", ... dissimilarities(ord),disparities(ord),".-"); axis square xlim([0 max(dissimilarities)]); ylim([0 max(dissimilarities)]); xlabel("Dissimilarities") ylabel("Distances/Disparities") legend(["Distances","Disparities"],Location="northwest");

The x coordinates of the blue circles correspond to their original dissimilarity values, and the y coordinates correspond to their Euclidean distances in two-dimensional space. Most points lie close to the 1:1 line, indicating that a two-dimensional scaling provides a reasonably good representation of the higher-dimensional dissimilarities. The connected red points indicate the disparity values, which are a monotonic transformation of the dissimilarities.
Perform metric scaling on the same dissimilarities using the metricsstress criterion.
[Y,stress] = mdscale(dissimilarities,2,Criterion="metricsstress");
distances = pdist(Y);Visualize the results using a Shepard plot. Because there are no dissimilarities in metric scaling, plot a red 1:1 line.
plot(dissimilarities,distances,"o", ... [0 max(dissimilarities)],[0 max(dissimilarities)],".-") %xlim([0 max(dissimilarities)]); axis square; xlim([0 max(dissimilarities)]); ylim([0 max(dissimilarities)]); xlabel("Dissimilarities") ylabel("Distances")

Most points lie very close to the 1:1 line, indicating that a two-dimensional metric scaling provides a good representation of the higher-dimension dissimilarities.
This example shows how to perform nonmetric multidimensional scaling using mdscale.
Metric multidimensional scaling (MDS) creates a configuration of points whose interpoint distances approximate the given dissimilarities. This is sometimes too strict a requirement, and nonmetric scaling provides a less strict alternative. Instead of trying to approximate the dissimilarities themselves, nonmetric scaling approximates a nonlinear, but monotonic, transformation of them. Because of the monotonicity, larger or smaller distances on a plot of the output will correspond to larger or smaller dissimilarities, respectively. However, the nonlinearity implies that mdscale only attempts to preserve the ordering of dissimilarities. Thus, there may be contractions or expansions of distances at different scales.
Load the cereal data set, which contains measurements of 10 variables describing 77 breakfast cereals.
rng(0,"twister"); % For reproducibility load cereal
Take a subset of the data that consists of selected measurements of cereals from a single manufacturer.
X = [Calories Protein Fat Sodium Fiber ... Carbo Sugars Shelf Potass Vitamins]; X = X(strcmp("G",cellstr(Mfg)),:); size(X)
ans = 1×2
22 10
X contains 22 observations and 10 predictor variables.
Use pdist to transform the 10-dimensional data into dissimilarities. First standardize the cereal data, and use city block distance as a dissimilarity.
dissimilarities = pdist(zscore(X),'cityblock');
size(dissimilarities)ans = 1×2
1 231
The output from pdist is a symmetric dissimilarity matrix, stored as a vector containing only the (22*21/2) elements in its upper triangle. The choice of transformation to dissimilarities is application-dependent, and is made here only for simplicity. In some applications, the original data is already in the form of dissimilarities.
Use mdscale to perform nonmetric multidimensional scaling with Kruskal's stress formula 1 model.
[Y,stress,disparities] = mdscale(dissimilarities,2,Criterion="stress");
stressstress = 0.1562
The nonmetric stress criterion is a common method for computing the output; for more choices, see the mdscale reference page in the online documentation. The second output from mdscale is the value of that criterion evaluated for the output configuration. It is a measure of how well the inter-point distances of the output configuration approximate the disparities. The disparities are returned in the third output. They are the monotonically transformed values of the original dissimilarities.
Visualize these data to check the fit of the output configuration to the dissimilarities and to understand the disparities.
distances = pdist(Y); [dum,ord] = sortrows([disparities(:) dissimilarities(:)]); plot(dissimilarities,distances,"bo",dissimilarities(ord),... disparities(ord),"r.-",[0 25],[0 25],"k--") axis square; xlabel("Dissimilarities") ylabel("Distances/Disparities") legend({"Distances" "Disparities" "1:1 Line"},... "Location","NorthWest");
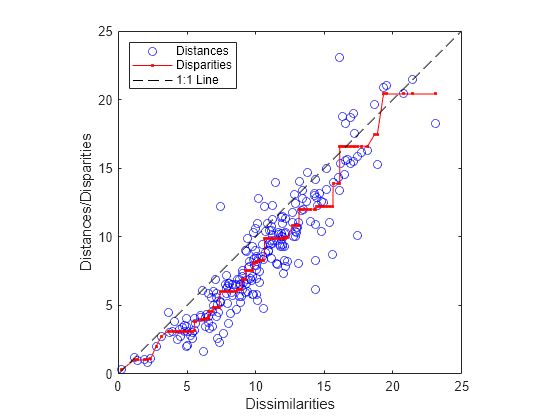
mdscale finds a configuration of points in two dimensions whose inter-point distances approximates the disparities, which in turn are a nonlinear transformation of the original dissimilarities. The concave shape of the disparities as a function of the dissimilarities indicates that fit tends to contract small distances relative to the corresponding dissimilarities. This might be perfectly acceptable in practice.
mdscale uses an iterative algorithm to find the output configuration, and the results can often depend on the starting point. By default, mdscale uses cmdscale to construct an initial configuration, and this choice often leads to a globally best solution. However, it is possible for mdscale to return a configuration that is a local minimum of the criterion. Such cases can be diagnosed and often overcome by running mdscale multiple times with different starting points. You can do this using the Start and Replicates name-value arguments.
Repeat the scaling, this time using five replicates of MDS, each starting at a different randomly-chosen initial configuration. mdscale displays a final stress criterion for each replication, and returns the configuration with the best fit.
[Y,stress] = mdscale(dissimilarities,2,Criterion="stress",... Start="random",Replicates=5, ... Options=statset(Display="final"));
35 iterations, Final stress criterion = 0.156209 31 iterations, Final stress criterion = 0.156209 48 iterations, Final stress criterion = 0.171209 33 iterations, Final stress criterion = 0.175341 32 iterations, Final stress criterion = 0.185881
Notice that mdscale finds several different local solutions, some of which do not have as low a stress value as the solution found with the cmdscale starting point.
Input Arguments
Dissimilarity matrix for n points, specified as an
n-by-n numeric matrix. You can also specify
D as a 1-by-k numeric vector that contains the
n*(n-1)/2 upper triangle elements of the dissimilarity matrix. In
this case, the software converts D into a square matrix using the
squareform function. The software treats
NaNs as missing values and ignores them. D
cannot contain any negative or Inf values, and must be one of the
following matrix types:
| Matrix Type | Symmetric | Description |
|---|---|---|
| Full dissimilarity | Yes | Zeros along the diagonal, and nonnegative dissimilarity values off the diagonal |
| Full dissimilarity (upper triangle form) | No | Nonnegative dissimilarity values above the diagonal, and zeros elsewhere |
| Full similarity | Yes |
|
Data Types: single | double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: mdscale(D,2,Criterion="sammon")
Goodness-of-fit criterion to minimize, specified as one of the values in the
following table. This argument also determines the type of scaling that
mdscale performs. In metric scaling, the interpoint distances in
Y approximate the dissimilarities in D. In
nonmetric scaling, the interpoint distances in Y approximate the
disparities, which are a monotonic transformation of the
dissimilarities in D.
| Value | Scaling Type | Description |
|---|---|---|
"stress" (default) | Nonmetric | Stress normalized by the sum of squares of the interpoint distances, also known as Kruskal's stress formula 1 [4] |
"sstress" | Nonmetric | Squared stress, normalized with the sum of 4th powers of the interpoint distances. This criterion is more sensitive to large discrepancies between points than stress formula 1. |
"metricstress" | Metric | Stress, normalized with the sum of squares of the dissimilarities |
"metricsstress" | Metric | Squared stress, normalized with the sum of 4th powers of the dissimilarities |
"sammon" | Metric | Sammon's nonlinear mapping criterion. Unlike Kruskal's stress formula 1, which treats all distances equally, Sammon's criterion emphasizes the preservation of small distances. This can make the algorithm more computationally intensive and slower to converge [5]. |
"strain" | Metric | A criterion equivalent to that used in classical multidimensional scaling |
Example: Criterion="sstress"
Data Types: char | string
Dissimilarity weights, specified as an
n-by-n symmetric numeric matrix of nonnegative
values, or a 1-by-n*(n-1)/2 numeric vector of nonnegative values,
where n is the number of points in D.
Weights must have the same size as D. When
mdscale computes and minimizes stress, it weighs the
elements of D with the corresponding values in
Weights. The software effectively ignores any elements of
D with a corresponding zero weight value.
Note
When you specify weights as a full matrix, its diagonal elements are ignored
and have no effect, since the corresponding diagonal elements of
D do not enter into the stress calculation.
Data Types: single | double
Method for selecting initial configuration of points for Y,
specified as one of the values in this table.
| Value | Description |
|---|---|
"cmdscale" (default) | The software constructs an initial classical multidimensional scaling
configuration using the cmdscale function. This value
is not valid when you specify Weights and at least one
weight value is zero. |
"random" | The software chooses point locations randomly from an appropriately
scaled p-dimensional normal distribution with
uncorrelated coordinates. |
| numeric matrix | An n-by-p matrix of initial
locations, where n is the number of points in D. In this
case, when you specify p=[], the software infers
p from the second dimension of the matrix. You can also
specify Start as a 3-D array that contains multiple
initial configurations. In this case, if you do not specify
Replicates, the software sets
Replicates to the size of the array's third
dimension. |
Tip
To reduce the likelihood that the software finds only a local minimum solution,
try running mdscale multiple times with different starting
points, and specify a larger value of Replicates.
Example: Start="random"
Data Types: char | string | single | double
Number of times to repeat the scaling, specified as a nonnegative integer. If you
do not specify Start, the software sets
Replicates=1. If you specify Start as a
3-D array:
Replicatesmust equal the size of the array's third dimension.If you do not specify
Replicates, the software setsReplicatesto the size of the array's third dimension.
At each iteration, mdscale uses a new initial
configuration. You can specify this argument to reduce the likelihood that
mdscale finds only a local minimum solution.
Example: Replicates=3
Data Types: single | double
Options for the iterative fitting criterion minimization algorithm, specified as a
structure. Create the Options structure using statset. This table lists the option fields and their
values.
| Field Name | Value | Default |
|---|---|---|
Display | Amount of information to display, specified as one of the following:
| "off" |
MaxIter | Maximum number of iterations, specified as a positive integer. | 200 |
TolFun | Termination tolerance for the stress criterion and its gradient, specified as a positive scalar value. | 1e-4 |
TolX | Termination tolerance for the configuration location step size, specified as a positive scalar value. | 1e-4 |
Example: Options=statset(Display="final",
MaxIter=10)
Data Types: struct
Output Arguments
Stress evaluated at Y, returned as a numeric scalar. For
nonmetric scaling (the default), the stress value is a measure of how well the
interpoint distances of the output configuration matrix Y
approximate the disparities. For metric scaling,
the stress value is a measure of how well the interpoint distances of the output
configuration matrix approximate the input dissimilarities
D.
Disparities, returned as a numeric matrix of the same size as
D. For nonmetric scaling, the disparities are the monotonic
transformed values of the dissimilarities in D. For metric scaling,
there are no disparities, and mdscale returns
D.
References
[1] Cox, Trevor F., and Michael A. A. Cox. Multidimensional Scaling. 2nd ed. Monographs on Statistics and Applied Probability 88. Boca Raton: Chapman & Hall/CRC, 2001.
[2] Davison, Mark L. Multidimensional Scaling. Wiley Series in Probability and Mathematical Statistics. New York: Wiley, 1983.
[3] Kruskal, J. B. “Multidimensional Scaling by Optimizing Goodness of Fit to a Nonmetric Hypothesis.” Psychometrika 29, no. 1 (March 1964): 1–27.
[4] Kruskal, J. B. “Nonmetric Multidimensional Scaling: A Numerical Method.” Psychometrika 29, no. 2 (June 1964): 115–29. https://doi.org/10.1007/BF02289694.
[5] Sammon, J.W. “A Nonlinear Mapping for Data Structure Analysis.” IEEE Transactions on Computers C–18, no. 5 (May 1969): 401–9.
[6] Seber, G. A. F. Multivariate Observations. 1st ed. Wiley Series in Probability and Statistics. Wiley, 1984.
Version History
Introduced before R2006a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)