procrustes

Procrustes analysis

Syntax

d = procrustes(X,Y)

d = procrustes(X,Y,Name,Value)

[d,Z] = procrustes(___)

[d,Z,transform] = procrustes(___)

Description

d = procrustes(X,Y) returns the squared Procrustes Distance between the shapes of X and Y, which are represented by configurations of landmark points.

d = procrustes(X,Y,Name,Value) specifies additional options using one or more name-value arguments. For example, you can restrict the Procrustes transformation by disabling reflection and scaling.

[d,Z] = procrustes(___) also returns Z, the shape resulting from performing the Procrustes transformation on Y, using any of the input argument combinations in the previous syntaxes

[d,Z,transform] = procrustes(___) also returns the Procrustes transformation.

Examples

Find Procrustes Distance and Plot Superimposed Shape

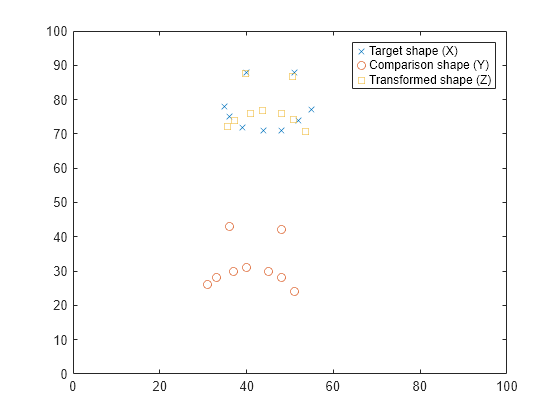
Construct matrices containing landmark points for two shapes, and visualize the shapes by plotting their landmark points.

X = [40 88; 51 88; 35 78; 36 75; 39 72; 44 71; 48 71; 52 74; 55 77];
Y = [36 43; 48 42; 31 26; 33 28; 37 30; 40 31; 45 30; 48 28; 51 24];
plot(X(:,1),X(:,2),"x")
hold on
plot(Y(:,1),Y(:,2),"o")
xlim([0 100])
ylim([0 100])
legend("Target shape (X)","Comparison shape (Y)")

Compare the shapes and view their Procrustes distance.

[d,Z] = procrustes(X,Y)

d = 
0.2026

Z = 9×2

   39.7694   87.5089
   50.5616   86.8011
   35.5487   72.1631
   37.3131   73.9909
   40.8735   75.8503
   43.5517   76.7959
   48.0577   75.9771
   50.7835   74.2286
   53.5410   70.6841

Visualize the shape that results from superimposing Y onto X.

plot(Z(:,1),Z(:,2),"s")
legend("Target shape (X)","Comparison shape (Y)", ...
    "Transformed shape (Z)")
hold off

Analyze Procrustes Transformation Including Rotation

Use the Procrustes transformation returned by procrustes to analyze how it superimposes the comparison shape onto the target shape.

Generate sample data in two dimensions.

rng("default")
n = 10;  
Y = normrnd(0,1,[n 2]);

Create the target shape X by rotating Y 60 degrees (pi/3 in radians), scaling the size of Y by factor 0.5, and then translating the points by adding 2. Also, add some noise to the landmark points in X.

S = [cos(pi/3) -sin(pi/3); sin(pi/3) cos(pi/3)]

S = 2×2

    0.5000   -0.8660
    0.8660    0.5000

X = normrnd(0.5*Y*S+2,0.05,n,2);

Find the Procrustes transformation that can transform Y to X.

[~,Z,transform] = procrustes(X,Y);

Display the components of the Procrustes transformation.

transform

transform = struct with fields:
    T: [2x2 double]
    b: 0.4845
    c: [10x2 double]

transform.T

ans = 2×2

    0.4832   -0.8755
    0.8755    0.4832

transform.c

ans = 10×2

    2.0325    1.9836
    2.0325    1.9836
    2.0325    1.9836
    2.0325    1.9836
    2.0325    1.9836
    2.0325    1.9836
    2.0325    1.9836
    2.0325    1.9836
    2.0325    1.9836
    2.0325    1.9836

transform.T is similar to the matrix S. Also, the scale component (transform.b) is close to 0.5, and the translation component values (transform.c) are close to 2.

Determine whether transform.T indicates a rotation or reflection by computing the determinant of transform.T. The determinant of a rotation matrix is 1, and the determinant of a reflection matrix is –1.

det(transform.T) 

ans = 
1

In two-dimensional space, a rotation matrix that rotates a point by an angle of $\theta$ degrees about the origin has the form

$\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]$.

If you use either $$\cos \theta$$ or $$\sin \theta$$, the rotation angle has two possible values between –180 and 180. Use both the $$\cos \theta$$ and $$\sin \theta$$ values to determine the rotation angle of the matrix without ambiguity. Using the atan2d function, you can determine the $$\tan \theta$$ value from $$\cos \theta$$ and $$\sin \theta$$, and also determine the angle.

theta = atan2d(transform.T(2,1),transform.T(1,1))

theta = 
61.1037

transform.T is a rotation matrix of 61 degrees.

Analyze Procrustes Transformation Including Reflection

Use the Procrustes transformation returned by procrustes to analyze how it superimposes the comparison shape onto the target shape.

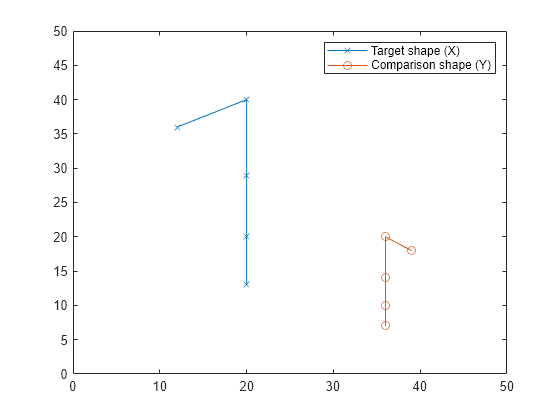
Create matrices with landmark points for two separate shapes.

X = [20 13; 20 20; 20, 29; 20 40; 12 36];
Y = [36 7; 36 10; 36 14; 36 20; 39 18];

Plot the landmark points to visualize the shapes.

plot(X(:,1),X(:,2),"-x")
hold on
plot(Y(:,1),Y(:,2),"-o")
xlim([0 50])
ylim([0 50])
legend("Target shape (X)","Comparison shape (Y)")
hold off

Obtain the Procrustes transformation by using procrustes.

[d,Z,transform] = procrustes(X,Y)

d = 
0.0064

Z = 5×2

   20.1177   13.3935
   19.9145   19.6790
   19.6435   28.0597
   19.2371   40.6306
   13.0871   36.2371

transform = struct with fields:
    T: [2x2 double]
    b: 2.0963
    c: [5x2 double]

transform.T

ans = 2×2

   -0.9995   -0.0323
   -0.0323    0.9995

transform.c

ans = 5×2

   96.0177    1.1661
   96.0177    1.1661
   96.0177    1.1661
   96.0177    1.1661
   96.0177    1.1661

The scale component of the transformation b indicates that the scale of X is about twice the scale of Y.

Find the determinant of the rotation and reflection component of the transformation.

det(transform.T)

ans = 
-1.0000

The determinant is –1, which means that the transformation contains a reflection.

In two-dimensional space, a reflection matrix has the form

$\left[\begin{array}{cc}\mathrm{cos2}\theta & \mathrm{sin2}\theta \\ \mathrm{sin2}\theta & -\mathrm{cos2}\theta \end{array}\right]$,

which indicates a reflection over a line that makes an angle $$\theta$$ with the x-axis.

If you use either $$\cos 2\theta$$ or $$\sin 2\theta$$, the angle for the line of reflection has two possible values between –90 and 90. Use both the $$\cos 2\theta$$ and $$\sin 2\theta$$ values to determine the angle for the line of reflection without ambiguity. Using the atan2d function, you can determine the $$\tan 2\theta$$ value from $$\cos 2\theta$$ and $$\sin 2\theta$$, and also determine the angle.

theta = atan2d(transform.T(2,1),transform.T(1,1))/2

theta = 
-89.0741

transform.T reflects points across a line that makes roughly a –90 degree angle with the x-axis; this line indicates the y-axis. The plots of X and Y show that reflecting across the y-axis is required to superimpose Y onto X.

Apply Procrustes Transformation to Larger Set of Points

Find the Procrustes transformation for landmark points, and apply the transformation to more points on the comparison shape than just the landmark points.

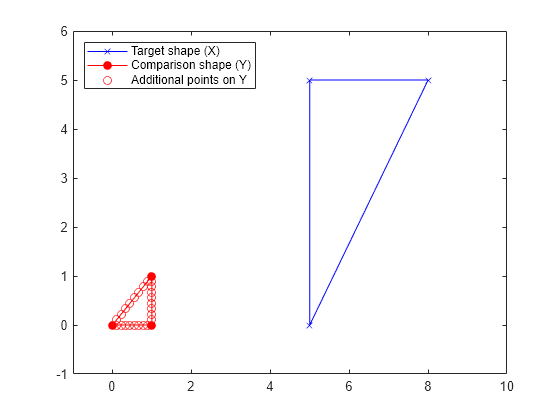
Create matrices with landmark points for two triangles X (target shape) and Y (comparison shape).

X = [5 0; 5 5; 8 5];
Y = [0 0; 1 0; 1 1];

Create a matrix with more points on the triangle Y.

Y_points = [linspace(Y(1,1),Y(2,1),10)' linspace(Y(1,2),Y(2,2),10)'
            linspace(Y(2,1),Y(3,1),10)' linspace(Y(2,2),Y(3,2),10)'
            linspace(Y(3,1),Y(1,1),10)' linspace(Y(3,2),Y(1,2),10)'];

Plot both shapes, including the larger set of points for the comparison shape.

plot([X(:,1); X(1,1)],[X(:,2); X(1,2)],"bx-")
hold on
plot([Y(:,1); Y(1,1)],[Y(:,2); Y(1,2)],"ro-","MarkerFaceColor","r")
plot(Y_points(:,1),Y_points(:,2),"ro")
xlim([-1 10])
ylim([-1 6])
legend("Target shape (X)","Comparison shape (Y)", ...
    "Additional points on Y","Location","northwest")

Call procrustes to obtain the Procrustes transformation from the comparison shape to the target shape.

[d,Z,transform] = procrustes(X,Y)

d = 
0.0441

Z = 3×2

    5.0000    0.5000
    4.5000    4.5000
    8.5000    5.0000

transform = struct with fields:
    T: [2x2 double]
    b: 4.0311
    c: [3x2 double]

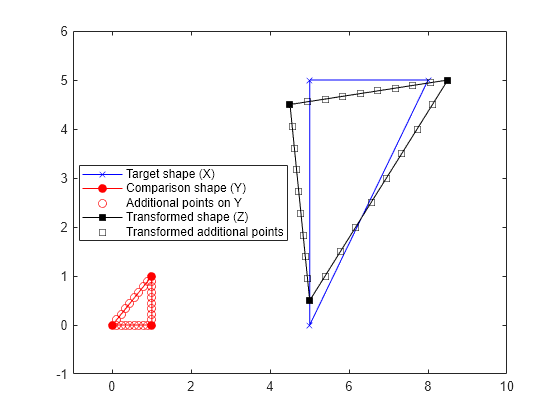
Use the Procrustes transformation to superimpose the other points (Y_points) on the comparison shape onto the target shape, and then visualize the results.

Z_points = transform.b*Y_points*transform.T + transform.c(1,:);
plot([Z(:,1); Z(1,1)],[Z(:,2); Z(1,2)],"ks-","MarkerFaceColor","k")
plot(Z_points(:,1),Z_points(:,2),"ks")
legend("Target shape (X)","Comparison shape (Y)", ...
    "Additional points on Y","Transformed shape (Z)", ...
    "Transformed additional points","Location","best")
hold off

Compare Shapes Without Reflection

Construct the shapes of the handwritten letters d and b using landmark points, and then plot the points to visualize the letters.

D = [33 93; 33 87; 33 80; 31 72; 32 65; 32 58; 30 72;
     28 72; 25 69; 22 64; 23 59; 26 57; 30 57];
B = [48 83; 48 77; 48 70; 48 65; 49 59; 49 56; 50 66;
     52 66; 56 65; 58 61; 57 57; 54 56; 51 55];
plot(D(:,1),D(:,2),"x-")
hold on
plot(B(:,1),B(:,2),"o-")
legend("Target shape (d)","Comparison shape (b)")
hold off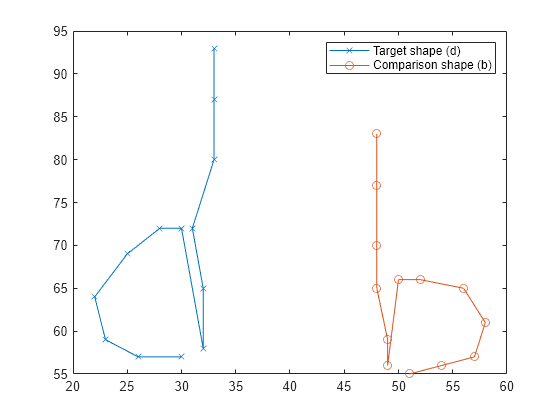

Use procrustes to compare the letters with reflection turned off, because reflection would turn the b into a d and not accurately preserve the shape you want to compare.

d = procrustes(D,B,"reflection",false)

d = 
0.3425

Try using procrustes with reflection on to see how the Procrustes distance differs.

d = procrustes(D,B,"reflection","best")

d = 
0.0204

This reflection setting results in a smaller Procrustes distance because reflecting b better aligns it with d.

Compare Shapes Without Scaling

Construct two shapes represented by their landmark points, and then plot the points to visualize them.

X = [20 13; 20 20; 20 29; 20 40; 12 36];
Y = [36  7; 36 10; 36 14; 36 20; 39 18];
plot(X(:,1),X(:,2),"-x")
hold on
plot(Y(:,1),Y(:,2),"-o")
xlim([0 50])
ylim([0 50])
legend("Target shape (X)","Comparison shape (Y)")

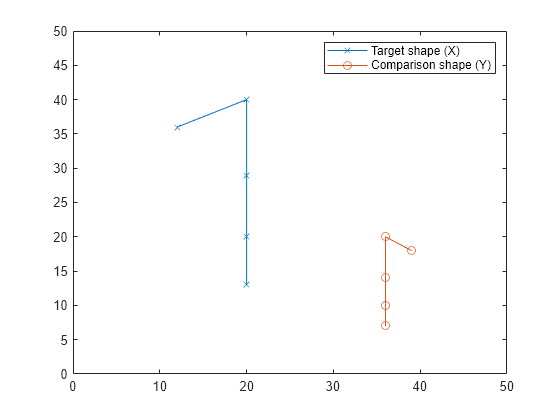
Compare the two shapes using Procrustes analysis with scaling turned off.

[d,Z] = procrustes(X,Y,"scaling",false)

d = 
0.2781

Z = 5×2

   19.2194   20.8229
   19.1225   23.8214
   18.9932   27.8193
   18.7993   33.8162
   15.8655   31.7202

Visualize the superimposed landmark points.

plot(Z(:,1),Z(:,2),"-s")
legend("Target shape (X)","Comparison shape (Y)", ...
    "Transformed shape (Z)")
hold off

The superimposed shape Z does not differ in scale from the original shape Y.

Input Arguments

X — Target shape

matrix

Target shape, specified as an n-by-p matrix where each of the n rows contains a p-dimensional landmark point. The landmark points represent the shape that is the target of the comparison.

Data Types: single | double

Y — Comparison shape

matrix

Comparison shape, specified as an n-by-q matrix where each of the n rows contains a q-dimensional landmark point with q ≤ p. The landmark points represent the shape to be compared with the target shape.

Y must have the same number of points (rows) as X, where each point in Y, Y(i,:) corresponds to the point in the same row in X, X(i,:).

Points in Y can have fewer dimensions (number of columns) than points in X. In this case, procrustes appends columns of zeros to Y to match the dimensions of X.

Data Types: single | double

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: d = procrustes(X,Y,"Scaling",false,"reflection",false) performs Procrustes analysis without scaling or reflection in the transformation.

Scaling — Flag to enable scaling

true or 1 (default) | false or 0

Flag to enable scaling in the Procrustes transformation, specified as logical 1 (true) or 0 (false). A value of false prevents scaling in the transformation. A value of true allows scaling if it minimizes the differences between the landmark points in X and Y.

Set Scaling to false to compare Y to X without scaling Y to match the scale of X. This option causes shapes of different scales to have a greater Procrustes distance.

Example: "Scaling",false

Data Types: logical

Reflection — Flag to enable reflection

"best" (default) | true or 1 | false or 0

Flag to enable reflection in the Procrustes transformation, specified as "best", logical 1 (true), or logical 0 (false).

• "best" — Find the optimal Procrustes transformation, regardless of whether or not it contains a reflection.

• 1 (true) — Force the Procrustes transformation to reflect Y, whether or not the transformation minimizes the differences between the landmark points.

• 0 (false) — Prevent the Procrustes transformation from reflecting Y. This option does not prevent rotation in the transformation.

Set Reflection to false to compare Y to X without reflecting Y to match the shape of X. This option causes shapes that are reflections of each other to have a greater Procrustes distance.

Example: "Reflection",true

Data Types: logical | string | char

Output Arguments

d — squared Procrustes distance

numeric scalar in the range [0,1]

Squared Procrustes distance, a measure of dissimilarity between two shapes, returned as a numeric scalar in the range [0,1]. If Scaling is set to false, the squared Procrustes distance can be outside of the range [0,1].

procrustes computes the distance using the sum of squared differences between the corresponding points in X and Z. The function then standardizes the distance by the scale of X. The scale of X is sum(sum((X-mean(X)).^2)), which is the sum of squared elements of a centered version of X where the columns of X have mean 0.

Data Types: single | double

Z — Transformed shape

numeric matrix

Transformed shape of the landmark points in Y, returned as an n-by-p numeric matrix that is the same size as X. The output Z is the result of applying the Procrustes transformation to Y.

Data Types: single | double

transform — Procrustes transformation

structure

Procrustes transformation, returned as a structure with three fields:

• T — Rotation and reflection component, specified by a p-by-p transformation matrix that rotates or reflects Y to match the orientation of the landmark points in X.

  • If T is a rotation matrix, then det(T) is 1.

  • If T is a reflection matrix, then det(T) is –1.

• b — Scale component, specified by a scalar to stretch (b > 1), conserve (b = 1), or shrink (b < 1) the scale of Y to match the scale of X.

• c — Translation component, specified by an n-by-p matrix where each row is the p-dimensional vector to add to the points in Y to shift it onto X.

The Procrustes transformation superimposes Y onto X by performing the following transformation:

Z = bYT + c.

Set the Reflection name-value argument to false to ensure that transform.T does not contain a reflection.

Set the Scaling name-value argument to false to remove the scale component, fixing transform.b to 1.

Data Types: struct

More About

Procrustes Distance

The Procrustes distance is a measure of dissimilarity between shapes based on Procrustes analysis.

The procrustes function finds the Procrustes transformation, which is the best shape-preserving Euclidean transformation (consisting of rotation, reflection, scaling, and translation) between the two shapes X and Y. The Procrustes transformation is an optimal transformation that minimizes the sum of squared differences between the landmark points in X and Z, where Z is the transformed shape of Y that results from superimposing Y onto X.

The procrustes function returns the squared Procrustes distance (d), transformed shape (Z), and Procrustes transformation (transform). The squared Procrustes distance is the sum of squared differences between X and Z.

Tips

• Procrustes analysis is appropriate when all dimensions in X and Y have similar scales. If the columns of X and Y have different scales, standardize the columns by using zscore or normalize.

• Procrustes analysis is useful in conjunction with multidimensional scaling. Two different applications of multidimensional scaling can produce reconstructed points that are similar in principle, but look different because they have different orientations. Also, the reconstructed points can have a different orientation than the original points. The procrustes function transforms one set of points to make them more comparable to the other. For an example, see Classical Multidimensional Scaling Applied to Nonspatial Distances.

References

[1] Kendall, David G. “A Survey of the Statistical Theory of Shape.” Statistical Science. Vol. 4, No. 2, 1989, pp. 87–99.

[2] Bookstein, Fred L. Morphometric Tools for Landmark Data. Cambridge, UK: Cambridge University Press, 1991.

[3] Seber, G. A. F. Multivariate Observations. Hoboken, NJ: John Wiley & Sons, Inc., 1984.

Version History

Introduced before R2006a