fit
Fit simple model of local interpretable model-agnostic explanations (LIME)
Syntax
Description
newresults = fit(results,queryPoint,numImportantPredictors)queryPoint) by
using the specified number of important predictors
(numImportantPredictors). The function returns a lime object
newresults that contains the new simple model.
fit uses the simple model options that you specify when you create
the lime object results. You can change the options
using the name-value pair arguments of the fit function.
newresults = fit(results,queryPoint,numImportantPredictors,Name,Value)'SimpleModelType','tree' to fit a decision tree model.
Examples
Train a regression model and create a lime object that uses a linear simple model. When you create a lime object, if you do not specify a query point and the number of important predictors, then the software generates samples of a synthetic data set but does not fit a simple model. Use the object function fit to fit a simple model for a query point. Then display the coefficients of the fitted linear simple model by using the object function plot.
Load the carbig data set, which contains measurements of cars made in the 1970s and early 1980s.
load carbigCreate a table containing the predictor variables Acceleration, Cylinders, and so on, as well as the response variable MPG.
tbl = table(Acceleration,Cylinders,Displacement,Horsepower,Model_Year,Weight,MPG);
Removing missing values in a training set can help reduce memory consumption and speed up training for the fitrkernel function. Remove missing values in tbl.
tbl = rmmissing(tbl);
Create a table of predictor variables by removing the response variable from tbl.
tblX = removevars(tbl,'MPG');Train a blackbox model of MPG by using the fitrkernel function.
rng('default') % For reproducibility mdl = fitrkernel(tblX,tbl.MPG,'CategoricalPredictors',[2 5]);
Create a lime object. Specify a predictor data set because mdl does not contain predictor data.
results = lime(mdl,tblX)
results =
lime with properties:
BlackboxModel: [1×1 RegressionKernel]
DataLocality: 'global'
CategoricalPredictors: [2 5]
Type: 'regression'
X: [392×6 table]
QueryPoint: []
NumImportantPredictors: []
NumSyntheticData: 5000
SyntheticData: [5000×6 table]
Fitted: [5000×1 double]
SimpleModel: []
ImportantPredictors: []
BlackboxFitted: []
SimpleModelFitted: []
results contains the generated synthetic data set. The SimpleModel property is empty ([]).
Fit a linear simple model for the first observation in tblX. Specify the number of important predictors to find as 3.
queryPoint = tblX(1,:)
queryPoint=1×6 table
Acceleration Cylinders Displacement Horsepower Model_Year Weight
____________ _________ ____________ __________ __________ ______
12 8 307 130 70 3504
results = fit(results,queryPoint,3);
Plot the lime object results by using the object function plot.
plot(results)

The plot displays two predictions for the query point, which correspond to the BlackboxFitted property and the SimpleModelFitted property of results.
The horizontal bar graph shows the coefficient values of the simple model, sorted by their absolute values. LIME finds Horsepower, Model_Year, and Cylinders as important predictors for the query point.
Model_Year and Cylinders are categorical predictors that have multiple categories. For a linear simple model, the software creates one less dummy variable than the number of categories for each categorical predictor. The bar graph displays only the most important dummy variable. You can check the coefficients of the other dummy variables using the SimpleModel property of results. Display the sorted coefficient values, including all categorical dummy variables.
[~,I] = sort(abs(results.SimpleModel.Beta),'descend'); table(results.SimpleModel.ExpandedPredictorNames(I)',results.SimpleModel.Beta(I), ... 'VariableNames',{'Expanded Predictor Name','Coefficient'})
ans=17×2 table
Expanded Predictor Name Coefficient
__________________________ ___________
{'Horsepower' } -3.5035e-05
{'Model_Year (74 vs. 70)'} -6.1591e-07
{'Model_Year (80 vs. 70)'} -3.9803e-07
{'Model_Year (81 vs. 70)'} 3.4186e-07
{'Model_Year (82 vs. 70)'} -2.2331e-07
{'Cylinders (6 vs. 8)' } -1.9807e-07
{'Model_Year (76 vs. 70)'} 1.816e-07
{'Cylinders (5 vs. 8)' } 1.7318e-07
{'Model_Year (71 vs. 70)'} 1.5694e-07
{'Model_Year (75 vs. 70)'} 1.5486e-07
{'Model_Year (77 vs. 70)'} 1.5151e-07
{'Model_Year (78 vs. 70)'} 1.3864e-07
{'Model_Year (72 vs. 70)'} 6.8949e-08
{'Cylinders (4 vs. 8)' } 6.3098e-08
{'Model_Year (73 vs. 70)'} 4.9696e-08
{'Model_Year (79 vs. 70)'} -2.4822e-08
⋮
Train a classification model and create a lime object that uses a decision tree simple model. Fit multiple models for multiple query points.
Load the CreditRating_Historical data set. The data set contains customer IDs and their financial ratios, industry labels, and credit ratings.
tbl = readtable('CreditRating_Historical.dat');Create a table of predictor variables by removing the columns of customer IDs and ratings from tbl.
tblX = removevars(tbl,["ID","Rating"]);
Train a blackbox model of credit ratings by using the fitcecoc function.
blackbox = fitcecoc(tblX,tbl.Rating,'CategoricalPredictors','Industry')
blackbox =
ClassificationECOC
PredictorNames: {'WC_TA' 'RE_TA' 'EBIT_TA' 'MVE_BVTD' 'S_TA' 'Industry'}
ResponseName: 'Y'
CategoricalPredictors: 6
ClassNames: {'A' 'AA' 'AAA' 'B' 'BB' 'BBB' 'CCC'}
ScoreTransform: 'none'
BinaryLearners: {21×1 cell}
CodingName: 'onevsone'
Properties, Methods
Create a lime object with the blackbox model.
rng('default') % For reproducibility results = lime(blackbox);
Find two query points whose true rating values are AAA and B, respectively.
queryPoint(1,:) = tblX(find(strcmp(tbl.Rating,'AAA'),1),:); queryPoint(2,:) = tblX(find(strcmp(tbl.Rating,'B'),1),:)
queryPoint=2×6 table
WC_TA RE_TA EBIT_TA MVE_BVTD S_TA Industry
_____ _____ _______ ________ _____ ________
0.121 0.413 0.057 3.647 0.466 12
0.019 0.009 0.042 0.257 0.119 1
Fit a linear simple model for the first query point. Set the number of important predictors to 4.
newresults1 = fit(results,queryPoint(1,:),4);
Plot the LIME results newresults1 for the first query point.
plot(newresults1)
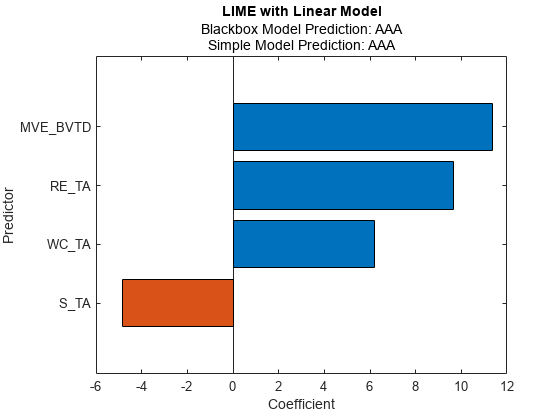
Fit a linear decision tree model for the first query point.
newresults2 = fit(results,queryPoint(1,:),6,'SimpleModelType','tree'); plot(newresults2)

The simple models in newresults1 and newresults2 both find MVE_BVTD and RE_TA as important predictors.
Fit a linear simple model for the second query point, and plot the LIME results for the second query point.
newresults3 = fit(results,queryPoint(2,:),4); plot(newresults3)
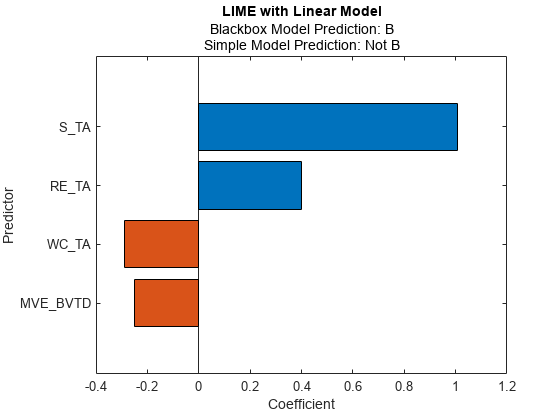
The prediction from the blackbox model is B, but the prediction from the simple model is not B. When the two predictions are not the same, you can specify a smaller 'KernelWidth' value. The software fits a simple model using weights that are more focused on the samples near the query point. If a query point is an outlier or is located near a decision boundary, then the two prediction values can be different, even if you specify a small 'KernelWidth' value. In such a case, you can change other name-value pair arguments. For example, you can generate a local synthetic data set (specify 'DataLocality' of lime as 'local') for the query point and increase the number of samples ('NumSyntheticData' of lime or fit) in the synthetic data set. You can also use a different distance metric ('Distance' of lime or fit).
Fit a linear simple model with a small 'KernelWidth' value.
newresults4 = fit(results,queryPoint(2,:),4,'KernelWidth',0.01);
plot(newresults4)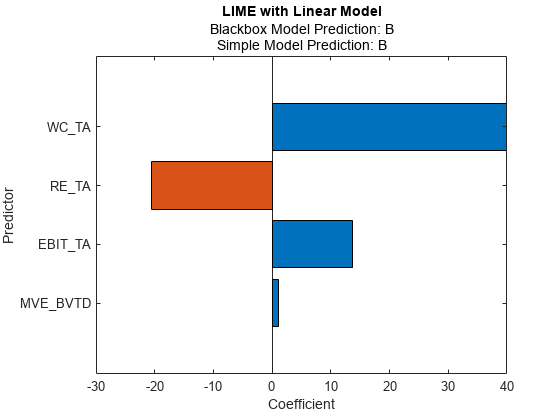
The credit ratings for the first and second query points are AAA and B, respectively. The simple models in newresults1 and newresults4 both find MVE_BVTD, RE_TA, and WC_TA as important predictors. However, their coefficient values are different. The plots show that these predictors act differently depending on the credit ratings.
Input Arguments
LIME results, specified as a lime
object.
Query point around which the fit function fits the simple
model, specified as a row vector of numeric values or a single-row table. The
queryPoint value must have the same data type and the same number
of columns as the predictor data (results.
or Xresults.) in the SyntheticDatalime object
results.
queryPoint must not contain missing values.
Data Types: single | double | table
Number of important predictors to use in the simple model, specified as a positive integer scalar value.
If
'SimpleModelType'is'linear', then the software selects the specified number of important predictors and fits a linear model of the selected predictors. Note that the software does not use unimportant predictors when fitting the linear model.If
'SimpleModelType'is'tree', then the software specifies the maximum number of decision splits (or branch nodes) as the number of important predictors so that the fitted decision tree uses at most the specified number of predictors.
The default value of the numImportantPredictors argument is the
NumImportantPredictors property value of the lime object
results. If you do not specify the property value when creating
results, then the property value is empty ([])
and you must specify this argument.
Data Types: single | double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: 'NumSyntheticData',2000,'SimpleModelType','tree' sets the
number of samples to generate for the synthetic data set to 2000 and specifies the simple
model type as a decision tree.
Since R2023b
Relative tolerance on the linear coefficients and the bias term (intercept) for the linear simple model, specified as a nonnegative scalar.
This argument is valid only when the SimpleModelType value is
"linear".
Let , that is, the vector of the coefficients and the bias term at fitting step t. If , then the fitting process for the linear simple model terminates.
Example: "BetaTolerance",1e-8
Data Types: single | double
Covariance matrix for the Mahalanobis distance metric, specified as the
comma-separated pair consisting of 'Cov' and a
K-by-K positive definite matrix, where
K is the number of predictors.
This argument is valid only if 'Distance' is
'mahalanobis'.
The default value is the 'Cov' value that you specify when
creating the lime object results. The default
'Cov' value of lime is
cov(PD,'omitrows'), where PD is the predictor
data or synthetic predictor data. If you do not specify the 'Cov'
value, then the software uses different covariance matrices when computing the
distances for both the predictor data and the synthetic predictor data.
Example: 'Cov',eye(3)
Data Types: single | double
Distance metric, specified as the comma-separated pair consisting of 'Distance' and a character vector, string scalar, or function handle.
If the predictor data includes only continuous variables, then
fitsupports these distance metrics.Value Description 'euclidean'Euclidean distance.
'seuclidean'Standardized Euclidean distance. Each coordinate difference between observations is scaled by dividing by the corresponding element of the standard deviation,
S = std(PD,'omitnan'), wherePDis the predictor data or synthetic predictor data. To specify different scaling, use the'Scale'name-value argument.'mahalanobis'Mahalanobis distance using the sample covariance of
PD,C = cov(PD,'omitrows'). To change the value of the covariance matrix, use the'Cov'name-value argument.'cityblock'City block distance.
'minkowski'Minkowski distance. The default exponent is 2. To specify a different exponent, use the
'P'name-value argument.'chebychev'Chebychev distance (maximum coordinate difference).
'cosine'One minus the cosine of the included angle between points (treated as vectors).
'correlation'One minus the sample correlation between points (treated as sequences of values).
'spearman'One minus the sample Spearman's rank correlation between observations (treated as sequences of values).
@distfunCustom distance function handle. A distance function has the form
wherefunction D2 = distfun(ZI,ZJ) % calculation of distance ...
ZIis a1-by-tvector containing a single observation.ZJis ans-by-tmatrix containing multiple observations.distfunmust accept a matrixZJwith an arbitrary number of observations.D2is ans-by-1vector of distances, andD2(k)is the distance between observationsZIandZJ(k,:).
If your data is not sparse, you can generally compute distance more quickly by using a built-in distance metric instead of a function handle.
If the predictor data includes both continuous and categorical variables, then
fitsupports these distance metrics.Value Description 'goodall3'Modified Goodall distance
'ofd'Occurrence frequency distance
For definitions, see Distance Metrics.
The default value is the 'Distance' value that you specify when
creating the lime object results. The default
'Distance' value of lime is
'euclidean' if the predictor data includes only continuous
variables, or 'goodall3' if the predictor data includes both
continuous and categorical variables.
Example: 'Distance','ofd'
Data Types: char | string | function_handle
Kernel width of the squared exponential (or Gaussian) kernel function, specified as the comma-separated pair consisting of 'KernelWidth' and a numeric scalar value.
The fit function computes distances between the query point and
the samples in the synthetic predictor data set, and then converts the distances to weights
by using the squared exponential kernel function. If you lower the
'KernelWidth' value, then fit uses
weights that are more focused on the samples near the query point. For details, see LIME.
The default value is the 'KernelWidth' value that you specify
when creating the lime object results. The
default 'KernelWidth' value of lime is
0.75.
Example: 'KernelWidth',0.5
Data Types: single | double
Number of neighbors of the query point, specified as the comma-separated pair
consisting of 'NumNeighbors' and a positive integer scalar value.
This argument is valid only when the DataLocality property of results is
'local'.
The fit function estimates the distribution
parameters of the predictor data using the specified number of nearest neighbors of
the query point. Then the function generates synthetic predictor data using the
estimated distribution.
If you specify a value larger than the number of observations in the predictor
data set (results.) in the Xlime object
results, then fit uses all
observations.
The default value is the 'NumNeighbors' value that you specify
when creating the lime object results. The
default 'NumNeighbors' value of lime is
1500.
Example: 'NumNeighbors',2000
Data Types: single | double
Number of samples to generate for the synthetic data set, specified as the
comma-separated pair consisting of 'NumSyntheticData' and a
positive integer scalar value.
The default value is the NumSyntheticData property value of the lime object
results. If you provide a custom synthetic data set when
creating results, then the property value is the number of
samples in the data set. Otherwise, the 'NumSyntheticData' value
that you specify when creating results sets the property. The
default 'NumSyntheticData' value of lime is
5000.
Example: 'NumSyntheticData',2500
Data Types: single | double
Exponent for the Minkowski distance metric, specified as the comma-separated pair
consisting of 'P' and a positive scalar.
This argument is valid only if 'Distance' is
'minkowski'.
The default value is the 'P' value that you specify when
creating the lime object results. The default
'P' value of lime is 2.
Example: 'P',3
Data Types: single | double
Scale parameter value for the standardized Euclidean distance metric, specified as
the comma-separated pair consisting of 'Scale' and a nonnegative
numeric vector of length K, where K is the
number of predictors.
This argument is valid only if 'Distance' is
'seuclidean'.
The default value is the 'Scale' value that you specify when
creating the lime object results. The default
'Scale' value of lime is
std(PD,'omitnan'), where PD is the predictor
data or synthetic predictor data. If you do not specify the
'Scale' value, then the software uses different scale
parameters when computing the distances for both the predictor data and the synthetic
predictor data.
Example: 'Scale',quantile(X,0.75) -
quantile(X,0.25)
Data Types: single | double
Type of the simple model, specified as the comma-separated pair consisting of 'SimpleModelType' and 'linear' or 'tree'.
'linear'— The software fits a linear model by usingfitrlinearfor regression orfitclinearfor classification.'tree'— The software fits a decision tree model by usingfitrtreefor regression orfitctreefor classification.
The default value is the 'SimpleModelType' value that you
specify when creating the lime object results.
The default 'SimpleModelType' value of lime is
'linear'.
Example: 'SimpleModelType','tree'
Data Types: char | string
Output Arguments
More About
A distance metric is a function that defines a distance between two
observations. fit supports various distance metrics for
continuous variables and a mix of continuous and categorical variables.
Distance metrics for continuous variables
Given an mx-by-n data matrix X, which is treated as mx (1-by-n) row vectors x1, x2, ..., xmx, and an my-by-n data matrix Y, which is treated as my (1-by-n) row vectors y1, y2, ...,ymy, the various distances between the vector xs and yt are defined as follows:
Euclidean distance
The Euclidean distance is a special case of the Minkowski distance, where p = 2.
Standardized Euclidean distance
where V is the n-by-n diagonal matrix whose jth diagonal element is (S(j))2, where S is a vector of scaling factors for each dimension.
Mahalanobis distance
where C is the covariance matrix.
City block distance
The city block distance is a special case of the Minkowski distance, where p = 1.
Minkowski distance
For the special case of p = 1, the Minkowski distance gives the city block distance. For the special case of p = 2, the Minkowski distance gives the Euclidean distance. For the special case of p = ∞, the Minkowski distance gives the Chebychev distance.
Chebychev distance
The Chebychev distance is a special case of the Minkowski distance, where p = ∞.
Cosine distance
Correlation distance
where
and
Spearman distance is one minus the sample Spearman's rank correlation between observations (treated as sequences of values):
where
Distance metrics for a mix of continuous and categorical variables
Modified Goodall distance
This distance is a variant of the Goodall distance, which assigns a small distance if the matching values are infrequent regardless of the frequencies of the other values. For mismatches, the distance contribution of the predictor is 1/(number of variables).
Occurrence frequency distance
For a match, the occurrence frequency distance assigns zero distance. For a mismatch, the occurrence frequency distance assigns a higher distance on a less frequent value and a lower distance on a more frequent value.
Algorithms
To explain a prediction of a machine learning model using LIME [1], the software generates a synthetic data
set and fits a simple interpretable model to the synthetic data set by using
lime and fit, as described in steps
1–5.
If you specify the
queryPointandnumImportantPredictorsvalues oflime, then thelimefunction performs all steps.If you do not specify
queryPointandnumImportantPredictorsand specify'DataLocality'as'global'(default), then thelimefunction generates a synthetic data set (steps 1–2), and thefitfunction fits a simple model (steps 3–5).If you do not specify
queryPointandnumImportantPredictorsand specify'DataLocality'as'local', then thefitfunction performs all steps.
The lime and fit functions perform these
steps:
Generate a synthetic predictor data set Xs using a multivariate normal distribution for continuous variables and a multinomial distribution for each categorical variable. You can specify the number of samples to generate by using the
'NumSyntheticData'name-value argument.If
'DataLocality'is'global'(default), then the software estimates the distribution parameters from the whole predictor data set (Xor predictor data inblackbox).If
'DataLocality'is'local', then the software estimates the distribution parameters using the k-nearest neighbors of the query point, where k is the'NumNeighbors'value. You can specify a distance metric to find the nearest neighbors by using the'Distance'name-value argument.
The software ignores missing values in the predictor data set when estimating the distribution parameters.
Alternatively, you can provide a pregenerated, custom synthetic predictor data set by using the
customSyntheticDatainput argument oflime.Compute the predictions Ys for the synthetic data set Xs. The predictions are predicted responses for regression or classified labels for classification. The software uses the
predictfunction of theblackboxmodel to compute the predictions. If you specifyblackboxas a function handle, then the software computes the predictions by using the function handle.Compute the distances d between the query point and the samples in the synthetic predictor data set using the distance metric specified by
'Distance'.Compute the weight values wq of the samples in the synthetic predictor data set with respect to the query point q using the squared exponential (or Gaussian) kernel function
xs is a sample in the synthetic predictor data set Xs.
d(xs,q) is the distance between the sample xs and the query point q.
p is the number of predictors in Xs.
σ is the kernel width, which you can specify by using the
'KernelWidth'name-value argument. The default'KernelWidth'value is 0.75.
The weight value at the query point is 1, and then it converges to zero as the distance value increases. The
'KernelWidth'value controls how fast the weight value converges to zero. The lower the'KernelWidth'value, the faster the weight value converges to zero. Therefore, the algorithm gives more weight to samples near the query point. Because this algorithm uses such weight values, the selected important predictors and fitted simple model effectively explain the predictions for the synthetic data locally, around the query point.Fit a simple model.
If
'SimpleModelType'is'linear'(default), then the software selects important predictors and fits a linear model of the selected important predictors.Select n important predictors () by using the group orthogonal matching pursuit (OMP) algorithm [2][3], where n is the
numImportantPredictorsvalue. This algorithm uses the synthetic predictor data set (Xs), predictions (Ys), and weight values (wq).Note that the software does not select unimportant predictors (with estimated 0 coefficients), so the number of selected important predictors might be less than n.
Fit a linear model of the selected important predictors () to the predictions (Ys) using the weight values (wq). The software uses
fitrlinearfor regression orfitclinearfor classification. For a multiclass model, the software uses the one-versus-all scheme to construct a binary classification problem. The positive class is the predicted class for the query point from theblackboxmodel, and the negative class refers to the other classes.
If
'SimpleModelType'is'tree', then the software fits a decision tree model by usingfitrtreefor regression orfitctreefor classification. The software specifies the maximum number of decision splits (or branch nodes) as the number of important predictors so that the fitted decision tree uses at most the specified number of predictors.
References
[1] Ribeiro, Marco Tulio, S. Singh, and C. Guestrin. "'Why Should I Trust You?': Explaining the Predictions of Any Classifier." In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 1135–44. San Francisco, California: ACM, 2016.
[2] Świrszcz, Grzegorz, Naoki Abe, and Aurélie C. Lozano. "Grouped Orthogonal Matching Pursuit for Variable Selection and Prediction." Advances in Neural Information Processing Systems (2009): 1150–58.
[3] Lozano, Aurélie C., Grzegorz Świrszcz, and Naoki Abe. "Group Orthogonal Matching Pursuit for Logistic Regression." Proceedings of the Fourteenth International Conference on Artificial Intelligence and Statistics (2011): 452–60.
Version History
Introduced in R2020bIf you compute LIME values by fitting a linear simple model (see
SimpleModelType), you can specify the relative tolerance on the
linear coefficients and the bias term of the simple model by using the
BetaTolerance name-value argument. The default
BetaTolerance value is 1e-4.
In R2023a, the relative tolerance on the linear coefficients of the linear simple model
was 1e-8. In previous releases, the value was
1e-4.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)