kmeans
k-means clustering
Syntax
Description
idx = kmeans(X,k)X
into k clusters, and returns an n-by-1 vector
(idx) containing cluster indices of each observation. Rows of
X correspond to points and columns correspond to variables.
By default, kmeans uses the squared Euclidean distance metric and the k-means++
algorithm for cluster center initialization.
idx = kmeans(X,k,Name,Value)Name,Value pair
arguments.
For example, specify the cosine distance, the number of times to repeat the clustering using new initial values, or to use parallel computing.
Examples
Cluster data using k-means clustering, then plot the cluster regions.
Load Fisher's iris data set. Use the petal lengths and widths as predictors.
load fisheriris X = meas(:,3:4); figure; plot(X(:,1),X(:,2),'k*','MarkerSize',5); title 'Fisher''s Iris Data'; xlabel 'Petal Lengths (cm)'; ylabel 'Petal Widths (cm)';

The larger cluster seems to be split into a lower variance region and a higher variance region. This might indicate that the larger cluster is two, overlapping clusters.
Cluster the data. Specify k = 3 clusters.
rng(1); % For reproducibility
[idx,C] = kmeans(X,3);idx is a vector of predicted cluster indices corresponding to the observations in X. C is a 3-by-2 matrix containing the final centroid locations.
Use kmeans to compute the distance from each centroid to points on a grid. To do this, pass the centroids (C) and points on a grid to kmeans, and implement one iteration of the algorithm.
x1 = min(X(:,1)):0.01:max(X(:,1)); x2 = min(X(:,2)):0.01:max(X(:,2)); [x1G,x2G] = meshgrid(x1,x2); XGrid = [x1G(:),x2G(:)]; % Defines a fine grid on the plot idx2Region = kmeans(XGrid,3,'MaxIter',1,'Start',C);
Warning: Failed to converge in 1 iterations.
% Assigns each node in the grid to the closest centroidkmeans displays a warning stating that the algorithm did not converge, which you should expect since the software only implemented one iteration.
Plot the cluster regions.
figure; gscatter(XGrid(:,1),XGrid(:,2),idx2Region,... [0,0.75,0.75;0.75,0,0.75;0.75,0.75,0],'..'); hold on; plot(X(:,1),X(:,2),'k*','MarkerSize',5); title 'Fisher''s Iris Data'; xlabel 'Petal Lengths (cm)'; ylabel 'Petal Widths (cm)'; legend('Region 1','Region 2','Region 3','Data','Location','SouthEast'); hold off;

Randomly generate the sample data.
rng default; % For reproducibility X = [randn(100,2)*0.75+ones(100,2); randn(100,2)*0.5-ones(100,2)]; figure; plot(X(:,1),X(:,2),'.'); title 'Randomly Generated Data';

There appears to be two clusters in the data.
Partition the data into two clusters, and choose the best arrangement out of five initializations. Display the final output.
opts = statset('Display','final'); [idx,C] = kmeans(X,2,'Distance','cityblock',... 'Replicates',5,'Options',opts);
Replicate 1, 3 iterations, total sum of distances = 0.9879171.79822.012450.8117850.42111.476630.935910.7658763.92211.979431.424072.662641.514380.8970231.211160.4900031.413872.344710.9618081.725542.639011.767771.526541.773070.474890.737131.323370.48160.7009451.910930.6884431.523612.030061.231352.433221.058281.000911.655061.244741.553550.3370910.4231971.308820.2056411.31780.8025581.036580.6277072.078681.509511.281030.1702011.127751.479361.012391.006141.158761.246460.3833821.036551.082730.6571421.011252.674342.354170.4094451.978721.251440.9742022.310791.506322.065221.276750.8709761.110391.63371.212310.4582970.5357611.03681.842510.5143450.5416491.19871.261181.256171.22131.371520.6112451.066731.0530.1301640.525781.910790.7818770.722291.450342.043190.5321252.058140.1718340.948870.720610.5322740.5367080.5896830.3956460.534580.5077240.3546260.728470.8935010.4712120.7593141.377580.7991450.6911630.2880741.129630.5508960.9993251.023740.7261060.2204910.9175090.4357990.5026970.2129291.156380.8346460.4969721.187010.5606991.044620.2570.4003661.135382.097341.43670.8821421.192170.5808720.2976160.401890.214231.58420.2424841.005980.4217950.1035350.8210810.1905330.4947271.102361.129220.3802381.103781.424281.211780.6076250.7203680.8542731.048020.5291860.6439461.002930.3392271.094660.1616450.3560030.8847070.6776620.9006650.332320.3368890.8842620.7647690.6776980.9044340.5589671.708050.8172460.3194670.8796910.9693671.099070.8290530.732971.020470.979410.2533961.089880.7817340.9302050.4414340.1001132.052320.634641.114861.52274. Replicate 2, 5 iterations, total sum of distances = 0.9879171.79822.012450.8117850.42111.476630.935910.7658763.92211.979431.424072.662641.514380.8970231.211160.4900031.413872.344710.9618081.725542.639011.767771.526541.773070.474890.737131.323370.48160.7009451.910930.6884431.523612.030061.231352.433221.058281.000911.655061.244741.553550.3370910.4231971.308820.2056411.31780.8025581.036580.6277072.078681.509511.281030.1702011.127751.479361.012391.006141.158761.246460.3833821.036551.082730.6571421.011252.674342.354170.4094451.978721.251440.9742022.310791.506322.065221.276750.8709761.110391.63371.212310.4582970.5357611.03681.842510.5143450.5416491.19871.261181.256171.22131.371520.6112451.066731.0530.1301640.525781.910790.7818770.722291.450342.043190.5321252.058140.1718340.948870.720610.5322740.5367080.5896830.3956460.534580.5077240.3546260.728470.8935010.4712120.7593141.377580.7991450.6911630.2880741.129630.5508960.9993251.023740.7261060.2204910.9175090.4357990.5026970.2129291.156380.8346460.4969721.187010.5606991.044620.2570.4003661.135382.097341.43670.8821421.192170.5808720.2976160.401890.214231.58420.2424841.005980.4217950.1035350.8210810.1905330.4947271.102361.129220.3802381.103781.424281.211780.6076250.7203680.8542731.048020.5291860.6439461.002930.3392271.094660.1616450.3560030.8847070.6776620.9006650.332320.3368890.8842620.7647690.6776980.9044340.5589671.708050.8172460.3194670.8796910.9693671.099070.8290530.732971.020470.979410.2533961.089880.7817340.9302050.4414340.1001132.052320.634641.114861.52274. Replicate 3, 3 iterations, total sum of distances = 0.9879171.79822.012450.8117850.42111.476630.935910.7658763.92211.979431.424072.662641.514380.8970231.211160.4900031.413872.344710.9618081.725542.639011.767771.526541.773070.474890.737131.323370.48160.7009451.910930.6884431.523612.030061.231352.433221.058281.000911.655061.244741.553550.3370910.4231971.308820.2056411.31780.8025581.036580.6277072.078681.509511.281030.1702011.127751.479361.012391.006141.158761.246460.3833821.036551.082730.6571421.011252.674342.354170.4094451.978721.251440.9742022.310791.506322.065221.276750.8709761.110391.63371.212310.4582970.5357611.03681.842510.5143450.5416491.19871.261181.256171.22131.371520.6112451.066731.0530.1301640.525781.910790.7818770.722291.450342.043190.5321252.058140.1718340.948870.720610.5322740.5367080.5896830.3956460.534580.5077240.3546260.728470.8935010.4712120.7593141.377580.7991450.6911630.2880741.129630.5508960.9993251.023740.7261060.2204910.9175090.4357990.5026970.2129291.156380.8346460.4969721.187010.5606991.044620.2570.4003661.135382.097341.43670.8821421.192170.5808720.2976160.401890.214231.58420.2424841.005980.4217950.1035350.8210810.1905330.4947271.102361.129220.3802381.103781.424281.211780.6076250.7203680.8542731.048020.5291860.6439461.002930.3392271.094660.1616450.3560030.8847070.6776620.9006650.332320.3368890.8842620.7647690.6776980.9044340.5589671.708050.8172460.3194670.8796910.9693671.099070.8290530.732971.020470.979410.2533961.089880.7817340.9302050.4414340.1001132.052320.634641.114861.52274. Replicate 4, 3 iterations, total sum of distances = 0.9879171.79822.012450.8117850.42111.476630.935910.7658763.92211.979431.424072.662641.514380.8970231.211160.4900031.413872.344710.9618081.725542.639011.767771.526541.773070.474890.737131.323370.48160.7009451.910930.6884431.523612.030061.231352.433221.058281.000911.655061.244741.553550.3370910.4231971.308820.2056411.31780.8025581.036580.6277072.078681.509511.281030.1702011.127751.479361.012391.006141.158761.246460.3833821.036551.082730.6571421.011252.674342.354170.4094451.978721.251440.9742022.310791.506322.065221.276750.8709761.110391.63371.212310.4582970.5357611.03681.842510.5143450.5416491.19871.261181.256171.22131.371520.6112451.066731.0530.1301640.525781.910790.7818770.722291.450342.043190.5321252.058140.1718340.948870.720610.5322740.5367080.5896830.3956460.534580.5077240.3546260.728470.8935010.4712120.7593141.377580.7991450.6911630.2880741.129630.5508960.9993251.023740.7261060.2204910.9175090.4357990.5026970.2129291.156380.8346460.4969721.187010.5606991.044620.2570.4003661.135382.097341.43670.8821421.192170.5808720.2976160.401890.214231.58420.2424841.005980.4217950.1035350.8210810.1905330.4947271.102361.129220.3802381.103781.424281.211780.6076250.7203680.8542731.048020.5291860.6439461.002930.3392271.094660.1616450.3560030.8847070.6776620.9006650.332320.3368890.8842620.7647690.6776980.9044340.5589671.708050.8172460.3194670.8796910.9693671.099070.8290530.732971.020470.979410.2533961.089880.7817340.9302050.4414340.1001132.052320.634641.114861.52274. Replicate 5, 2 iterations, total sum of distances = 0.9879171.79822.012450.8117850.42111.476630.935910.7658763.92211.979431.424072.662641.514380.8970231.211160.4900031.413872.344710.9618081.725542.639011.767771.526541.773070.474890.737131.323370.48160.7009451.910930.6884431.523612.030061.231352.433221.058281.000911.655061.244741.553550.3370910.4231971.308820.2056411.31780.8025581.036580.6277072.078681.509511.281030.1702011.127751.479361.012391.006141.158761.246460.3833821.036551.082730.6571421.011252.674342.354170.4094451.978721.251440.9742022.310791.506322.065221.276750.8709761.110391.63371.212310.4582970.5357611.03681.842510.5143450.5416491.19871.261181.256171.22131.371520.6112451.066731.0530.1301640.525781.910790.7818770.722291.450342.043190.5321252.058140.1718340.948870.720610.5322740.5367080.5896830.3956460.534580.5077240.3546260.728470.8935010.4712120.7593141.377580.7991450.6911630.2880741.129630.5508960.9993251.023740.7261060.2204910.9175090.4357990.5026970.2129291.156380.8346460.4969721.187010.5606991.044620.2570.4003661.135382.097341.43670.8821421.192170.5808720.2976160.401890.214231.58420.2424841.005980.4217950.1035350.8210810.1905330.4947271.102361.129220.3802381.103781.424281.211780.6076250.7203680.8542731.048020.5291860.6439461.002930.3392271.094660.1616450.3560030.8847070.6776620.9006650.332320.3368890.8842620.7647690.6776980.9044340.5589671.708050.8172460.3194670.8796910.9693671.099070.8290530.732971.020470.979410.2533961.089880.7817340.9302050.4414340.1001132.052320.634641.114861.52274. Best total sum of distances = 201.533
By default, the software initializes the replicates separately using k-means++.
Plot the clusters and the cluster centroids.
figure; plot(X(idx==1,1),X(idx==1,2),'r.','MarkerSize',12) hold on plot(X(idx==2,1),X(idx==2,2),'b.','MarkerSize',12) plot(C(:,1),C(:,2),'kx',... 'MarkerSize',15,'LineWidth',3) legend('Cluster 1','Cluster 2','Centroids',... 'Location','NW') title 'Cluster Assignments and Centroids' hold off

You can determine how well separated the clusters are by passing idx to silhouette.
Clustering large data sets might take time, particularly if you use online updates (set by default). If you have a Parallel Computing Toolbox™ license and you set the options for parallel computing, then kmeans runs each clustering task (or replicate) in parallel. And, if Replicates>1, then parallel computing decreases time to convergence.
Randomly generate a large data set from a Gaussian mixture model.
rng(1); % For reproducibility Mu = ones(20,30).*(1:20)'; % Gaussian mixture mean rn30 = randn(30,30); Sigma = rn30'*rn30; % Symmetric and positive-definite covariance Mdl = gmdistribution(Mu,Sigma); % Define the Gaussian mixture distribution X = random(Mdl,10000);
Mdl is a 30-dimensional gmdistribution model with 20 components. X is a 10000-by-30 matrix of data generated from Mdl.
Specify the options for parallel computing.
stream = RandStream('mlfg6331_64'); % Random number stream options = statset('UseParallel',1,'UseSubstreams',1,... 'Streams',stream);
The input argument 'mlfg6331_64' of RandStream specifies to use the multiplicative lagged Fibonacci generator algorithm. options is a structure array with fields that specify options for controlling estimation.
Cluster the data using k-means clustering. Specify that there are k = 20 clusters in the data and increase the number of iterations. Typically, the objective function contains local minima. Specify 10 replicates to help find a lower, local minimum.
tic; % Start stopwatch timer [idx,C,sumd,D] = kmeans(X,20,'Options',options,'MaxIter',10000,... 'Display','final','Replicates',10);
Starting parallel pool (parpool) using the 'Processes' profile ... 08-Nov-2024 15:52:23: Job Queued. Waiting for parallel pool job with ID 2 to start ... Connected to parallel pool with 4 workers. Replicate 2, 56 iterations, total sum of distances = 7.62036e+06. Replicate 4, 79 iterations, total sum of distances = 7.62412e+06. Replicate 3, 76 iterations, total sum of distances = 7.62583e+06. Replicate 1, 94 iterations, total sum of distances = 7.60746e+06. Replicate 5, 103 iterations, total sum of distances = 7.61753e+06. Replicate 7, 77 iterations, total sum of distances = 7.61939e+06. Replicate 6, 96 iterations, total sum of distances = 7.6258e+06. Replicate 8, 113 iterations, total sum of distances = 7.60741e+06. Replicate 10, 66 iterations, total sum of distances = 7.62582e+06. Replicate 9, 80 iterations, total sum of distances = 7.60592e+06. Best total sum of distances = 7.60592e+06
toc % Terminate stopwatch timerElapsed time is 86.846475 seconds.
The Command Window indicates that six workers are available. The number of workers might vary on your system. The Command Window displays the number of iterations and the terminal objective function value for each replicate. The output arguments contain the results of replicate 9 because it has the lowest total sum of distances.
kmeans performs k-means clustering to partition data into k clusters. When you have a new data set to cluster, you can create new clusters that include the existing data and the new data by using kmeans. The kmeans function supports C/C++ code generation, so you can generate code that accepts training data and returns clustering results, and then deploy the code to a device. In this workflow, you must pass training data, which can be of considerable size. To save memory on the device, you can separate training and prediction by using kmeans and pdist2, respectively.
Use kmeans to create clusters in MATLAB® and use pdist2 in the generated code to assign new data to existing clusters. For code generation, define an entry-point function that accepts the cluster centroid positions and the new data set, and returns the index of the nearest cluster. Then, generate code for the entry-point function.
Generating C/C++ code requires MATLAB® Coder™.
Perform k-Means Clustering
Generate a training data set using three distributions.
rng('default') % For reproducibility X = [randn(100,2)*0.75+ones(100,2); randn(100,2)*0.5-ones(100,2); randn(100,2)*0.75];
Partition the training data into three clusters by using kmeans.
[idx,C] = kmeans(X,3);
Plot the clusters and the cluster centroids.
figure gscatter(X(:,1),X(:,2),idx,'bgm') hold on plot(C(:,1),C(:,2),'kx') legend('Cluster 1','Cluster 2','Cluster 3','Cluster Centroid')

Assign New Data to Existing Clusters
Generate a test data set.
Xtest = [randn(10,2)*0.75+ones(10,2);
randn(10,2)*0.5-ones(10,2);
randn(10,2)*0.75];Classify the test data set using the existing clusters. Find the nearest centroid from each test data point by using pdist2.
[~,idx_test] = pdist2(C,Xtest,'euclidean','Smallest',1);
Plot the test data and label the test data using idx_test by using gscatter.
gscatter(Xtest(:,1),Xtest(:,2),idx_test,'bgm','ooo') legend('Cluster 1','Cluster 2','Cluster 3','Cluster Centroid', ... 'Data classified to Cluster 1','Data classified to Cluster 2', ... 'Data classified to Cluster 3')

Generate Code
Generate C code that assigns new data to the existing clusters. Note that generating C/C++ code requires MATLAB® Coder™.
Define an entry-point function named findNearestCentroid that accepts centroid positions and new data, and then find the nearest cluster by using pdist2.
Add the %#codegen compiler directive (or pragma) to the entry-point function after the function signature to indicate that you intend to generate code for the MATLAB algorithm. Adding this directive instructs the MATLAB Code Analyzer to help you diagnose and fix violations that would cause errors during code generation.
type findNearestCentroid % Display contents of findNearestCentroid.m
function idx = findNearestCentroid(C,X) %#codegen [~,idx] = pdist2(C,X,'euclidean','Smallest',1); % Find the nearest centroid
Note: If you click the button located in the upper-right section of this page and open this example in MATLAB®, then MATLAB® opens the example folder. This folder includes the entry-point function file.
Generate code by using codegen (MATLAB Coder). Because C and C++ are statically typed languages, you must determine the properties of all variables in the entry-point function at compile time. To specify the data type and array size of the inputs of findNearestCentroid, pass a MATLAB expression that represents the set of values with a certain data type and array size by using the -args option. For details, see Specify Variable-Size Arguments for Code Generation.
codegen findNearestCentroid -args {C,Xtest}
Code generation successful.
codegen generates the MEX function findNearestCentroid_mex with a platform-dependent extension.
Verify the generated code.
myIndx = findNearestCentroid(C,Xtest); myIndex_mex = findNearestCentroid_mex(C,Xtest); verifyMEX = isequal(idx_test,myIndx,myIndex_mex)
verifyMEX = logical
1
isequal returns logical 1 (true), which means all the inputs are equal. The comparison confirms that the pdist2 function, the findNearestCentroid function, and the MEX function return the same index.
You can also generate optimized CUDA® code using GPU Coder™.
cfg = coder.gpuConfig('mex'); codegen -config cfg findNearestCentroid -args {C,Xtest}
For more information on code generation, see General Code Generation Workflow. For more information on GPU coder, see Get Started with GPU Coder (GPU Coder) and Supported Functions (GPU Coder).
The kmeans function ignores table rows that contain a missing value. To use all rows in the input data for k-means clustering, you can impute the missing values using a regression model.
Load the carbig data set and create a table that contains the Weight, Displacement, and Horsepower predictors.
load carbig
X = table(Weight,Displacement,Horsepower);Display the number of missing values in each column of X.
MissingValues = sum(ismissing(X))
MissingValues = 1×3
0 0 6
Column 3 (Horsepower) has six missing values. The other columns do not contain any missing values.
Train a multiple regression model using rows that do not contain missing values. Specify Horsepower as the response variable.
HPmodel = fitlm(rmmissing(X),"Horsepower");Display a plot of the regression model.
plot(HPmodel)

Impute the missing Horsepower values in X using the linear regression model.
imputedHP = predict(HPmodel,X(any(ismissing(X),2),1:2))
imputedHP = 6×1
70.6749
105.0360
65.2328
90.0460
73.9490
94.1612
Replace the missing Horsepower values with the imputed values.
X(any(ismissing(X),2),3) = table(imputedHP);
Cluster the data using k-means clustering. Specify that the data has three clusters.
[idx,C] = kmeans(table2array(X),3);
Plot the data and cluster assignments.
scatter3(X.Weight,X.Displacement,X.Horsepower,15,idx,"filled")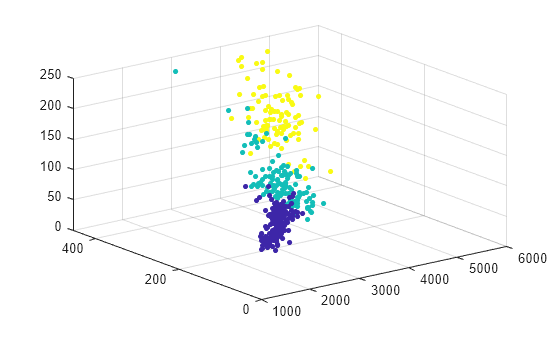
Input Arguments
Data, specified as a numeric matrix. The rows of X correspond
to observations, and the columns correspond to variables.
If X is a numeric vector, then kmeans treats
it as an n-by-1 data matrix, regardless of its
orientation.
The software treats NaNs in X as
missing data and removes any row of X that contains at
least one NaN. Removing rows of X
reduces the sample size. The kmeans function
returns NaN for the corresponding value in the output
argument idx.
Data Types: single | double
Number of clusters in the data, specified as a positive integer.
Data Types: single | double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: 'Distance','cosine','Replicates',10,'Options',statset('UseParallel',1) specifies
the cosine distance, 10 replicate clusters at different
starting values, and to use parallel computing.
Level of output to display in the Command Window, specified
as the comma-separated pair consisting of 'Display' and
one of the following options:
'final'— Displays results of the final iteration'iter'— Displays results of each iteration'off'— Displays nothing
When you specify 'iter', the software displays the
following information after each iteration:
Iteration number
Phase, where
1corresponds to the batch update phase, and2corresponds to the online update phase (see Algorithms)Number of points reassigned to a different cluster during the iteration
Sum of the point-to-cluster-centroid distances
Example: 'Display','final'
Distance metric, in p-dimensional space, used for
minimization, specified as the comma-separated pair consisting of
'Distance' and 'sqeuclidean',
'cityblock', 'cosine',
'correlation', or
'hamming'.
kmeans computes centroid clusters differently for
the supported distance metrics. This table summarizes the available
distance metrics. In each formula, x is an
observation (that is, a row of X) and
c is a centroid (a row vector).
| Distance Metric | Description | Formula |
|---|---|---|
'sqeuclidean' | Squared Euclidean distance (default). Each centroid is the mean of the points in the cluster. |
|
'cityblock' | Sum of absolute differences, that is, the L1 distance. Each centroid is the component-wise median of the points in a cluster. |
|
'cosine' | One minus the cosine of the included angle between points (treated as vectors). Each centroid is the mean of the points in the cluster, after the points are normalized to unit Euclidean length. |
|
'correlation' | One minus the sample correlation between points (treated as sequences of values). Each centroid is the component-wise mean of the points in the cluster, after the points are centered and normalized to zero mean and unit standard deviation. |
where
|
'hamming' | This metric is only suitable for binary data. It is the proportion of bits that differ. Each centroid is the component-wise median of points in that cluster. |
where I is the indicator function. |
Example: 'Distance','cityblock'
Action to take if a cluster loses all its member observations,
specified as the comma-separated pair consisting of 'EmptyAction' and
one of the following options.
| Value | Description |
|---|---|
'error' | Treat an empty cluster as an error. |
'drop' | Remove any clusters that become empty. |
'singleton' | Create a new cluster consisting of the one point furthest from its centroid (default). |
Example: 'EmptyAction','error'
Maximum number of iterations, specified as the comma-separated
pair consisting of 'MaxIter' and a positive integer.
Example: 'MaxIter',1000
Data Types: double | single
Online update flag, specified as the comma-separated pair consisting
of 'OnlinePhase' and 'off' or 'on'.
If OnlinePhase is on,
then kmeans performs an online update phase in
addition to a batch update phase. The online phase can be time consuming
for large data sets, but guarantees a solution that is a local minimum
of the distance criterion. In other words, the software finds a partition
of the data in which moving any single point to a different cluster
increases the total sum of distances.
Example: 'OnlinePhase','on'
Options for controlling the iterative algorithm for minimizing the fitting criteria, specified
as the comma-separated pair consisting of 'Options'
and a structure array returned by statset. Supported fields
of the structure array specify options for controlling the iterative
algorithm.
This table summarizes the supported fields. Note that the supported fields require Parallel Computing Toolbox™.
| Field | Description |
|---|---|
'Streams' | A
In this case, use a
cell array the same size as the parallel pool. If
a parallel pool is not open, then
|
'UseParallel' |
|
'UseSubstreams' | Set to true to compute in a
reproducible fashion. The default is
false. To compute reproducibly,
set Streams to a type allowing
substreams: 'mlfg6331_64' or
'mrg32k3a'. |
To ensure more predictable results, use parpool (Parallel Computing Toolbox) and explicitly
create a parallel pool before invoking kmeans and
setting 'Options',statset('UseParallel',1).
Example: 'Options',statset('UseParallel',1)
Data Types: struct
Number of times to repeat clustering using new initial cluster
centroid positions, specified as the comma-separated pair consisting
of 'Replicates' and an integer. kmeans returns
the solution with the lowest sumd.
You can set 'Replicates' implicitly by supplying
a 3-D array as the value for the 'Start' name-value
pair argument.
Example: 'Replicates',5
Data Types: double | single
Method for choosing initial cluster centroid positions (or seeds),
specified as the comma-separated pair consisting of
'Start' and 'cluster',
'plus', 'sample',
'uniform', a numeric matrix, or a numeric array.
This table summarizes the available options for choosing
seeds.
| Value | Description |
|---|---|
'cluster' | Perform a preliminary clustering phase on a
random 10% subsample of If the
number of observations in the random 10% subsample
is less than |
'plus' (default) | Select k seeds by implementing
the k-means++ algorithm
for cluster center initialization. |
'sample' | Select k observations from
X at random. |
'uniform' | Select k points uniformly at
random from the range of X. Not
valid with the Hamming distance. |
| numeric matrix | k-by-p
matrix of centroid starting locations. The rows of
Start correspond to seeds. The
software infers k from the first
dimension of Start, so you can
pass in [] for
k. |
| numeric array | k-by-p-by-r
array of centroid starting locations. The rows of
each page correspond to seeds. The third dimension
invokes replication of the clustering routine. Page
j contains the set of seeds for
replicate j. The software infers
the number of replicates (specified by the
'Replicates' name-value pair
argument) from the size of the third
dimension. |
Example: 'Start','sample'
Data Types: char | string | double | single
Output Arguments
Cluster indices, returned as a numeric column vector. idx has
as many rows as X, and each row indicates the cluster
assignment of the corresponding observation.
Within-cluster sums of point-to-centroid distances, returned as a numeric column vector.
sumd is a k-by-1 vector, where
element j is the sum of point-to-centroid distances
within cluster j. By default, kmeans
uses the squared Euclidean distance (see 'Distance'
metrics).
Distances from each point to every centroid, returned as a numeric matrix.
D is an
n-by-k matrix, where element
(j,m) is the distance from
observation j to centroid m. By
default, kmeans uses the squared Euclidean distance
(see 'Distance'
metrics).
More About
k-means clustering, or Lloyd’s algorithm [2], is an iterative, data-partitioning algorithm that assigns n observations to exactly one of k clusters defined by centroids, where k is chosen before the algorithm starts.
The algorithm proceeds as follows:
Choose k initial cluster centers (centroid). For example, choose k observations at random (by using
'Start','sample') or use the k-means ++ algorithm for cluster center initialization (the default).Compute point-to-cluster-centroid distances of all observations to each centroid.
There are two ways to proceed (specified by
OnlinePhase):Batch update — Assign each observation to the cluster with the closest centroid.
Online update — Individually assign observations to a different centroid if the reassignment decreases the sum of the within-cluster, sum-of-squares point-to-cluster-centroid distances.
For more details, see Algorithms.
Compute the average of the observations in each cluster to obtain k new centroid locations.
Repeat steps 2 through 4 until cluster assignments do not change, or the maximum number of iterations is reached.
The k-means++ algorithm uses an heuristic to find centroid seeds for k-means clustering. According to Arthur and Vassilvitskii [1], k-means++ improves the running time of Lloyd’s algorithm, and the quality of the final solution.
The k-means++ algorithm chooses seeds as follows, assuming the number of clusters is k.
Select an observation uniformly at random from the data set, X. The chosen observation is the first centroid, and is denoted c1.
Compute distances from each observation to c1. Denote the distance between cj and the observation m as .
Select the next centroid, c2 at random from X with probability
To choose center j:
Compute the distances from each observation to each centroid, and assign each observation to its closest centroid.
For m = 1,...,n and p = 1,...,j – 1, select centroid j at random from X with probability
where Cp is the set of all observations closest to centroid cp and xm belongs to Cp.
That is, select each subsequent center with a probability proportional to the distance from itself to the closest center that you already chose.
Repeat step 4 until k centroids are chosen.
Arthur and Vassilvitskii [1] demonstrate, using a simulation study for several cluster orientations, that k-means++ achieves faster convergence to a lower sum of within-cluster, sum-of-squares point-to-cluster-centroid distances than Lloyd’s algorithm.
Algorithms
kmeansuses a two-phase iterative algorithm to minimize the sum of point-to-centroid distances, summed over allkclusters.This first phase uses batch updates, where each iteration consists of reassigning points to their nearest cluster centroid, all at once, followed by recalculation of cluster centroids. This phase occasionally does not converge to solution that is a local minimum. That is, a partition of the data where moving any single point to a different cluster increases the total sum of distances. This is more likely for small data sets. The batch phase is fast, but potentially only approximates a solution as a starting point for the second phase.
This second phase uses online updates, where points are individually reassigned if doing so reduces the sum of distances, and cluster centroids are recomputed after each reassignment. Each iteration during this phase consists of one pass though all the points. This phase converges to a local minimum, although there might be other local minima with lower total sum of distances. In general, finding the global minimum is solved by an exhaustive choice of starting points, but using several replicates with random starting points typically results in a solution that is a global minimum.
If
Replicates= r > 1 andStartisplus(the default), then the software selects r possibly different sets of seeds according to the k-means++ algorithm.If you enable the
UseParalleloption inOptionsandReplicates> 1, then each worker selects seeds and clusters in parallel.
References
[1] Arthur, David, and Sergi Vassilvitskii. K-means++: The Advantages of Careful Seeding. In SODA ‘07: Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms, 1027–1035. Society for Industrial and Applied Mathematics, 2007.
[2] Lloyd, S. Least Squares Quantization in PCM. IEEE Transactions on Information Theory 28, no. 2 (March 1982): 129–37.
[3] Seber, G. A. F. Multivariate Observations. Hoboken, NJ: John Wiley & Sons, Inc., 1984.
[4] Spath, H. Cluster Dissection and Analysis: Theory, FORTRAN Programs, Examples. Translated by J. Goldschmidt. New York: Halsted Press, 1985.
Extended Capabilities
Usage notes and limitations:
Supported syntaxes are:
idx = kmeans(X,k)[idx,C] = kmeans(X,k)[idx,C,sumd] = kmeans(X,k)[___] = kmeans(___,Name,Value)
Supported name-value pair arguments, and any differences, are:
'Display'— Default value is'iter'.'MaxIter''Options'— Supports only the'TolFun'field of the structure array created bystatset. The default value of'TolFun'is1e-4. Thekmeansfunction uses the value of'TolFun'as the termination tolerance for the within-cluster sums of point-to-centroid distances. For example, you can specify'Options',statset('TolFun',1e-8).'Replicates''Start'— Supports only'plus','sample', and a numeric array.
For more information, see Tall Arrays for Out-of-Memory Data.
Usage notes and limitations:
If the
Startmethod uses random selections, the initial centroid cluster positions might not match MATLAB®.If the number of rows in
Xis fixed, code generation does not remove rows ofXthat contain aNaN.The cluster centroid locations in
Ccan have a different order than in MATLAB. In this case, the cluster indices inidxhave corresponding differences.If you provide
Display, its value must be'off'.If you provide
Streams, it must be empty andUseSubstreamsmust befalse.When you set the
UseParalleloption totrue:Some computations can execute in parallel even when
Replicatesis1. For large data sets, whenReplicatesis1, consider setting theUseParalleloption totrue.kmeansusesparfor(MATLAB Coder) to create loops that run in parallel on supported shared-memory multicore platforms. Loops that run in parallel can be faster than loops that run on a single thread. If your compiler does not support the Open Multiprocessing (OpenMP) application interface or you disable OpenMP library, MATLAB Coder™ treats theparfor-loops asfor-loops. To find supported compilers, see Supported Compilers.
To save memory on the device to which you deploy generated code, you can separate training and prediction by using
kmeansandpdist2, respectively. Usekmeansto create clusters in MATLAB and usepdist2in the generated code to assign new data to existing clusters. For code generation, define an entry-point function that accepts the cluster centroid positions and the new data set, and returns the index of the nearest cluster. Then, generate code for the entry-point function. For an example, see Assign New Data to Existing Clusters and Generate C/C++ Code.kmeansreturns integer-type (int32) indices in generated standalone C/C++ code. Therefore, the function allows for stricter single-precision support when you use single-precision inputs. For MEX code generation, the function still returns double-precision indices to match the MATLAB behavior.
For more information on code generation, see Introduction to Code Generation and General Code Generation Workflow.
To run in parallel, specify the Options name-value argument in the call to
this function and set the UseParallel field of the
options structure to true using
statset:
Options=statset(UseParallel=true)
For more information about parallel computing, see Run MATLAB Functions with Automatic Parallel Support (Parallel Computing Toolbox).
This function fully supports GPU arrays. For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Version History
Introduced before R2006a
See Also
linkage | clusterdata | incrementalKMeans | silhouette | parpool (Parallel Computing Toolbox) | statset | gmdistribution | kmedoids
External Websites
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)