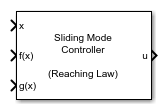
Sliding Mode Controller (Reaching Law)
Libraries:
Simulink Control Design /
Sliding Mode
Description
Sliding Mode Control (SMC) is a robust control strategy that brings the system state trajectory to a specified sliding surface and maintains it there. This approach is advantageous for systems requiring high levels of precision and robustness, especially in the presence of disturbances and uncertainties. Once the system reaches the sliding surface, SMC ensures that it stays on this path despite any external or internal changes to system dynamics.
The Sliding Mode Controller block enables you to implement SMC for nonlinear systems characterized by the equation . Using this block, you can create a compensator which uses a reaching law, a method that dynamically adjusts control actions to guide the system states toward the sliding surface efficiently. The block provides the following two modes of operation:
Regulation mode
Tracking mode
Here, C is the sliding coefficient matrix, s(x) is the switching function, and h(s(x)) is the reaching law.
Additionally, SMC minimizes chattering effects, a common challenge in control systems characterized by rapid oscillation or high-frequency switching of the control signal. The block allows you to customize the sliding surface and adjust the reaching law parameters. This enables you to tune the control strategy to your specific system dynamics and objectives, enhancing the system stability and response under varying conditions.
For more information about SMC, see Sliding Mode Control.
Examples
Ports
Input
Output
Parameters
Extended Capabilities
Version History
Introduced in R2024b