p681LMSChannel
Filter input signal through ITU-R P.681 LMS frequency-flat fading channel
Since R2022a
Description
The p681LMSChannel
System object™ filters a real or complex input signal through a frequency-flat fading land
mobile-satellite (LMS) communication channel, as defined in these recommendations.
For details, refer to More About.
To filter an input signal through a P.681-11 LMS time-varying channel:
Create the
p681LMSChannelobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Creation
Description
chan = p681LMSChannel
The default System object has the environment set to an urban scenario, with carrier frequency of 2.2 GHz and an elevation angle of 45 degrees. This object models a single geostationary satellite.
chan = p681LMSChannel(Name=Value)SampleRate=20e3 sets the input
signal sample rate to 20e3.
Properties
Unless otherwise indicated, properties are nontunable, which means you cannot change their
values after calling the object. Objects lock when you call them, and the
release function unlocks them.
If a property is tunable, you can change its value at any time.
For more information on changing property values, see System Design in MATLAB Using System Objects.
Since R2024b
Number of channel states, specified as one of these values.
2— Sets the channel as a two-state semi-Markov channel, as specified in the ITU-R P.681-11 specification.3— Sets the channel as a three-state semi-Markov channel, as specified in the ITU-R P.681-7 specification.
Data Types: double | int8
Input signal sample rate in hertz, specified as a positive scalar.
Data Types: double
Initial state of the channel, specified as one of these values.
"Good""Moderate"— Applicable only when NumStates is set to3."Bad"
When you set NumStates
property to 3, "Good" refers to State
A or Clear Line-of-sight (LOS) conditions, "Moderate"
refers to State B or slightly shadowed conditions, and
"Bad" refers to State C or fully blocked
conditions.
Data Types: char | string
Carrier frequency in hertz, specified as a nonnegative scalar.
Data Types: double
Path elevation angle to a geostationary satellite in degrees, specified as a scalar. The nominal value is in the range [0, 90].
Data Types: double
Speed of mobile terminal in m/s, specified as a nonnegative scalar. The default
value of 0.8333 m/s translates to 3 km/h.
This property affects the Doppler spread applied to the multipath component and also the Doppler shift applied to the direct path component.
Note
For a static channel, set MobileSpeed and SatelliteDopplerShift properties to 0. In this case,
the Doppler spread is not applicable for the multipath component and the Doppler shift
is also not applied in direct path component of the channel.
Also, to generate a new channel realization for a static channel, either reset the
object by calling the reset function or set
the SatelliteDopplerShift property to a nonzero value.
Data Types: double
Azimuth orientation in degrees, specified as a scalar. This value specifies the direction of movement of the ground or mobile terminal. The nominal value is in the range [0, 360].
When you set this property to odd multiples of 90, the Doppler shift caused by the mobile movement in the direct path component is nonexistent.
Data Types: double
Since R2024a
Doppler shift due to the satellite movement in hertz, specified as a scalar.
Satellite Doppler shift calculations account for the satellite altitude, satellite elevation angle, carrier frequency, and satellite velocity.
The default value of 0 Hz corresponds to the Doppler shift due to a satellite with an elevation angle of 90 degrees.
Note
For a static channel, set the MobileSpeed and SatelliteDopplerShift properties to
0. In static channels, the Doppler spread is not applicable for
the multipath component, and the Doppler shift does not apply to the direct path
component of the channel.
To generate a new channel realization for a static channel, either reset the
object by calling the reset function, or set
the SatelliteDopplerShift property to a nonzero value.
Tunable: Yes
Data Types: double
Type of propagation environment, specified as one of these values.
"Urban""Suburban""RuralWooded""Village""Residential""Highway"— Applicable only when you set the value of CarrierFrequency property in the range [10, 20] GHz"Rural"— Applicable only when you set the value of CarrierFrequency property in the range [10, 20] GHz"Train"— Applicable only when you set the value of CarrierFrequency property in the range [10, 20] GHz"Custom"
When you set this property to "Custom" and NumStates
property to 2, configure the propagation environment using these properties.
Dependencies
To enable this property, set the NumStates
property to 2.
Data Types: char | string
Parameters of the state duration distribution in dB, specified as one of these values.
2-by-2 matrix — Applicable when you set the NumStates property to
2and Environment property to"Custom".For example, if you specify the input as [muG, muB; sigmaG, sigmaB], then:
muG and sigmaG represent the mean and standard deviation of good state duration, respectively.
muB and sigmaB represent the mean and standard deviation of bad state duration, respectively.
2-by-3 matrix— Applicable when you set the NumStates property to
3.For example, if you specify the input as [beta,muM,muB; gamma,sigmaM,sigmaB], then:
beta and gamma define the parameters for the good state distribution. This channel uses the linear value of beta or gamma, which is,
exp(beta) orexp(gamma), respectively.muM and sigmaM represent the mean and standard deviation of moderate state duration, respectively.
muB and sigmaB represent the mean and standard deviation of bad state duration, respectively.
Dependencies
To enable this property, set either of these conditions.
Set the NumStates property to
3.Set the NumStates property to
2and Environment property to"Custom".
Data Types: double
Minimum duration of each state in meters, specified as a two-element row vector. The first element corresponds to good state and the second element corresponds to bad state.
Dependencies
To enable this property, set the NumStates
property to 2 and Environment property to "Custom".
Data Types: double
Parameters of direct path amplitude distribution in dB, specified as one of these values.
2-by-2 matrix — Applicable when you set the NumStates property to
2and Environment property to"Custom".For example, if you specify the input as [muMaG, muMaB; sigmaMaG, sigmaMaB], then:
muMaG and sigmaMaG represent the mean of the direct path amplitude (Ma) and the standard deviation of Ma in good state, respectively.
muMaB and sigmaMaB represent the mean and standard deviation of Ma in bad state, respectively.
2-by-1 vector — Applicable when you set the NumStates property to
3.For example, if you specify the input as [muMaM; sigmaMaM], then muMaM and sigmaMaM represent the mean and standard deviation of direct path amplitude in the moderate state, respectively.
Dependencies
To enable this property, set either of these conditions.
Set the NumStates property to
3.Set the NumStates property to
2and Environment property to"Custom".
Data Types: double
Mean multipath power of each state in dB, specified as a 1-by-3 vector.
For example, if you specify the input as [Mg, Mm, Mb], then Mg represents the mean multipath power in the good state, Mm represents the mean multipath power in the moderate state, and Mb represents the mean multipath power in the bad state.
Dependencies
To enable this property, set the NumStates
property to 3.
Data Types: double
Coefficients to compute the multipath power, specified as a 2-by-2 matrix. For example, if you specify the input as [h1G, h1B; h2G, h2B], then:
h1G and h2G represent the coefficients in good state.
h1B and h2B represent the coefficients in bad state.
Dependencies
To enable this property, set the NumStates
property to 2 and Environment property to "Custom".
Data Types: double
Coefficients to compute standard deviation of direct path amplitude in all states, specified as a 2-by-2 matrix. For example, if you specify the input as [g1G, g1B; g2G, g2B], then:
g1G and g2G represent the coefficients in good state.
g1B and g2B represent the coefficients in bad state.
Dependencies
To enable this property, set the NumStates
property to 2 and Environment property to "Custom".
Data Types: double
Direct path amplitude correlation distance (Lcorr) in meters, specified as one of these values.
Two-element row vector — Applicable when you set the NumStates property to
2and Environment property to"Custom". The first element corresponds to good state and the second element corresponds to bad state.Scalar — Applicable when you set the NumStates property to
3. The value represents Lcorr of moderate state.
Dependencies
To enable this property, set either of these conditions.
Set the NumStates property to
3.Set the NumStates property to
2and Environment property to"Custom".
Data Types: double
Coefficients to compute the transition length (f1;f2), specified as a two-element column vector.
Dependencies
To enable this property, set the NumStates
property to 2 and Environment property to "Custom".
Data Types: double
Minimum and maximum probability of each state, specified as a 2-by-2 matrix. For example, if you specify the input as [pminG, pminB; pmaxG, pmaxB], then:
pminG and pmaxG represent the minimum and maximum values of state probability in good state.
pminB and pmaxB represent the minimum and maximum values of state probability in bad state.
The minimum probability must be less than the maximum probability in a state. The value of each element must be in range [0, 1].
Dependencies
To enable this property, set the NumStates
property to 2 and Environment property to "Custom".
Data Types: double
State transition probability matrix, specified as a 3-by-3 matrix.
For example, if you specify the matrix as [Pgg Pgm Pgb; Pmg Pmm Pmb; Pbg Pbm Pbb], then Pxy represents the probability of the next state as y when the current state is x. In the matrix, g represents good state, m represents moderate state, and b represents bad state.
Elements in the matrix must be in the range [0, 1]. The sum of the elements in each row of the matrix must be equal to 1.
Dependencies
To enable this property, set the NumStates
property to 3.
Data Types: double
Channel filtering, specified as one of these logical values.
1(true) — The object accepts an input signal and produces a filtered output signal, in addition to the channel path gains, sample times, and state series.0(false) — The object does not accept an input signal, produces no filtered output signal, and outputs only channel path gains, sample times, and state series. You must specify the duration of the fading process by using the NumSamples property, and the sampling rate by using the SampleRate property.
Data Types: logical
Number of time samples used to set the duration of the fading process realization, specified as a nonnegative integer.
Tunable: Yes
Dependencies
To enable this property, set ChannelFiltering property to false.
Data Types: double
Data type of outputs, specified as one of these values.
"double""single"
Dependencies
To enable this property, set ChannelFiltering property to false.
Data Types: char | string
Channel model fading technique, specified as "Filtered Gaussian noise" or "Sum of sinusoids".
Data Types: char | string
Number of sinusoids used to generate the Doppler fading samples, specified as a positive integer.
Dependencies
To enable this property, set the FadingTechnique property to "Sum of
sinusoids".
Data Types: double | uint16
Source of the random number stream, specified as "Global stream"
or "mt19937ar with seed".
When you specify
"Global stream", the object uses the current global random number stream for uniformly and normally distributed random number generation. In this case, theresetobject function resets only the filters.When you specify
"mt19937ar with seed", the object uses the mt19937ar algorithm for uniformly and normally distributed random number generation. In this case, theresetobject function resets the filters and reinitializes the random number stream to the value of the Seed property.
Data Types: char | string
Initial seed of the mt19937ar random number stream generator algorithm, specified as
a nonnegative integer. When you call the reset object function, it reinitializes the mt19937ar random number stream
to the Seed value.
Dependencies
To enable this property, set the RandomStream property to "mt19937ar with
seed".
Data Types: double | uint32
Channel visualization, specified as one of these options.
"Off""Impulse response""Frequency response""Impulse and frequency responses""Doppler spectrum"
When you set this property to enable the visualization, selected channel characteristics are animated in separate figures, with each System object call.
For more information, see Channel Visualization.
Data Types: char | string
Usage
Description
[
produces path gains, pathgains,sampletimes,stateseries] = chan()pathgains, sample times,
sampletimes, and state series, stateseries for
an ITU-R P.681 LMS flat fading channel.
In this case, the System object acts as a source of path gains, sample times, and state series.
Specify the duration of the fading process by using the NumSamples property. Specify the datatype of outputs using the OutputDataType property.
Note
This syntax is applicable when you set the ChannelFiltering property to false.
[
filters the input signal, y,pathgains,sampletimes,stateseries] = chan(x)x, through an ITU-R P.681 LMS flat fading
channel, and returns the output channel-impaired signal in y, in
addition to the outputs in the previous syntax.
Note
This syntax is applicable when you set the ChannelFiltering property to true.
Input Arguments
Input signal, specified as an NS-by-1 vector, where NS is the number of input samples.
Data Types: single | double
Complex Number Support: Yes
Output Arguments
Output signal, returned as an NS-by-1
vector of complex values with the same data precision and length as the input signal
x.
NS is the number of input
samples.
Data Types: single | double
Complex Number Support: Yes
Channel path gains of fading process, returned as an NS-by-1 vector of complex values.
When you set the ChannelFiltering property to
true,pathgainsis of the same data precision as the input signalx, and NS is the number of input samples.When you set the ChannelFiltering property to
false,pathgainsis of the same data precision as the OutputDataType property and NS is equal to the NumSamples property.
Data Types: single | double
Complex Number Support: Yes
Sample times of channel snapshots, returned as an NS-by-1 vector.
When you set the ChannelFiltering property to
true,sampletimesis of the same data precision as the input signalx, and NS is the number of input samples.When you set the ChannelFiltering property to
false,sampletimesis of the same data precision as the OutputDataType property and NS is equal to the NumSamples property.
Data Types: single | double
State series of the channel, returned as an NS-by-1 vector.
When you set the ChannelFiltering property to
true,stateseriesis of the same data precision as the input signalx, and NS is the number of input samples.When you set the ChannelFiltering property to
false,stateseriesis of the same data precision as the OutputDataType property and NS is equal to the NumSamples property.
Each value of this vector describes the state in which channel is present for that channel snapshot.
When you set the NumStates property to
2— A value of0represents bad state. A value of1represents good state. A value between 0 and 1 represents a state transition.When you set the NumStates property to
3— A value of0refers to bad state, value of0.5refers to moderate state, and value of1refers to good state. In a three-state channel, the transitions from one state to another state are abrupt, therefore, at any point of time the value of the state series can be0,0.5, or1.
Data Types: single | double
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
Examples
Create and Configure the Channel
Create an ITU-R P.681-11 LMS channel and configure it for a suburban scenario with a carrier frequency of 20 GHz and an elevation angle of 50 degrees. Set the sample rate to 6000 kHz.
Specify the mobile terminal speed to 50 m/s, with an azimuth orientation of 20 degrees.
chan = p681LMSChannel; chan.SampleRate = 6e6; % Hz chan.CarrierFrequency = 20e9; % Hz chan.ElevationAngle = 50; % degrees chan.Environment = "Suburban"; chan.MobileSpeed = 50; % m/s chan.AzimuthOrientation = 20; % degrees
Display the channel characteristics.
disp(chan)
p681LMSChannel with properties:
NumStates: 2
SampleRate: 6000000
InitialState: "Good"
CarrierFrequency: 2.0000e+10
ElevationAngle: 50
MobileSpeed: 50
AzimuthOrientation: 20
SatelliteDopplerShift: 0
Environment: "Suburban"
ChannelFiltering: true
Show all properties
Transmit Input Signal Through Channel
Set the random number generation seed as default.
rng("default")Generate a random QPSK-modulated input signal.
numSamples = 6e6;
txWaveform = pskmod(randi([0 3],numSamples,1),4); % Modulation order = 4Filter the signal through the channel.
[rxWaveform,pathGains,sampleTimes,stateSeries] = chan(txWaveform);
Visualize Space Series and State Series
Plot the space series as a function of time.
figure % Create figure window subplot(2,1,1) plot(sampleTimes,20*log10(abs(pathGains))) title("Space Series") xlabel("Time (in s)") ylabel("Path Gain (in dB)") grid on
Plot the state series as a function of time.
subplot(2,1,2) plot(sampleTimes,stateSeries) title("State Series") xlabel("Time (in s)") ylabel("State") grid on

Define the channel configuration using a p681LMSChannel System object and specify its properties.
Set the number of channel states to 3, visualization as Doppler spectrum, and disable the channel filtering.
chan = p681LMSChannel; chan.NumStates = 3; chan.SampleRate = 450000; % Hz chan.InitialState = "Moderate"; chan.CarrierFrequency = 11e9; % Hz chan.ElevationAngle = 50; % degrees chan.MobileSpeed = 20; % m/s chan.SatelliteDopplerShift = 25e2; % Hz chan.Visualization = "Doppler spectrum"; chan.ChannelFiltering = false; chan.NumSamples = 4e7;
Display the channel characteristics.
disp(chan)
p681LMSChannel with properties:
NumStates: 3
SampleRate: 450000
InitialState: "Moderate"
CarrierFrequency: 1.1000e+10
ElevationAngle: 50
MobileSpeed: 20
AzimuthOrientation: 0
SatelliteDopplerShift: 2500
StateDistribution: [2×3 double]
DirectPathDistribution: [2×1 double]
MultipathPower: [-14 -15 -20]
DirectPathCorrelationDistance: 3.2293
StateTransitionMatrix: [3×3 double]
ChannelFiltering: false
NumSamples: 40000000
OutputDataType: "double"
Show all properties
Get the path gains, sample times, and state series of the channel. Also, observe the Doppler spectrum.
[pathGains,sampleTimes,stateSeries] = chan();

Get channel information from a p681LMSChannel System object by using the info object function.
Create an ITU-R P.681-11 LMS channel System object and specify its properties.
chan = p681LMSChannel; chan.SampleRate = 10e3; % Hz chan.MobileSpeed = 2; % m/s chan.Environment = "RuralWooded"; disp(chan)
p681LMSChannel with properties:
NumStates: 2
SampleRate: 10000
InitialState: "Good"
CarrierFrequency: 2.2000e+09
ElevationAngle: 45
MobileSpeed: 2
AzimuthOrientation: 0
SatelliteDopplerShift: 0
Environment: "RuralWooded"
ChannelFiltering: true
Show all properties
QPSK-modulate a random input signal, and then pass it through the channel.
numSamples = 2e4; txWaveform = pskmod(randi([0 3],numSamples,1),4); [rxWaveform,pathGains,sampleTimes,stateSeries] = chan(txWaveform);
Get the characteristic information about the P.681-11 LMS channel.
info(chan)
ans = struct with fields:
PathDelays: 0
ChannelFilterDelay: 0
ChannelFilterCoefficients: 1
NumSamplesProcessed: 20000
Transmit another QPSK-modulated random input signal through the channel
numSamples2 = 3e4; txWaveform2 = pskmod(randi([0 3],numSamples2,1),4); [rxWaveform2,pathGains2,sampleTimes2,stateSeries2] = chan(txWaveform2);
Observe the change in number of samples processed.
info(chan)
ans = struct with fields:
PathDelays: 0
ChannelFilterDelay: 0
ChannelFilterCoefficients: 1
NumSamplesProcessed: 50000
More About
To calculate the Doppler spread and Doppler shift due to the movement of the mobile on Earth, refer to these formulas.
The maximum Doppler spread due to mobile movement is given by the following formula:
Fmob_max_spread = (vmob*fc) / c
where:
vmob is the speed of the mobile terminal on Earth in m/s, specified as the MobileSpeed property.
fc is the carrier frequency in Hz, specified by the CarrierFrequency property.
c is the speed of light in free space in m/s, specified as
physconst('lightspeed').
The Doppler shift due to mobile movement is given by the following formula:
fdmob = Fmob_max_spread *
cosd(θ) *cosd(φ)where:
Fmob_max_spread is the maximum Doppler spread due to mobile movement.
θ is the path elevation angle to the satellite in degrees, specified by the ElevationAngle property.
φ is the azimuth orientation in degrees, specified by the AzimuthOrientation property.
The sum of absolute value of SatelliteDopplerShift property and maximum Doppler shift caused by the mobile movement must be less than one-tenth of SampleRate property.
To estimate the performance of a LMS receiver, you must perform stochastic synthesis of realistic time series of the channel complex envelope. Use the semi-Markov enhanced 2-state model to simulate the LMS time-variations of the channel for a single geosynchronous satellite.
The figure shows a Loo time series generator which you can use to produce complex signal
variations. The parameters of the circuit update for the generations of time series in each
state. Inside a transition, the Loo parameters drawn for the Good and
Bad states around the transition are interpolated linearly in
dB.
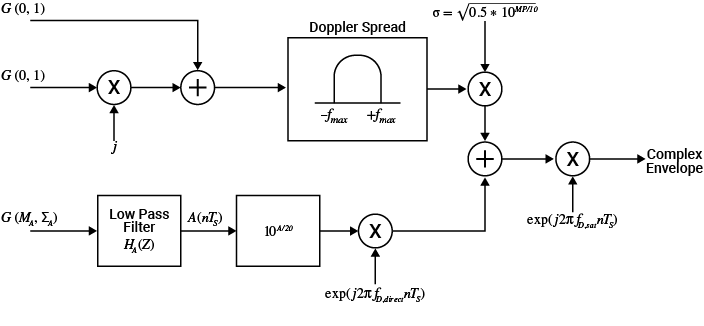
The upper half of the block diagram generates the multipath fast variations. The lower half shows the direct signal slow variations.
Generate multipath fast variations — In the upper half of the block diagram, the two zero-mean and unit-standard deviation Gaussian series in quadrature are passed through a unit-energy Doppler filter. Fast variations are ruled by the Doppler spread mainly due to the motion of the mobile terminal. You can use a Jakes model to generate the fast variations. This expression defines the Jakes filter:
for -fm < f < +fm
S(f) = 0 for -fm > f > +fm
After the Doppler spread, the resultant complex series is multiplied by σ, where 2σ2 is the mean square value of the multipath variations
Generate direct signal slow variations — The lower rail simulates the amplitude and phase variations of the direct signal. In the first step, generate a Gaussian distribution with mean MA (dB) and standard deviation ΣA (dB). In the second step, the series, in dB units, is converted to linear units. In the third step, introduce the phase variations in the direct signal. These are assumed to be linearly varying giving rise to a constant Doppler spectral line that depends on the relative mobile-satellite velocity and the angle of arrival, azimuth and elevation, with respect to the mobile trajectory.
The direct signal's amplitude is subjected to variations slower than those due to multipath caused by shadowing. In this implementation, the rate of change of the slow variations is characterized by the DirectPathCorrelationDistance property value, Lcorr. The sampling distance of the multipath being vmTs, generate the correlated shadowing time series by using this numerical low pass filter:
, where
vm is the speed of the mobile terminal, specified by the MobileSpeed property.
Ts is the sample time, given by 1/SampleRate property.
Generate Doppler variations due to satellite movement — Multipath fast variations and direct signal slow variations combine to form a complex envelope due to scattering environment and mobile movement. The complex envelope introduces variations in signal due to satellite movement, thereby forming the channel output.
The block diagram show these variables for Doppler variations:
fmax denotes the maximum Doppler spread due to mobile movement and is given by the following formula:
fmax = Fmob_max_spread = (vmob*fc) / c
where:
vmob is the speed of the mobile terminal on Earth in m/s, specified as the MobileSpeed property.
fc is the carrier frequency in Hz, specified by the CarrierFrequency property.
c is the speed of light in free space in m/s, specified as
physconst('lightspeed').
fD,direct is the Doppler shift due to mobile movement and is given by the following formula:
fD,direct = fdmob = Fmob_max_spread *
cosd(θ) *cosd(φ)where:
Fmob_max_spread is the maximum Doppler spread due to mobile movement.
θ is the path elevation angle to the satellite in degrees, specified by the ElevationAngle property.
φ is the azimuth orientation in degrees, specified by the AzimuthOrientation property.
fD,sat is the Doppler shift due to satellite movement, specified by the SatelliteDopplerShift property.
References
[1] ITU-R Recommendation P.681-11 (08/2019). “Propagation data required for the design systems in the land mobile-satellite service.” P Series; Radiowave propagation.
[2] ITU-R Recommendation P.681-7 (10/2009). “Propagation data required for the design of Earth-space land mobile telecommunication systems.” P Series; Radiowave propagation.
Extended Capabilities
Usage notes and limitations:
Code generation is available only when the
Visualizationproperty is"Off".See System Objects in MATLAB Code Generation (MATLAB Coder).
Version History
Introduced in R2022aThe p681LMSChannel
System object now supports the three-state LMS channel, as defined in the ITU-R
P.681-7.
Use the SatelliteDopplerShift property to specify the Doppler shift
due to the satellite movement in hertz.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)