range2height
Description
tgtht = range2height(r,anht,el)tgtht as a function of the propagated range
r, the sensor height anht, and the local
elevation angle el assuming a Curved Earth Model with a 4/3 effective Earth
radius.
tgtht = range2height(r,anht,el,Name=Value)
Examples
Determine the target height in meters given a range of 300 km, a sensor height of 10 meters, and an elevation angle of 0.5 degrees. Assume a curved Earth with an effective radius equal to 4/3 times the Earth's actual radius.
R = 300e3; anht = 10; el = 0.5; range2height(R,anht,el)
ans = 7.9325e+03
Compute target heights in meters using different Earth models and compare the values you obtain. Assume a range of 200 km and an antenna height of 100 meters. Use a range of elevation angles from 0 to 5 degrees.
R = 200e3; anht = 100; el = (0:0.1:5)';
Compute the target height for the given parameters assuming a flat Earth.
tgthtFlat = range2height(R,anht,el,Method="Flat");Compute the target height for the given parameters assuming free-space propagation with a curved Earth.
r0 = physconst("EarthRadius"); tgthtFS = range2height(R,anht,el,Method="Curved", ... EffectiveEarthRadius=r0);
Compute the target height for the given parameters assuming a 4/3 effective Earth radius.
tgthtEffRad = range2height(R,anht,el);
Compute the target height for the given parameters assuming the CRPL atmospheric model.
tgthtCRPL = range2height(R,anht,el,Method="CRPL");Plot the results.
plot(el,[tgthtFlat(:) tgthtFS(:) tgthtEffRad(:)], ... el,tgthtCRPL,'--',LineWidth=1.5) grid on xlabel("Elevation Angle (degrees)") ylabel("Target Height (m)") legend(["Flat" "Free Space" "4/3 Earth" "CRPL"],Location="best") title("Target Height Estimation")

Input Arguments
Propagated range between the target and the sensor in meters, specified as a
real-valued scalar or vector. If r is a vector, it must have the
same size as the other vector input arguments of
range2height.
Data Types: double
Sensor height in meters, specified as a nonnegative real-valued scalar or vector. If
anht is a vector, it must have the same size as the other
vector input arguments of range2height. Heights are referenced to
the ground.
Data Types: double
Local elevation angle in degrees, specified as a real-valued scalar or vector. The local elevation angle is the initial elevation angle of the ray leaving the sensor. If el is a vector, it must have the same size as the other vector input arguments of range2height.
Data Types: double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: Method="CRPL",SurfaceRefractivity=300,RefractionExponent=0.15,MaxNumIterations=8,Tolerance=1e-7
Earth model used for the computation, specified as "Curved",
"Flat", or "CPRL".
"Curved"— Assumes a Curved Earth Model with a 4/3 effective Earth radius, which is an approximation used for modeling refraction effects in the troposphere. To specify another value for the effective Earth radius, use theEffectiveEarthRadiusname-value argument."Flat"— Assumes a Flat Earth Model. In this case, the effective Earth radius is infinite."CRPL"— Assumes a curved Earth model with the atmosphere defined by the CRPL Exponential Reference Atmosphere Model with a refractivity of 313 N-units and a refraction exponent of 0.143859 km–1. To specify other values for the refractivity and the refraction exponent, use theSurfaceRefractivityandRefractionExponentname value arguments. This method requireselto be positive. For more information, see CRPL Model Geometry.
Data Types: char | string
Effective Earth radius in meters, specified as a positive scalar. If this argument is
not specified, range2height calculates the effective Earth radius
using a refractivity gradient of –39 × 10–9 N-units/meter,
which results in approximately 4/3 of the real Earth radius. This argument applies only
if Method is specified as "Curved".
Data Types: double
Surface refractivity in N-units, specified as a nonnegative real-valued scalar. The surface
refractivity is a parameter of the CRPL Exponential Reference Atmosphere Model used by
range2height. This argument applies only if
Method is specified as "CRPL".
Data Types: double
Refraction exponent, specified as a nonnegative real-valued scalar. The refraction exponent is
a parameter of the CRPL Exponential Reference Atmosphere Model used by
range2height. This argument applies only if
Method is specified as "CRPL".
Data Types: double
Maximum number of iterations for the CRPL method, specified as a nonnegative
scalar integer. This input acts as a safeguard to preempt long iterative calculations.
This argument applies only if Method is specified as
"CRPL".
If MaxNumIterations is set to 0,
range2height performs a faster but less accurate noniterative
CRPL calculation. The noniterative calculation has a maximum height error of 0.056388
m (0.185 ft) at a target height of 30,480 m (100,000 ft) and an elevation angle of 0.
The height error for the noniterative method decreases with decreasing target height
and increasing elevation angle.
Data Types: double
Numerical tolerance for the CRPL method, specified as a positive real scalar. The
iterative process terminates when the numerical tolerance is achieved. This argument
applies only if Method is specified as "CRPL"
and MaxNumIterations is greater than 0.
Data Types: double
Output Arguments
Target height in meters, returned as a nonnegative real-valued scalar or row vector.
If tgtht is a vector, it has the same size as the vector input
arguments of range2height. The height is referenced to the
ground.
More About
The flat Earth model assumes that the Earth has infinite radius and that the index of refraction of air is uniform throughout the atmosphere. The flat Earth model is applicable over short distances and is used in applications like communications, automotive radar, and synthetic aperture radar (SAR).
Given the antenna height ha and the initial elevation angle θ0, the model relates the target height hT and the slant range RT by
so knowing one of those magnitudes enables you to compute the other. The actual range R is equal to the slant range. The true elevation angle θT is equal to the initial elevation angle.
To compute the ground range G, use
The fact that the index of refraction of air depends on height can be treated approximately by using an effective Earth's radius larger than the actual value.
Given the effective Earth's radius R0, the antenna height ha, and the initial elevation angle θ0, the model relates the target height hT and the slant range RT by
so knowing one of those magnitudes enables you to compute the other. In particular,
The actual range R is equal to the slant range. The true elevation angle θT is equal to the initial elevation angle.
To compute the ground range G, use
A standard propagation model uses an effective Earth's radius that is 4/3 times the actual value. This model has two major limitations:
The model implies a value for the index of refraction near the Earth's surface that is valid only for certain areas and at certain times of the year. To mitigate this limitation, use an effective Earth's radius based on the near-surface refractivity value.
The model implies a value for the gradient of the index of refraction that is unrealistically low at heights of around 8 km. To partially mitigate this limitation, use an effective Earth's radius based on the platform altitudes.
For more information, see effearthradius.
Atmospheric refraction evidences itself as a deviation in an electromagnetic ray from a straight line due to variation in air density as a function of height. The Central Radio Propagation Laboratory (CRPL) exponential reference atmosphere model treats refraction effects by assuming that the index of refraction n(h) and the refractivity N decay exponentially with height. The model defines
where Ns is the atmospheric refractivity value (in units of 10–6) at the surface of the earth, Rexp is the decay constant, and h is the height above the surface in kilometers. Thus
The default value of Ns is 313
N-units and can be modified using the SurfaceRefractivity name-value
argument in functions that accept it. The default value of
Rexp is 0.143859 km–1 and can be modified using the RefractionExponent
name-value argument in functions that accept it.
When the refractivity of air is incorporated into the curved Earth model, the ray paths do not follow a straight line but curve downward. (This statement assumes standard atmospheric propagation and nonnegative elevation angles.) The true elevation angle 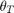 is different from the initial
is different from the initial  . The actual range
. The actual range 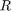 , which is the distance along the curved path
, which is the distance along the curved path  , is different from the slant range
, is different from the slant range 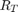 .
.
Given the Earth's radius  , the antenna height
, the antenna height 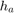 , the initial elevation angle
, the initial elevation angle  , and the height-dependent index of refraction
, and the height-dependent index of refraction 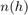 with value
with value  at
at 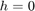 , the modified model relates the target height
, the modified model relates the target height 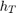 and the actual range
and the actual range 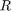 by
by

When Method is specified as "CRPL", the integral is solved using 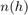 from CRPL Exponential Reference Atmosphere Model.
from CRPL Exponential Reference Atmosphere Model.
To compute the ground range 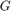 , use
, use


References
[1] Barton, David K. Radar Equations for Modern Radar. Norwood, MA: Artech House, 2013.
[2] Bean, B.R., and G.D. Thayer. "Central Radio Propagation Laboratory Exponential Reference Atmosphere." Journal of Research of the National Bureau of Standards, Section D: Radio Propagation 63D, no. 3 (November 1959): 315. https://doi.org/10.6028/jres.063D.031.
[3] Blake, Lamont V. "Ray Height Computation for a Continuous Nonlinear Atmospheric Refractive-Index Profile." Radio Science 3, no. 1 (January 1968): 85–92. https://doi.org/10.1002/rds19683185.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
Version History
Introduced in R2021b
See Also
Apps
Functions
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)