height2range

Convert target height to propagated range

Since R2021b

Syntax

r = height2range(tgtht,anht,el)

r = height2range(tgtht,anht,el,Name=Value)

[r,sr,t_el] = height2range(___,Method="CRPL")

Description

r = height2range(tgtht,anht,el) returns the propagated range to the target, r, as a function of the target height tgtht, the sensor height anht, and the elevation angle of the sensor el, assuming a Curved Earth Model with a 4/3 effective Earth radius factor. r is the distance along the slightly curved propagated path that results from atmospheric refraction and is longer than the straight-line geometric distance between the sensor and target.

r = height2range(tgtht,anht,el,Name=Value) specifies additional inputs using name-value arguments. For example, you can specify a flat Earth model, a curved Earth model with a given radius, or a CRPL Exponential Reference Atmosphere Model with custom values.

[r,sr,t_el] = height2range(___,Method="CRPL") also returns the straight-line slant range between the target and the sensor, sr, and the elevation angle between the target and the propagated path r, t_el. This syntax is valid when you specify the Earth model as "CRPL".

Examples

Range Along Propagated Path

Compute the range along the propagated path for a target height of 1 km, an antenna height of 10 meters, and an elevation angle of 2 degrees at the radar. Assume a curved Earth model with a 4/3 effective Earth radius.

r = height2range(1e3,10,2)

r = 
2.7125e+04

Propagated Range Using CRPL Atmosphere

Compute the range along the propagated path using the CRPL exponential reference atmosphere. Assume a target height of 1 km, an antenna height of 10 meters, and an elevation angle of 2 degrees at the radar. Additionally, compute the true slant range and the true elevation angle to the target.

[R,SRtrue,elTrue] = height2range(1e3,10,2,Method="CRPL")

R = 
2.7171e+04

SRtrue = 
2.7163e+04

elTrue = 
1.9666

Input Arguments

tgtht — Target height (m)

nonnegative scalar | nonnegative length-M row vector

Target height specified as a nonnegative scalar or length-M row vector. If tgtht is a vector, it must have the same size as the other vector input arguments of height2range. Heights are referenced to the ground. Units are in meters.

Data Types: double

anht — Sensor height (m)

nonnegative scalar | nonnegative length-M row vector

Sensor height specified as a nonnegative scalar or length-M row vector. If anht is a vector, it must have the same size as the other vector input arguments of height2range. Heights are referenced to the ground. Units are in meters.

Data Types: double

el — Sensor elevation angle (deg)

real-valued scalar | length-M row vector

Elevation angle of the sensor, specified as scalar or length-M row vector. The elevation angle is the initial elevation angle of the ray leaving the sensor. If el is a vector, it must have the same size as the other vector input arguments of height2range. Units are in degrees.

Data Types: double

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Example: r = height2range(tgtht,anht,el,Method="CRPL",SurfaceRefractivity=300,RefractionExponent=0.15)

Method — Earth model

"Curved" | "Flat" | "CRPL"

Earth model used for the computation, specified as "Curved", "Flat", or "CRPL".

• "Curved" — Assumes a Curved Earth Model with an effective radius of 4/3 times the actual Earth radius, which is a commonly used approximation for modeling refraction effects in the troposphere. To specify another value for the effective Earth radius, use the EffectiveEarthRadius name-value pair argument.

• "Flat" — Assumes a Flat Earth Model. In this case, the effective Earth radius is infinite.

• "CRPL" — Assumes a curved Earth model with the atmosphere defined by the CRPL Exponential Reference Atmosphere Model with a refractivity of 313 N-units and a refraction exponent of 0.143859 km^–1. To specify other values for the refractivity and the refraction exponent, use the SurfaceRefractivity and RefractionExponent name-value arguments. This CRPL Exponential model accounts for refraction at elevation angles greater than approximately 10 millirad (about 0.573 degrees) and heights above approximately 1 km. For more information, see CRPL Model Geometry.

Data Types: char | string

EffectiveEarthRadius — Effective Earth radius

4/3 of Earth's radius (default) | positive scalar

Effective Earth radius in meters, specified as a positive scalar. If this argument is not specified, height2range calculates the effective Earth radius using a refractivity gradient of –39 × 10^–9 N-units/meter, which results in approximately 4/3 of the real Earth radius. This argument applies only if Method is specified as "Curved".

Data Types: double

SurfaceRefractivity — Surface refractivity

313 (default) | real-valued scalar

Surface refractivity in N-units, specified as a nonnegative real-valued scalar. The surface refractivity is a parameter of the CRPL Exponential Reference Atmosphere Model used by height2range. This argument applies only if Method is specified as "CRPL".

Data Types: double

RefractionExponent — Refraction exponent

0.143859 (default) | real-valued scalar

Refraction exponent, specified as a nonnegative real-valued scalar. The refraction exponent is a parameter of the CRPL Exponential Reference Atmosphere Model used by height2range. This argument applies only if Method is specified as "CRPL".

Data Types: double

Output Arguments

r — Propagated range (m)

scalar | real-valued length-M row vector

Propagated range between the target and sensor, returned as a scalar or real-valued length-M row vector. If r is a vector, it has the same size as the vector input arguments of height2range. The propagated range is the distance along the slightly curved propagated path that results from atmospheric refraction over long distances and is the range that would be retrieved from measurements acquired by a sensor with pointing geometry defined by tgtht, anht, and el. Units are in meters.

Data Types: double

sr — Slant range (m)

scalar | length-M row vector

Slant range, or straight-line geometric distance between sensor and target, returned as a scalar or length-M real-valued row vector. Units are in meters.

Example: 5000.0

Data Types: double

t_el — Elevation angle

scalar | real-valued length-M row vector

Elevation angle between the target and propagated path r, returned as a scalar or real-valued length-M row vector.

Data Types: double

More About

Flat Earth Model

The flat Earth model assumes that the Earth has infinite radius and that the index of refraction of air is uniform throughout the atmosphere. The flat Earth model is applicable over short distances and is used in applications like communications, automotive radar, and synthetic aperture radar (SAR).

Given the antenna height h_a and the initial elevation angle θ₀, the model relates the target height h_T and the slant range R_T by

$$h_T=h_a+R_T\sin {\theta }_0\iff R_T=\left(h_T-h_a\right)\csc {\theta }_0,$$

so knowing one of those magnitudes enables you to compute the other. In this model, the propagated range is equivalent to the slant range, R_T, and the initial elevation angle θ₀ is considered to be the elevation angle between the target and the propagated path.

To compute the ground range G, use

$$G=\left(h_T-h_a\right)\cot {\theta }_0.$$

Curved Earth Model

Atmospheric refraction bends radar signals, which causes a slightly curved propagation path that is longer than the straight-line slant path to the target. In other words, over long distances, the propagated range is greater than the slant range due to refraction. The curved Earth model leverages the fact that the index of refraction of air depends on height and uses an effective Earth radius that is larger than the actual value to approximate the propagated path as a straight line. Therefore, in this model, the propagated range is the length of the slant range that is determined using a larger effective Earth radius.

Given the effective Earth radius R₀, the antenna height h_a, and the initial elevation angle θ₀, the model relates the target height h_T and the slant range R_T by

$${\left(R_0+h_T\right)}^2={\left(R_0+h_a\right)}^2+R_T^2+2R_T\left(R_0+h_a\right)\sin {\theta }_0.$$

In this equation, R_T approximates the propagated range because R₀ is larger than the actual Earth radius. Similarly, the initial elevation angle θ₀ is considered to be the elevation angle between the target and the propagated path.

The equation can be rearrange to solve for the target height,

$$h_T=\sqrt{{\left(R_0+h_a\right)}^2+R_T^2+2R_T\left(R_0+h_a\right)\sin {\theta }_0}-R_0.$$

To compute the ground range G, use

$$G=R_0\varphi =R_0\arcsin \frac{R_T\cos {\theta }_0}{R_0+h_T}.$$

A standard propagation model uses an effective Earth's radius that is 4/3 times the actual value. This model has two major limitations:

1. The model implies a value for the index of refraction near the Earth's surface that is valid only for certain areas and at certain times of the year. To mitigate this limitation, use an effective Earth's radius based on the near-surface refractivity value.

2. The model implies a value for the gradient of the index of refraction that is unrealistically low at heights of around 8 km. To partially mitigate this limitation, use an effective Earth's radius based on the platform altitudes.

For more information, see effearthradius.

CRPL Exponential Reference Atmosphere Model

Atmospheric refraction evidences itself as a deviation in an electromagnetic ray from a straight line due to variation in air density as a function of height. The Central Radio Propagation Laboratory (CRPL) exponential reference atmosphere model treats refraction effects by assuming that the index of refraction n(h) and the refractivity N decay exponentially with height. The model defines

$$N=\left(n\left(h\right)-1\right)\times {10}^6=N_{\text{s}}{e}^{-R_{\text{exp}}h},$$

where N_s is the atmospheric refractivity value (in units of 10^–6) at the surface of the earth, R_exp is the decay constant, and h is the height above the surface in kilometers. Thus

$$n(h)=1+\left(N_{\text{s}}\times {10}^{-6}\right)e^{-R_{\text{exp}}h}.$$

The default value of N_s is 313 N-units and can be modified using the SurfaceRefractivity name-value argument in functions that accept it. The default value of R_exp is 0.143859 km^–1 and can be modified using the RefractionExponent name-value argument in functions that accept it. This CRPL Exponential model accounts for refraction at elevation angles greater than approximately 10 millirad (about 0.573 degrees) and heights above approximately 1 km.

CRPL Model Geometry

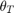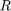When the refractivity of air is incorporated into the curved Earth model, the ray paths do not follow a straight line but curve downward. (This statement assumes standard atmospheric propagation and nonnegative elevation angles.) The true elevation angle is different from the initial . The actual range , which is the distance along the curved path , is different from the slant range .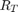

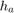Given the Earth's radius , the antenna height , the initial elevation angle , and the height-dependent index of refraction 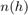with value at 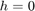, the modified model relates the target height 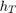and the actual range 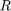by

When Method is specified as "CRPL", the integral is solved using 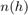from CRPL Exponential Reference Atmosphere Model.

To compute the ground range 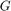, use

References

[1] Barton, David K. Radar Equations for Modern Radar. Norwood, MA: Artech House, 2013.

[2] Bean, B.R., and G.D. Thayer. "Central Radio Propagation Laboratory Exponential Reference Atmosphere." Journal of Research of the National Bureau of Standards, Section D: Radio Propagation 63D, no. 3 (November 1959): 315. https://doi.org/10.6028/jres.063D.031.

[3] Blake, Lamont V. "Ray Height Computation for a Continuous Nonlinear Atmospheric Refractive-Index Profile." Radio Science 3, no. 1 (January 1968): 85–92. https://doi.org/10.1002/rds19683185.

[4] Doerry, A. W. "Earth Curvature and Atmospheric Refraction Effects on Radar Signal Propagation." Sandia National Laboratories, SAND2012-10690 (Jan. 2013).

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.

Version History

Introduced in R2021b