CSTR Model
The adiabatic continuous stirred tank reactor (CSTR) is a common chemical system in the process industry, and it is described extensively in [1]. A single first-order exothermic and irreversible reaction, A → B, takes place in the vessel, which is assumed to be always perfectly mixed. The inlet stream of reagent A enters the tank at a constant volumetric rate. The product stream B exits continuously at the same volumetric rate, and liquid density is constant. Thus, the volume of reacting liquid is constant. The following figure shows a schematic diagram of the vessel and the surrounding cooling jacket.
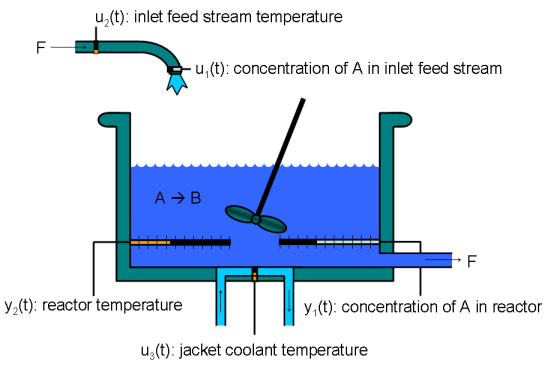
The inputs of the CSTR model are arranged in the vector u(t) and are as follows.
u1 — CAf, the concentration of reagent A in the inlet feed stream, measured in kmol/m3
u2 — Tf, the temperature of the inlet feed stream, measured in K
u3 — Tc, the temperature of the jacket coolant, measured in K
The first two inputs (concentration and temperature of the inlet reagent feed stream, sometimes also indicated as CAi and Ti, respectively) are normally assumed to be constant unmeasured disturbances, while the third (temperature of the coolant) is the control input used to control the process. Note that the diagram is a simplified sketch; in reality the coolant flow surrounds the whole reactor jacket, and not just the bottom of it.
The states of the model are arranged in the vector x(t).
x1 — CA, the concentration of reagent A in the reactor, measured in kmol/m3
x2 — T, the temperature in the reactor, measured in K
Nonlinear Model
The CSTR system is modeled using basic mass balance and energy conservation principles. The change of the concentration of reagent A in the vessel per time unit can be modeled as follows.
The first term, where V is the reactor volume and F is the volumetric flow rate, expresses the concentration difference between the inlet and the stream. The second term is the reaction rate per unit of volume, and it is described by the Arrhenius rate law, as follows.
Here:
E is the activation energy.
R is the Boltzmann ideal gas constant.
T is the temperature in the reactor.
k0 is an unknown nonthermal constant.
The rate law states that the reaction rate increases exponentially with the absolute temperature.
Similarly, using the energy balance principle, and assuming constant volume in the reactor, the temperature change per unit of time can be modeled as follows.
Here, the first and third terms describe changes due to the inlet feed stream temperature Tf and jacket coolant temperature Tc, respectively. The second term represents the influence on the reactor temperature caused by the chemical reaction in the vessel.
In this equation:
ΔH is the heat of the reaction, per mole.
Cp is a heat capacity coefficient.
ρ is a density coefficient.
U is an overall heat transfer coefficient.
A is the area for the heat exchange (coolant/vessel interface area).
A Simulink® representation of this nonlinear reactor model is available in the models
CSTR_OpenLoop and CSTR_INOUT. It is used in several
examples illustrating how to linearize nonlinear models and how to use linear, adaptive,
gain-scheduled, and nonlinear MPC to control a nonlinear plant.
Parameters of the Nonlinear CSTR Simulink Model
| Parameter | Value | Unit | Description |
|---|---|---|---|
| F | 1 | m3/h | Volumetric flow rate |
| V | 1 | m3 | Reactor volume |
| R | 1.985875 | kcal/(kmol·K) | Boltzmann's ideal gas constant |
| ΔH | -5,960 | kcal/kmol | Heat of reaction per mole |
| E | 11,843 | kcal/kmol | Activation energy per mole |
| k0 | 34,930,800 | 1/h | Pre-exponential nonthermal factor |
| ρCp | 500 | kcal/(m3·K) | Density multiplied by heat capacity |
| UA | 150 | kcal/(K·h) | Overall heat transfer coefficient multiplied by tank area |
In the model, the initial value of CA is 8.5698 kmol/m3 and the initial value for T is 311.2639 K. This operating point is an equilibrium when the inflow feed concentration CAf is 10 kmol/m3, the inflow feed temperature Tf is 300 K, and the coolant temperature Tc is 292 K.
In the example Non-Adiabatic Continuous Stirred Tank Reactor: MATLAB File Modeling with Simulations in Simulink (System Identification Toolbox), you use the above equations to estimate the last four parameters when the disturbance inputs CAf and Tf stay around to 10 kmol/m3 and 298 K, respectively, and the control input Tc ranges from 273 to 322 K. The first state variable, CA, ranges from 0 to 10 kmol/m3 and the second one, T, ranges from 310 to 390 K. The values of the last four parameters are estimated to be 11,854, 35,588,869, 500.7095, and 150.1275, respectively, with the same units as in the table.
Linear Model
A linearized model of the CSTR, in which Tf does not deviate from its nominal condition, can be represented by the following linear differential equations.
Here, the primes (for example, C′A) denote a deviation from the nominal steady-state condition at which the model has been linearized. The constants aij and bij are the coefficients of the Jacobian matrices (normally indicated as A and B) with respect to state and input, respectively. A symbolic expression of the majority of these coefficients is given in [1].
Since measurement of reactant concentrations is often difficult, a common assumption is that T is the only measured output, while CA is unmeasured. For similar reasons, CAf is commonly assumed to be an unmeasured disturbance. In general, Tc, is the manipulated variable used to control the reactor.
The linearized model fits the general state-space format
where
The following code shows how to define such a model for some specific values of the aij and bij constants:
A = [ -5 -0.3427;
47.68 2.785];
B = [ 0 1
0.3 0];
C = flipud(eye(2));
D = zeros(2);
CSTR = ss(A,B,C,D);
These values correspond to a linearization around an operating point in which CA is 2 kmol/m3, T is 373 K, CAf is 10 kmol/m3, Tf is 300 K, and Tc is 299 K. See Linearization Using MATLAB Code for more information.
You can specify the input, output, and state names for your CSTR model. Also, you can specify the input and output signals types.
CSTR.InputName = {'T_c', 'C_A_f'}; % set names of input signals
CSTR.OutputName = {'T', 'C_A'}; % set names of output signals
CSTR.StateName = {'C_A', 'T'}; % set names of state variables
% assign input and output signals to different MPC categories
CSTR=setmpcsignals(CSTR,'MV',1,'UD',2,'MO',1,'UO',2);Here, MV, UD, MO, and
UO stand for "Manipulated Variable," "Unmeasured Disturbance,"
"Measured Output," and "Unmeasured Output," respectively.
View the CSTR model and its properties.
CSTR
CSTR =
A =
C_A T
C_A -5 -0.3427
T 47.68 2.785
B =
T_c C_A_f
C_A 0 1
T 0.3 0
C =
C_A T
T 0 1
C_A 1 0
D =
T_c C_A_f
T 0 0
C_A 0 0
Input groups:
Name Channels
Manipulated 1
Unmeasured 2
Output groups:
Name Channels
Measured 1
Unmeasured 2
Continuous-time state-space model.In summary, in this linearized model, the first two state variables are the concentration of reagent and the temperature of the reactor, while the first two inputs are the coolant temperature and the inflow feed reagent concentration.
For details on how to obtain this linear model, see the two examples in Linearize Simulink Models. In the first example the linearization is done in MATLAB®, while in the second one it is done using Model Linearizer (Simulink Control Design) in Simulink.
Examples Using a CSTR model
The following examples use the linear CSTR model.
Construct Linear Time Invariant Models – Create LTI state-space models for MPC design using the linear CSTR model.
Design Controller Using MPC Designer – Use a linear CSTR model where the reactor temperature is a measured output. Using MPC Designer, you design an MPC controller that stabilizes the closed-loop while constraining the CSTR coolant temperature and its rate of change.
Design MPC Controller at the Command Line – Design the same controller designed in the previous example but using MATLAB instructions.
Test MPC Controller Robustness Using MPC Designer – Test the sensitivity of your MPC controller to prediction errors using simulations in MPC Designer.
Compute Steady-State Output Sensitivity Gain – Analyze the steady-state performance of an MPC controller.
Compare Multiple Controller Responses Using MPC Designer – Compare multiple controller responses using MPC Designer.
The following examples use the nonlinear CSTR model.
The example Linearize Simulink Models Using MPC Designer shows how to linearize the nonlinear Simulink model of the reactor at different operating points, and using different approaches, in the context of designing an MPC controller, using MPC Designer.
Similarly, in the example Design MPC Controller in Simulink, the MPC Designer is used first to linearize the same
nonlinear model around an operating point in which
CA is around 2
(kg·mol)/m3 and then to design an MPC controller for the
linearized plant. In this example CA is the only
measured output (and Tc is the control
input).
The example Simulate Linear MPC Controller with Nonlinear Plant Using Successive Linearizations uses a for loop to successively
linearize the nonlinear model using the linmod command, redesign a linear
MPC controller, calculate the control input, and feed it back into the nonlinear Simulink model at each time step. This approach is no longer recommended, use Adaptive and Time-Varying MPC or Gain-Scheduled MPC
instead.
The example Adaptive MPC Control of Nonlinear Chemical Reactor Using Successive Linearization uses the Adaptive MPC Controller block to simulate the closed-loop directly in Simulink. Here a linearization block is used to extract a linear plant model from the nonlinear equations at each time step. In general MPC adaptive control is the preferred approach when a linear plant model can be obtained at run time and when all the linearized plant models have the same order and time delay.
Similarly, in the example Adaptive MPC Control of Nonlinear Chemical Reactor Using Online Model Estimation a Recursive Polynomial Model Estimator is used (instead of a linearization block) to identify a two-input (Tf and Tc) and one-output (T) discrete time ARX model based on the measured temperatures at each control interval. The estimated model is then converted into state space and fed to an Adaptive MPC Controller block, which provides the control input to the nonlinear plant. Online estimation can be a good approach when the plant is stable and slowly varying, and its equations are not accurately known.
In the example Adaptive MPC Control of Nonlinear Chemical Reactor Using Linear Parameter-Varying System a linear parameter varying (LPV) system consisting of three linear plant models (at an initial, intermediate, and final operating point) is constructed offline. At run time, the LPV System block feeds an appropriate interpolation to an Adaptive MPC Controller block, which provides the control input to the nonlinear plant. Plant interpolation can be a good approach when, at a given point, the interpolated plant is a good approximation of the actual one, the scheduling variable varies comparatively slowly, and obtaining a linearized plant at run time might be too computationally expensive or unsafe.
In the example Gain-Scheduled MPC Control of Nonlinear Chemical Reactor three different MPC controllers (for the plant at an initial, intermediate, and final operating point) are designed. These controllers are stored in the Multiple MPC Controllers block and are switched at run time at appropriate points along the transition path. Switching controllers is a good approach when the linearized plant models have different order or time delays.
Finally, in the example Nonlinear Model Predictive Control of Exothermic Chemical Reactor, the nonlinear plant is controlled by a single Nonlinear MPC Controller block, using Tc as the control input and CA as the only measured output. In general, nonlinear MPC control is the remaining strategy to control highly nonlinear plants when all the previous approaches are unsuitable, or you need to use nonlinear constraints or non-quadratic cost functions.
References
[1] Bequette, B., Process Dynamics: Modeling, Analysis and Simulation, Prentice-Hall, 1998, Module 8, pp. 641-660.
[2] Seborg, D. E., T. F. Edgar, and D. A. Mellichamp, Process Dynamics and Control, 2nd Edition, Wiley, 2004, pp. 34–36 and 94–95.