reducepoly
Reduce density of points in ROI using Ramer–Douglas–Peucker algorithm
Description
Examples
Input Arguments
Output Arguments
Algorithms
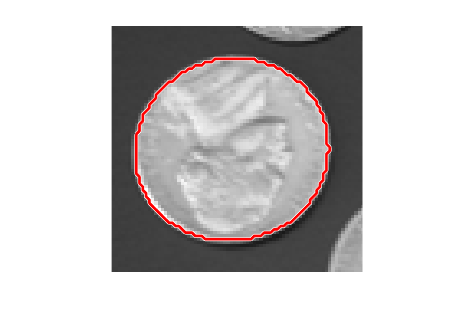
The Ramer-Douglas-Peucker line simplification algorithm recursively subdivides a shape
looking to replace a run of points with a straight line. The algorithm checks that no point in
the run deviates from the straight line by more than the value specified by
tolerance.
Version History
Introduced in R2019b
See Also
drawfreehand | drawpolygon | drawpolyline | drawassisted | bwboundaries