Using idnlarx as a Modern Alternative to narxnet

This example shows how to generate a NARX network using the idnlarx function from System Identification Toolbox™. To train a neural network for nonlinear systems, you can use the procedure described in this example to replace the use of the narxnet (Deep Learning Toolbox) function from Deep Learning Toolbox™ with idnlarx.

About NARX Networks

A NARX (Nonlinear AutoRegressive with eXogenous inputs) Network is a neural network that can learn to predict one time series given past values of the same time series, the feedback input, and possibly an auxiliary time series called the external (or exogenous) time series. It represents a prediction equation of the following form:

$$y(t)=f(y(t-1),y(t-2),\dots ,y(t-na),u(t-1),u(t-2),\dots ,u(t-nb)$$

The value of the dependent output signal $$y(t)$$ is regressed on previous values of the output signal and previous values of an independent (exogenous) input signal $$u(t)$$. A finite number of lagged values of the output and any inputs are used, denoted by $$na$$ and $$nb$$ in the equation. $$y(t)$$ and $$u(t)$$ can be multi-dimensional. This includes the situation where there are no exogeneous inputs (that is, there is no $$u(t)$$ input available). The corresponding model is a purely nonlinear autoregressive model (NAR).

The function $$f(\cdot )$$ is represented by a multi-layer feedforward neural network. For example, if the network has two layers, it takes the following form:

There are many applications for the NARX network. You can use it as a predictor, to predict the next value of the input signal. You can also use it for nonlinear filtering, in which the target output is a noise-free version of the input signal. You can use it in a black-box modeling approach for nonlinear dynamic systems.

In the Deep Learning Toolbox, you can create NARX networks using the narxnet (Deep Learning Toolbox) command. The resulting network is represented by the network object.

Alternatively, use the idnlarx model structure and the corresponding training command nlarx from System Identification Toolbox.

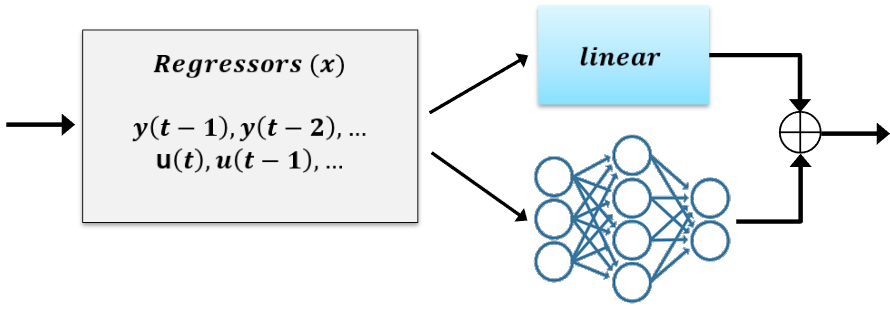
Transitioning from narxnet to idnlarx

The narxnet (Deep Learning Toolbox) command originated in the historical shallow networks and employs a terminology that is different from the modern one used in System Identification Toolbox. This example first establishes the equivalence between the concepts and terminology used in both these areas.

Open-Loop Models vs Closed-Loop Models

narxnet and idnlarx can represent two architectures - Parallel Architecture and Series Architecture.

You represent the parallel and the series-parallel models by different network objects in Deep Learning Toolbox. However, a single idnlarx model from System Identification Toolbox can serve both architectures. Depending on the application needs, you can run the idnlarx model in open-loop (series-parallel) or closed-loop (parallel) configurations.

Parallel Architecture

In the parallel case, the past output signal values used by the network (the terms $$y(t-1),y(t-2),\dots$$ in the network equation) are estimated by the network itself at previous time steps. This is also called a recurrent or a closed-loop model.

Closed-Loop narxnet Training and Simulation

Create an initial model using the narxnet (Deep Learning Toolbox) command. To create a parallel (closed-loop) configuration, specify FeedbackMode to be 'closed'.

model = narxnet(inputDelays,feedbackDelays,hiddenSizes,'closed')
view(model)

The model is a closed-loop network represented by the network object. Train the parameters (weights and biases) of the model using the train (Deep Learning Toolbox) command.

model_closedloop = train(model,input_data,output_data, ...)

You can compute the output of the trained model by using the sim method of the network object.

Closed-Loop idnlarx Training and Simulation

You can create an initial model using the idnlarx command without specifying the feedback mode. You specify the feedback mode during training as a value of the Focus training option.

net = idNeuralNetwork(hiddenSizes)
model = idnlarx([na nb nk],net)

Train the parameters (weights and biases) of the model using the nlarx command. Set the training focus to "simulation" using the nlarxOptions option set.

trainingOptions = nlarxOptions(Focus="simulation");
model = nlarx(input_data,output_data,model,trainingOptions)

In most situations, you can directly create the model by providing the orders and model structure information to the nlarx command, without first using idnlarx.

net = idNeuralNetwork(hiddenSizes)
model = nlarx(input_data,output_data,[na nb nk],net,trainingOptions)

The model is a nonlinear ARX model represented by the idnlarx object. You can compute the output of the trained model by using the sim method of the idnlarx object.

Series-Parallel Architecture

In the series-parallel case, the past output signal values used by the network (the terms $$y(t-1),y(t-2),\dots$$ in the network equation) are provided externally as measured values of the output signals. This is also called feedforward or an open-loop model.

Open-Loop narxnet Training and Simulation

Create an initial model using the narxnet (Deep Learning Toolbox) command. To create a series-parallel (open-loop) configuration, specify FeedbackMode to be 'open' (default value).

model = narxnet(inputDelays,feedbackDelays,hiddenSizes)

or

model = narxnet(inputDelays,feedbackDelays,hiddenSizes,'open')
view(model)

The model is an open-loop network represented by the network object. Train the parameters (weights and biases) of the model using the train (Deep Learning Toolbox) command.

model_openloop = train(model,input_data,output_data, ...)

You can compute the output of the trained model by using the sim method of the network object.

Open-Loop idnlarx Training and Simulation

As in the closed-loop case, you can create an initial model using the idnlarx command without specifying the feedback mode. You specify the feedback mode during training as a value of the Focus training option.

net = idNeuralNetwork(hiddenSizes)
model = idnlarx([na nb nk],net)

Train the parameters (weights and biases) of the model using the nlarx command. Set the training focus to "prediction" (default value) using the nlarxOptions option set.

trainingOptions = nlarxOptions(Focus="prediction");
model = nlarx(data,model,trainingOptions)

In most situations, you can directly train the model by providing the orders and model structure information to the nlarx command.

net = idNeuralNetwork(hiddenSizes)
model = nlarx(data,[na nb nk],net,trainingOptions)

The model is a nonlinear ARX model represented by the idnlarx object. Structurally, it is the same as the closed-loop model. Therefore, you require different commands to compute the open-loop and closed-loop simulation results. As described earlier, you compute the closed-loop simulation using the sim command. For open-loop results, use the predict command with a prediction horizon of one.

y = predict(model,past_data,1)   % open-loop simulation

You can also use the predict command for obtaining the closed-loop simulation results by using a prediction horizon of Inf.

y = predict(model,past_data,Inf) % closed-loop simulation

When using narxnet, the closed-loop model (parallel) is structurally different from the open-loop one (series-parallel). It is possible to use an open-loop network for closed-loop simulations, but that requires an explicit conversion of the open-loop network into a closed-loop one. This is achieved using the closeloop (Deep Learning Toolbox) command.

[model_closedloop,Xic,Aic] = closeloop(model_openloop,Xf,Af);

When using nlarx, no such conversion is required since the open-loop trained model is structurally identical to the closed-loop trained one. Instead, you choose between the sim and predict commands, as shown above.

Data Format

narxnet training requires the input and output time series (signals) to be provided as cell arrays. Each element of the cell array represents one observation at a given time instant. For multivariate signals, each cell element must contain as many rows as there are variables. Suppose the training data for a process with one output and two inputs is as following:

Time (t)	Input 1 (u1)	Input 2 (u2)	Output (y)
0	1	5	100
0.1	2	-2	500
0.2	0	4	-100
0.3	10	34	-200

The format of the input data for narxnet (Deep Learning Toolbox) must be:

% input data
u = {[1; 5], [2; -2], [0; 4], [10; 34]};
% output data
y = {100, 500, -100, -200};

Furthermore, this data must be shifted for various lag values (na, nb) explicitly before using for training.

na = 2; 
nb = 3; % u1(t-1), u1(t-2), u1(t-3), u2(t-1), u2(t-2), u3(t-3) 
net = narxnet(1:nb,1:na, 10);
[u_shifted,u_delay_states, layer_delay_states, y_shifted] = preparets(net,u,{},y)

u_shifted=2×1 cell array
    {2×1 double}
    {[    -200]}

u_delay_states=2×3 cell array
    {2×1 double}    {2×1 double}    {2×1 double}
    {[     100]}    {[     500]}    {[    -100]}

layer_delay_states =

  2×0 empty cell array

y_shifted = 1×1 cell array
    {[-200]}

% Train the model
% net = train(net,u_shifted,y_shifted,u_delay_states,layer_delay_states);

In contrast, nlarx requires the data to be specified as double matrices with variables along the columns and the observations along the rows. These can be a pair of double matrices, a timetable, or an iddata object.

% input data
u1 = [1 2 0 10]';
u2 = [5 -2 4 34]';
u = [u1, u2];
% output data
y = [100, 500, -100, -200]';
% training
% model = nlarx(u, y, network_structure)

Alternatively, use a timetable for data (recommended syntax). The benefit of using a timetable is that the knowledge of the time vector is retained and carried over to the model. You can also specify the names of the input variables, if needed.

target = seconds(0:0.1:0.3)';
TT = timetable(target,u1,u2,y)

TT=4×3 timetable
    target     u1    u2     y  
    _______    __    __    ____

    0 sec       1     5     100
    0.1 sec     2    -2     500
    0.2 sec     0     4    -100
    0.3 sec    10    34    -200

% training
% model = nlarx(TT, [na nb nk], network_structure)

Similarly, you can replace a timetable with an iddata object.

DAT = iddata(y, u, 0.1, Tstart=0);
% training
% model = nlarx(DAT, [na, nb, nk], network_structure) 

Specifying Model Orders

The narxnet (Deep Learning Toolbox) function requires you to specify the lags to use for the input and output variables. In the multi-output case (that is, the number of output variables > 1), the lags used for all output variables must match. Similarly, the lags used for the input variables must all match.

input_lags = 0:3;
output_lags = 1:2;
hiddenLayerSizes = [10 5]; % two hidden layers
model = narxnet(input_lags,output_lags,hiddenLayerSizes);

You use the specified lags to generate the input features or predictors, also called regressors. For the above example, these regressors are: $$y(t-1)$$, $$y(t-2)$$, $$u_1(t)$$, $$u_1(t-1)$$, $$u_1(t-2)$$, $$u_1(t-3)$$, $$u_2(t)$$, $$u_2(t-1)$$, $$u_2(t-2)$$, $$u_2(t-3)$$, where $$y(t)$$ denotes the output signal, and $$u_1(t),u_2(t)$$ denote the two input signals. In the system identification terminology, these are called linear regressors.

When using the idnlarx framework, you create the linear, consecutive-lag regressors by specifying the maximum lag in each output (na), the minimum (nk), and the total number of input variable lags (nb). You put these numbers together in a single order matrix. You can pick different lags for different input and output variables.

na = 2;     % output lags
nb = [4 2]; % total number of consecutive lags in the two inputs
nk = [0 5]; % minimum lags in the two inputs
hiddenLayerSizes = [10 5]; % 2 hidden layers
netfcn = idNeuralNetwork(hiddenLayerSizes, NetworkType="dlnetwork");
model = idnlarx("y", ["u1", "u2"], [na nb nk], netfcn)

model =

Nonlinear ARX model with 1 output and 2 inputs
  Inputs: u1, u2
  Outputs: y

Regressors:
  Linear regressors in variables y, u1, u2
  List of all regressors

Output function: Deep learning network
Sample time: 1 seconds

Status:                                                         
Created by direct construction or transformation. Not estimated.

Model Properties

The choice of the above lags results in creation of the following regressors, whose formulas can be generated programmatically.

getreg(model)

ans = 8×1 cell
    {'y(t-1)' }
    {'y(t-2)' }
    {'u1(t)'  }
    {'u1(t-1)'}
    {'u1(t-2)'}
    {'u1(t-3)'}
    {'u2(t-5)'}
    {'u2(t-6)'}

With idnlarx models, you can incorporate more complex form of regressors, such as $$|y(t-1)|$$, $$y(t-2)u(t-5)$$, $$u^3(t)$$, $$sin(2\pi \cdot u(t-1))$$, and so on. To do this, use the dedicated regressor creator functions: linearRegressor, polynomialRegressor, periodicRegressor, and customRegressor. Some examples are:

vars = ["y", "u1", "u2"];
% Absolute valued regressors
UseAbs = true;
R1 = linearRegressor(vars(1:2), 1:2, UseAbs) % generate absolute value regressors for y and u1

R1 = 
Linear regressors in variables y, u1
       Variables: {'y'  'u1'}
            Lags: {[1 2]  [1 2]}
     UseAbsolute: [1 1]
    TimeVariable: 't'

  Regressors described by this set

getreg(R1)

ans = 4×1 string
    "|y(t-1)|"
    "|y(t-2)|"
    "|u1(t-1)|"
    "|u1(t-2)|"

% Second order polynomial regressors with different lags for each variable
UseAbs = false;
UseLagMix = true;
R2 = polynomialRegressor(vars,{[1 2],0, [4 9]},2,UseAbs,false,UseLagMix)

R2 = 
Order 2 regressors in variables y, u1, u2
               Order: 2
           Variables: {'y'  'u1'  'u2'}
                Lags: {[1 2]  [0]  [4 9]}
         UseAbsolute: [0 0 0]
    AllowVariableMix: 0
         AllowLagMix: 1
        TimeVariable: 't'

  Regressors described by this set

getreg(R2)

ans = 7×1 string
    "y(t-1)^2"
    "y(t-2)^2"
    "y(t-1)*y(t-2)"
    "u1(t)^2"
    "u2(t-4)^2"
    "u2(t-9)^2"
    "u2(t-4)*u2(t-9)"

% Periodic regressors in "u2" with lags 0, 4
% Generate three Fourier terms with a fundamental frequency of pi. Generate both sine and cosine functions.
R3 = periodicRegressor(vars(3), [0 4], pi, 3)

R3 = 
Periodic regressors in variables u2 with 3 Fourier terms
       Variables: {'u2'}
            Lags: {[0 4]}
               W: 3.1416
        NumTerms: 3
          UseSin: 1
          UseCos: 1
    TimeVariable: 't'
     UseAbsolute: 0

  Regressors described by this set

getreg(R3)

ans = 12×1 string
    "sin(3.142*u2(t))"
    "sin(2*3.142*u2(t))"
    "sin(3*3.142*u2(t))"
    "cos(3.142*u2(t))"
    "cos(2*3.142*u2(t))"
    "cos(3*3.142*u2(t))"
    "sin(3.142*u2(t-4))"
    "sin(2*3.142*u2(t-4))"
    "sin(3*3.142*u2(t-4))"
    "cos(3.142*u2(t-4))"
    "cos(2*3.142*u2(t-4))"
    "cos(3*3.142*u2(t-4))"

You can replace the orders matrix with a vector of regressors in the idnlarx or the nlarx command.

Regressors = [R1 R2 R3];
model = idnlarx("y", ["u1", "u2"], Regressors, netfcn);
getreg(model)

ans = 23×1 cell
    {'|y(t-1)|'            }
    {'|y(t-2)|'            }
    {'|u1(t-1)|'           }
    {'|u1(t-2)|'           }
    {'y(t-1)^2'            }
    {'y(t-2)^2'            }
    {'y(t-1)*y(t-2)'       }
    {'u1(t)^2'             }
    {'u2(t-4)^2'           }
    {'u2(t-9)^2'           }
    {'u2(t-4)*u2(t-9)'     }
    {'sin(3.142*u2(t))'    }
    {'sin(2*3.142*u2(t))'  }
    {'sin(3*3.142*u2(t))'  }
    {'cos(3.142*u2(t))'    }
    {'cos(2*3.142*u2(t))'  }
    {'cos(3*3.142*u2(t))'  }
    {'sin(3.142*u2(t-4))'  }
    {'sin(2*3.142*u2(t-4))'}
    {'sin(3*3.142*u2(t-4))'}
    {'cos(3.142*u2(t-4))'  }
    {'cos(2*3.142*u2(t-4))'}
    {'cos(3*3.142*u2(t-4))'}

Network Structure Specification

The narxnet (Deep Learning Toolbox) command does not allow you to pick the type of activation functions used by each hidden layer. The tanh activation function is used in all the layers. In contrast, you can create idnlarx networks that use a variety of different activation functions.You can also use custom networks, for example, created using the Deep Network Designer app.

Example 1: Train a Simple NARX Network and Predict on New Data

This example trains a nonlinear autoregressive with external input (NARX) neural network and compares its response to the test data output. For the comparison, simulate the trained (open-loop) model in closed-loop.

narxnet Approach

[X,T] = simpleseries_dataset;

Partition the data into training data XTrain and TTrain, and data for prediction XPredict. Use XPredict to perform prediction after you create the closed-loop network.

% training data
XTrain = X(1:80);
TTrain = T(1:80);

% test data
XPredict = X(81:100);
YPredict = T(81:100); 
rng default % for reproducibility of shown results

Create a NARX network. Define the input delays, feedback delays, and size of the hidden layer.

numUnits = 4;
model_narxnetOL = narxnet(1:2,1:2,numUnits);

Prepare training data.

[Xs,Xi,Ai,Ts] = preparets(model_narxnetOL,XTrain,{},TTrain);

Train the model.

model_narxnetOL = train(model_narxnetOL,Xs,Ts,Xi,Ai);
view(model_narxnetOL)

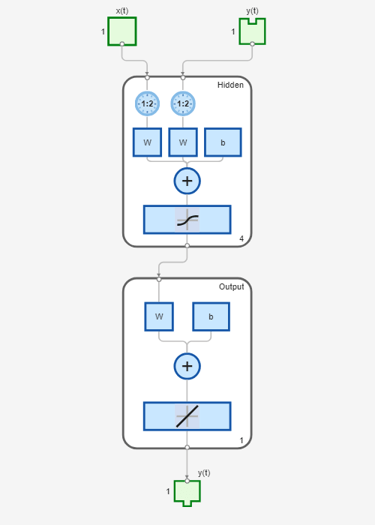
Simulate the model in closed-loop. Since model_narxnet is an open-loop model, first convert it into a closed-loop model.

[model_narxnetCL1,Xi_CL,Ai_CL] = closeloop(model_narxnetOL,Xi,Ai);
view(model_narxnetCL1) % notice the feedback loop

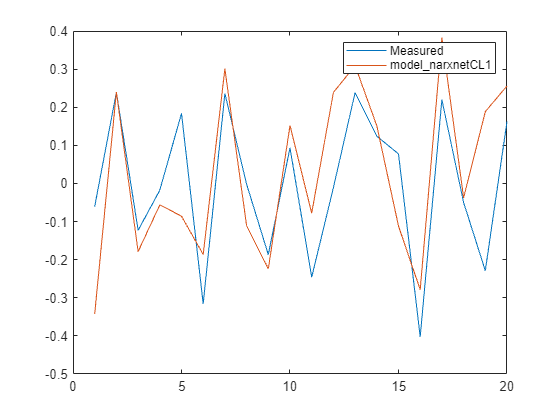
Ys1 = sim(model_narxnetCL1, XPredict, Xi_CL, Ai_CL);
Ys1 = cell2mat(Ys1)';
y_measured = cell2mat(YPredict)';
plot([y_measured,Ys1])
legend('Measured','model_narxnetCL1',Interpreter="none")

Now train the model in closed-loop (parallel architecture).

model_narxnetCL2 = narxnet(1:2,1:2,numUnits,'closed');
[Xs2,Xi2,Ai2,Ts2] = preparets(model_narxnetCL2,XTrain,{},TTrain);
model_narxnetCL2 = train(model_narxnetCL2,Xs2,Ts2,Xi2,Ai2);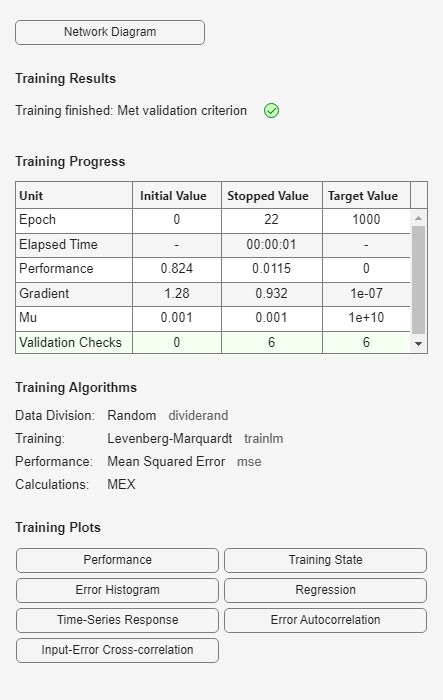

view(model_narxnetCL2)

The model model_narxnet_CL2 is already in a closed-loop configuration. So there is no need to call the closeloop (Deep Learning Toolbox) command on it.

Ys2 = sim(model_narxnetCL2, XPredict, Xi2, Ai2);
Ys2 = cell2mat(Ys2)';
plot([y_measured,Ys1,Ys2])
legend('Measured','model_narxnetCL1','model_narxnetCL2',Interpreter="none")

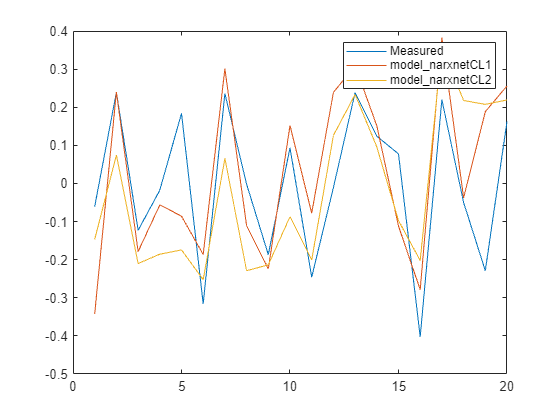
Measure the performance using NRMSE metric.

Err1 = goodnessOfFit(y_measured,Ys1,'nrmse')

Err1 = 
0.7679

Err2 = goodnessOfFit(y_measured,Ys2,'nrmse')

Err2 = 
0.9685

nlarx Approach

Prepare data.

% convert data to double vectors
% training data
XTrain = cell2mat(XTrain)'; 
TTrain = cell2mat(TTrain)';
% validation data
XPredict = cell2mat(XPredict)'; 
YPredict = cell2mat(YPredict)'; 

Prepare model orders.

na = 2;
nb = 2;
nk = 1;
Order = [na nb nk];

Create a network function that is similar to the one used by the narxnet models above. That is, create a network with one hidden tanh layer with 10 units. You can create the network by using the modern dlnetwork infrastructure from Deep Learning Toolbox, or the RegressionNeuralNetwork regression model from the Statistics and Machine Learning Toolbox™.

netfcn = idNeuralNetwork(numUnits, "tanh", NetworkType="RegressionNeuralNetwork");

The neural network function netfcn employs a parallel connection of a linear map with a network. This is useful for semi-physical modeling, where you have the option to initialize the linear piece using an existing, possibly physics-based, transfer function. However, for this example, turn off the use of the linear map so that the structure of netfcn is equivalent to the one used by narxnet models.

netfcn.LinearFcn.Use = false;

Identify an nlarx model in open-loop. Use the LM training method.

Method = "lm";
opt = nlarxOptions(Focus="prediction",SearchMethod=Method);
model_nlarxOL = nlarx(XTrain, TTrain, Order, netfcn, opt)

model_nlarxOL =

Nonlinear ARX model with 1 output and 1 input
  Inputs: u1
  Outputs: y1

Regressors:
  Linear regressors in variables y1, u1
  List of all regressors

Output function: Regression neural network
Sample time: 1 seconds

Status:                                            
Estimated using NLARX on time domain data "XTrain".
Fit to estimation data: 42.88% (prediction focus)  
FPE: 0.02822, MSE: 0.01541                         

Model Properties

Now train a model in closed-loop.

opt = nlarxOptions(Focus="simulation", SearchMethod=Method);
model_nlarxCL = nlarx(XTrain, TTrain, Order, netfcn, opt) % takes longer to train

model_nlarxCL =

Nonlinear ARX model with 1 output and 1 input
  Inputs: u1
  Outputs: y1

Regressors:
  Linear regressors in variables y1, u1
  List of all regressors

Output function: Regression neural network
Sample time: 1 seconds

Status:                                            
Estimated using NLARX on time domain data "XTrain".
Fit to estimation data: 33.74% (simulation focus)  
FPE: 0.04162, MSE: 0.02073                         

Model Properties

Note that model_nlarxOL and model_nlarxCL are structurally similar and you can use either one for open-loop or close-loop evaluation.

Perform open-loop evaluation. In the system identification terminology, this exercise is called one-step-ahead prediction.

Horizon = 1; % prediction horizon
[yp1,ic1] = predict(XPredict,YPredict,model_nlarxOL,Horizon);
[yp2,ic2] = predict(XPredict,YPredict,model_nlarxCL,Horizon);
plot([y_measured,yp1,yp2])
legend('Measured','model_nlarxOL','model_nlarxCL',Interpreter="none")
title('One-step Ahead (open-loop) Prediction')

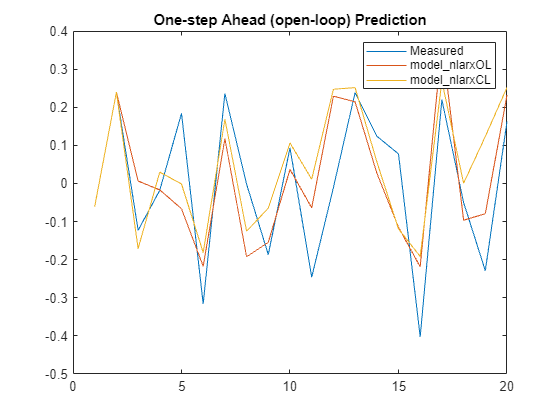
Measure the performance using NRMSE metric.

Err1 = goodnessOfFit(y_measured,yp1,'nrmse')

Err1 = 
0.8106

Err2 = goodnessOfFit(y_measured,yp2,'nrmse')

Err2 = 
0.9692

Perform closed-loop evaluation. In the system identification terminology, this exercise is called simulation or infinite-step-ahead prediction. You do not require the measured output (YPredict) for simulation.

ys1 = sim(model_nlarxOL,XPredict,simOptions(InitialCondition=ic1));
ys2 = sim(model_nlarxCL,XPredict,simOptions(InitialCondition=ic2));
plot([y_measured,ys1,ys2])
legend('Measured','model_nlarxOL','model_nlarxCL',Interpreter="none")
title('Closed-loop Prediction (Simulation)')

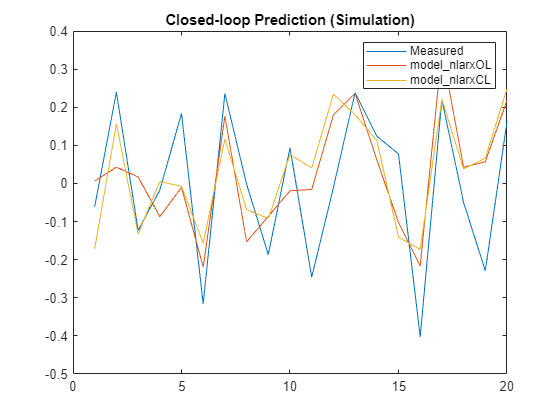
Measure the performance using NRMSE metric.

Err1 = goodnessOfFit(y_measured,ys1,'nrmse')

Err1 = 
1.0006

Err2 = goodnessOfFit(y_measured,ys2,'nrmse')

Err2 = 
1.0955

Example 2: Model the Dynamics of a Magnetic Levitation System

This example creates a NARX model of a magnetic levitation system using the position (output) and voltage (input) measurements. The data was collected at a sampling interval of 0.01 seconds.

[u,y] = maglev_dataset;
ud = cell2mat(u)';
yd = cell2mat(y)';
Ns = size(ud,1); % number of observations
time = seconds((0:Ns-1)*0.01)';
TT = timetable(time,ud,yd); % data represented by a timetable
stackedplot(TT)

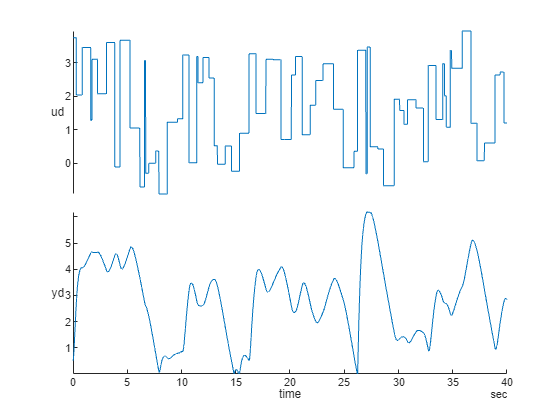
narxnet Approach

Create the series-parallel NARX network using narxnet (Deep Learning Toolbox). Use 10 neurons in the hidden layer and use the trainlm method for training.

rng default
d1 = 1:2;
d2 = 1:2;
numUnits = 10;
model_narxnet = narxnet(d1,d2,numUnits);
model_narxnet.divideFcn = '';
model_narxnet.trainParam.min_grad = 1e-10;
model_narxnet.trainParam.showWindow = false;
[p,Pi,Ai,target] = preparets(model_narxnet,u,{},y);

model_narxnet = train(model_narxnet,p,target,Pi);

Simulate the network and plot the resulting errors for the series-parallel implementation.

yp1 = sim(model_narxnet,p,Pi);
% convert to numerical vector with initial conditions appended
yp1 = [yd(1:2); cell2mat(yp1)'];

nlarx Approach

Create an idnlarx model that employs a one-hidden-layer network with 10 tanh units. Train the model using LM method, which is similar to the trainlm solver used by narxnet (Deep Learning Toolbox).

To use a neural network as a component of the nonlinear ARX model, use the idNeuralNetwork object. You can think of this object as a wrapper around a neural network which helps in its incorporation into the idnlarx model. idNeuralNetwork enables the use of networks from Deep Learning Toolbox (dlnetwork) and Statistics and Machine Learning Toolbox (RegressionNeuralNetwork).

rng default
UseLinear = false;
UseBias = false;
% Create a neural network object.
netfcn = idNeuralNetwork(10,"tanh",UseLinear,UseBias,NetworkType="dlnetwork");
OutputName = "yd";
InputName = "ud";
Reg = linearRegressor([OutputName, InputName],1:2);
model_nlarx = idnlarx(OutputName, InputName, Reg, netfcn);

opt = nlarxOptions(Focus="prediction",SearchMethod="lm");
opt.SearchOptions.MaxIterations = 15;
opt.SearchOptions.Tolerance = 1e-9;
opt.Display = "on";
opt.Normalize = false; % this is to match the default behavior of narxnet
model_nlarx = nlarx(TT, model_nlarx, opt)

model_nlarx =

Nonlinear ARX model with 1 output and 1 input
  Inputs: ud
  Outputs: yd

Regressors:
  Linear regressors in variables yd, ud
  List of all regressors

Output function: Deep learning network
Sample time: 0.01 seconds

Status:                                          
Estimated using NLARX on time domain data "TT".  
Fit to estimation data: 99.89% (prediction focus)
FPE: 2.491e-06, MSE: 2.415e-06                   

Model Properties

% predict (1-step-ahead) response.
yp2 = predict(model_nlarx,TT,1);

% compare the generated responses to the measured position data 
plot(time, yd, 'k.', time, yp1, time, yp2.yd);
legend('measured', 'narxnet', 'nlarx')
title('One-step Ahead (open-loop) Prediction')

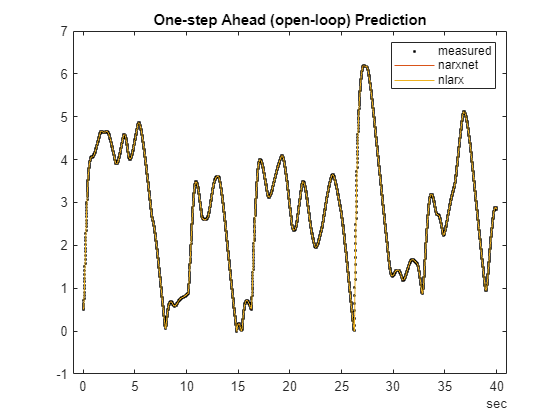
The plot indicates that both narxnet and nlarx methods predict the response perfectly, one-step ahead. Now assess their simulation (infinite-horizon prediction) abilities.

% Prepare validation (test) data
y1 = y(1700:2600);  yd1 = cell2mat(y1)';
u1 = u(1700:2600);  ud1 = cell2mat(u1)';
t = time(1700:2600);

% Simulate the narxnet model in closed loop
model_narxnetCL = closeloop(model_narxnet); % convert narxnet model into a recurrent model
[p1,Pi1,Ai1,t1] = preparets(model_narxnetCL,u1,{},y1);
ys1 = model_narxnetCL(p1,Pi1,Ai1);
ys1 = [yd1(1:2); cell2mat(ys1)'];

% Simulate the nlarx model. This can be done using sim command or using the predict command with a
% horizon of Inf. Here, you use predict.
ys2 = predict(model_nlarx, ud1, yd1, Inf);

% Plot the simulated response of the two models
plot(t, yd1, t, ys1, t, ys2) 
legend('measured', 'narxnet', 'nlarx')
title('Closed-loop Prediction (Simulation)')

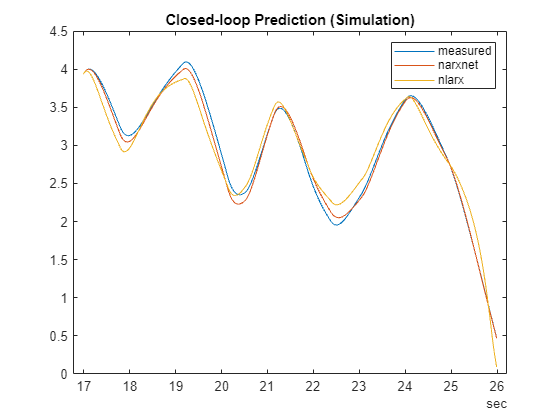
The simulation results match the measured data quite closely. You can retrieve the dlnetwork embedded in the trained model as follows:

fcn = model_nlarx.OutputFcn

fcn = 
Multi-Layer Neural Network
Inputs: yd(t-1), yd(t-2), ud(t-1), ud(t-2)
Output: yd(t)

 Nonlinear Function: Deep learning network
         Contains 1 hidden layers using "tanh" activations.
         (uses Deep Learning Toolbox)
 Linear Function: not in use
 Output Offset: not in use

              Network: 'Deep learning network parameters'
            LinearFcn: 'Linear function parameters'
               Offset: 'Offset parameters'
    EstimationOptions: [1×1 struct]

net = fcn.Network

net = 
Deep learning network parameters

    Parameters: 'Learnables and hyperparameters'
        Inputs: {'yd(t-1)'  'yd(t-2)'  'ud(t-1)'  'ud(t-2)'}
       Outputs: {'yd(t):Nonlinear'}

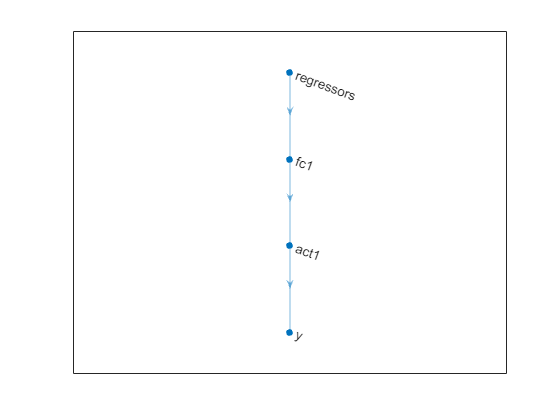
dlnet = getNetworkObj(net)

dlnet = 
  dlnetwork with properties:

         Layers: [4×1 nnet.cnn.layer.Layer]
    Connections: [3×2 table]
     Learnables: [4×3 table]
          State: [0×3 table]
     InputNames: {'regressors'}
    OutputNames: {'y'}
    Initialized: 1

  View summary with summary.

plot(dlnet)

Other Configurations of Nonlinear ARX Models

The idnlarx models afford a significantly larger flexibility in choosing an appropriate structure for the dynamics. In addition to the multi-layer neural networks (created using the idNeuralNetwork object), there are several other choices, such as:

1. idWaveletNetwork: Wavelet networks for describing multi-scale dynamics

2. idTreeEnsemble, idTreePartition: Regression trees and forests of such trees (boosted, bagged)

3. idGaussianProcess: Gaussian process regression maps

4. idSigmoidNetwork: Faster, one-hidden-layer neural networks using sigmoid activations

If you are going to employ a neural network with a single hidden layer, using idSigmoidNetwork or idWaveletNetwork is more efficient than using idNeuralNetwork. For example, create a sigmoid network based nonlinear ARX model for the magnetic levitation system.

netfcn = idSigmoidNetwork(10); % 10 units of sigmoid activations in one hidden layer
% train the model for the default open-loop performance (Focus = "prediction")
model_sigmoidOL = nlarx(ud(1:2000),yd(1:2000),[2 2 1],netfcn)

model_sigmoidOL =

Nonlinear ARX model with 1 output and 1 input
  Inputs: u1
  Outputs: y1

Regressors:
  Linear regressors in variables y1, u1
  List of all regressors

Output function: Sigmoid network with 10 units
Sample time: 1 seconds

Status:                                          
Estimated using NLARX on time domain data.       
Fit to estimation data: 99.94% (prediction focus)
FPE: 8.477e-07, MSE: 7.935e-07                   

Model Properties

% train the model for closed-loop performance (Focus = "simulation")
opt = nlarxOptions(Focus="simulation");
opt.SearchMethod = "lm";
opt.SearchOptions.MaxIterations = 40;
model_sigmoidCL = nlarx(ud(1:2000),yd(1:2000),[2 2 1],netfcn,opt)

model_sigmoidCL =

Nonlinear ARX model with 1 output and 1 input
  Inputs: u1
  Outputs: y1

Regressors:
  Linear regressors in variables y1, u1
  List of all regressors

Output function: Sigmoid network with 10 units
Sample time: 1 seconds

Status:                                          
Estimated using NLARX on time domain data.       
Fit to estimation data: 94.41% (simulation focus)
FPE: 5.597e-07, MSE: 0.006894                    

Model Properties

Compare the closed-loop responses of the two models to measured test data. Rather than using the sim or predict commands, use the compare command. This command produces a plot overlaying the model results on the measured values and shows the percent fit to the data using the NRMSE measure (Fit = (1-NRMSE)*100).

close(gcf)
compare(ud(2001:end),yd(2001:end),model_sigmoidOL,model_sigmoidCL)

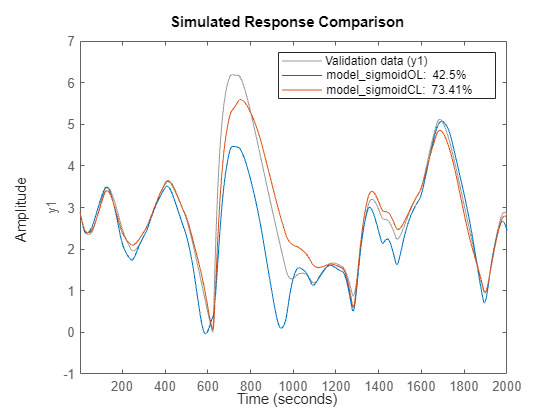
The plot shows the benefit of closed-loop training for predicting the response infinitely into the future.

Summary

narxnet can be replaced by nlarx. Some advantages of doing so are:

1. You can specify different lag indices for different input and/or output variables in case there are more than one inputs and/or outputs.

2. idnlarx allows the model regressors to be nonlinear functions of the lagged input/output variables.

3. You don't need to create separate open-loop and closed-loop variants of the trained model. The same model can be used for the open-loop and closed-loop evaluations.

4. idnlarx offers specialized forms for certain single-hidden-layer networks. Using them can speed up the training.

5. With idnlarx framework, you can leverage the state-of-the-art numerical solvers from Optimization Toolbox™ and Global Optimization Toolbox™. There are also several built-in line-search solvers available in System Identification Toolbox™ which have been calibrated for handling small to medium scale problems efficiently.

6. The idnlarx model structure allows physics-inspired learning. You can begin your modeling exercise with a simple linear model, which may have been derived by physical considerations or by using a linear model identification approach. You can then augment this linear model with a nonlinear function in order to improve its fidelity.

7. Using the idNeuralNetwork object, you can incorporate the deep networks created using Deep Learning Toolbox and a variety of regression models from Statistics and Machine Learning Toolbox.

8. You can use an idnlarx model for N-step-ahead prediction where N can vary from one to infinity. This can be extremely useful for assessing the time horizon over which the model is usable.