Identify Nonlinear Black-Box Models Using System Identification App
Introduction
Objectives
Estimate and validate nonlinear models from single-input/single-output (SISO) data to find the one that best represents your system dynamics.
After completing this tutorial, you will be able to accomplish the following tasks using the System Identification app:
Import data objects from the MATLAB® workspace into the app.
Estimate and validate nonlinear models from the data.
Plot and analyze the behavior of the nonlinearities.
Data Description
This tutorial uses the data file twotankdata.mat, which contains
SISO time-domain data for a two-tank system, shown in the following figure.
Two-Tank System

In the two-tank system, water pours through a pipe into Tank 1, drains into Tank 2, and leaves the system through a small hole at the bottom of Tank 2. The measured input u(t) to the system is the voltage applied to the pump that feeds the water into Tank 1 (in volts). The measured output y(t) is the height of the water in the lower tank (in meters).
Based on Bernoulli's law, which states that water flowing through a small hole at the bottom of a tank depends nonlinearly on the level of the water in the tank, you expect the relationship between the input and the output data to be nonlinear.
twotankdata.mat includes 3000 samples with a sample time of 0.2
s.
What Are Nonlinear Black-Box Models?
Types of Nonlinear Black-Box Models
You can estimate nonlinear discrete-time black-box models for both single-output and multiple-output time-domain data. You can choose from two types of nonlinear, black-box model structures:
Nonlinear ARX models
Hammerstein-Wiener models
Note
You can estimate Hammerstein-Wiener black-box models from input/output data only. These models do not support time-series data, where there is no input.
For more information on estimating nonlinear black-box models, see Nonlinear Model Identification.
What Is a Nonlinear ARX Model?
A nonlinear ARX model consists of model regressors and an output function. The output function contains one or more mapping objects, one for each model output. Each mapping object can include a linear and a nonlinear function that act on the model regressors to give the model output and a fixed offset for that output. This block diagram represents the structure of a single-output nonlinear ARX model in a simulation scenario.

The software computes the nonlinear ARX model output y in two stages:
It computes regressor values from the current and past input values and the past output data.
In the simplest case, regressors are delayed inputs and outputs, such as u(t–1) and y(t–3). These kind of regressors are called linear regressors. You specify linear regressors using the
linearRegressorobject. You can also specify linear regressors by using linear ARX model orders as an input argument. For more information, see Nonlinear ARX Model Orders and Delay. However, this second approach constrains your regressor set to linear regressors with consecutive delays. To create polynomial regressors, use thepolynomialRegressorobject. To create periodic regressors that contain the sine and cosine functions of delayed input and output variables, use theperiodicRegressorobject. You can also specify custom regressors, which are nonlinear functions of delayed inputs and outputs. For example, u(t–1)y(t–3) is a custom regressor that multiplies instances of input and output together. Specify custom regressors using thecustomRegressorobject.You can assign any of the regressors as inputs to the linear function block of the output function, the nonlinear function block, or both.
It maps the regressors to the model output using an output function block. The output function block can include multiple mapping objects, with each mapping object containing linear, nonlinear, and offset blocks in parallel. For example, consider the following equation:
Here, x is a vector of the regressors, and r is the mean of x. is the output of the linear function block. represents the output of the nonlinear function block. Q is a projection matrix that makes the calculations well-conditioned. d is a scalar offset that is added to the combined outputs of the linear and nonlinear blocks. The exact form of F(x) depends on your choice of output function. You can select from the available mapping objects, such as tree-partition networks, wavelet networks, and multilayer neural networks. You can also exclude either the linear or the nonlinear function block from the output function.
When estimating a nonlinear ARX model, the software computes the model parameter values, such as L, r, d, Q, and other parameters specifying g.
The resulting nonlinear ARX models are idnlarx objects that store all model data, including model regressors and
parameters of the output function. For more information about these objects, see Nonlinear Model Structures.
What Is a Hammerstein-Wiener Model?
This block diagram represents the structure of a Hammerstein-Wiener model:

Where,
f is a nonlinear function that transforms input data u(t) as w(t) = f(u(t)).
w(t), an internal variable, is the output of the Input Nonlinearity block and has the same dimension as u(t).
B/F is a linear transfer function that transforms w(t) as x(t) = (B/F)w(t).
x(t), an internal variable, is the output of the Linear block and has the same dimension as y(t).
B and F are similar to polynomials in a linear Output-Error model. For more information about Output-Error models, see What Are Polynomial Models?
For ny outputs and nu inputs, the linear block is a transfer function matrix containing entries:
where j =
1,2,...,nyand i =1,2,...,nu.h is a nonlinear function that maps the output of the linear block x(t) to the system output y(t) as y(t) = h(x(t)).
Because f acts on the input port of the linear block, this function is called the input nonlinearity. Similarly, because h acts on the output port of the linear block, this function is called the output nonlinearity. If your system contains several inputs and outputs, you must define the functions f and h for each input and output signal. You do not have to include both the input and the output nonlinearity in the model structure. When a model contains only the input nonlinearity f, it is called a Hammerstein model. Similarly, when the model contains only the output nonlinearity h, it is called a Wiener model.
The software computes the Hammerstein-Wiener model output y in three stages:
Compute w(t) = f(u(t)) from the input data.
w(t) is an input to the linear transfer function B/F.
The input nonlinearity is a static (memoryless) function, where the value of the output a given time t depends only on the input value at time t.
You can configure the input nonlinearity as a sigmoid network, wavelet network, saturation, dead zone, piecewise linear function, one-dimensional polynomial, or a custom network. You can also remove the input nonlinearity.
Compute the output of the linear block using w(t) and initial conditions: x(t) = (B/F)w(t).
You can configure the linear block by specifying the orders of numerator B and denominator F.
Compute the model output by transforming the output of the linear block x(t) using the nonlinear function h as y(t) = h(x(t)).
Similar to the input nonlinearity, the output nonlinearity is a static function. You can configure the output nonlinearity in the same way as the input nonlinearity. You can also remove the output nonlinearity, such that y(t) = x(t).
Resulting models are idnlhw objects
that store all model data, including model parameters and nonlinearity
estimators. For more information about these objects, see Nonlinear Model Structures.
Prepare Data
Load Data into the MATLAB Workspace
Load sample data in twotankdata.mat by typing the following command
in the MATLAB Command Window:
load twotankdata
This command loads the following two variables into the MATLAB Workspace panel:
uis the input data, which is the voltage applied to the pump that feeds the water into Tank 1 (in volts).yis the output data, which is the water height in Tank 2 (in meters).
Creating iddata Objects
System Identification Toolbox™ data objects encapsulate both data values and data properties into a single entity. You can use the System Identification Toolbox commands to conveniently manipulate these data objects as single entities.
You must have already loaded the sample data into the MATLAB workspace, as described in Load Data into the MATLAB Workspace.
Use the following commands to create two iddata data objects, ze and zv, where
ze contains data for model estimation and zv
contains data for model validation. Ts is the sample time.
Ts = 0.2; % Sample time is 0.2 sec z = iddata(y,u,Ts); % First 1000 samples used for estimation ze = z(1:1000); % Remaining samples used for validation zv = z(1001:3000);
To view the properties of the iddata object, use the get command. For example:
get(ze)
MATLAB software returns the following data properties and values:
Domain: 'Time'
Name: ''
OutputData: [1000x1 double]
y: 'Same as OutputData'
OutputName: {'y1'}
OutputUnit: {''}
InputData: [1000x1 double]
u: 'Same as InputData'
InputName: {'u1'}
InputUnit: {''}
Period: Inf
InterSample: 'zoh'
Ts: 0.2000
Tstart: 0.2000
SamplingInstants: [1000x1 double]
TimeUnit: 'seconds'
ExperimentName: 'Exp1'
Notes: {}
UserData: []To modify data properties, use dot notation. For example, to assign channel names and units that label plot axes, type the following syntax in the MATLAB Command Window:
% Set time units to minutes ze.TimeUnit = 'sec'; % Set names of input channels ze.InputName = 'Voltage'; % Set units for input variables ze.InputUnit = 'V'; % Set name of output channel ze.OutputName = 'Height'; % Set unit of output channel ze.OutputUnit = 'm'; % Set validation data properties zv.TimeUnit = 'sec'; zv.InputName = 'Voltage'; zv.InputUnit = 'V'; zv.OutputName = 'Height'; zv.OutputUnit = 'm';
To verify that the InputName property of ze is
changed, type the following command:
ze.inputname
Tip
Property names, such as InputName, are not case sensitive. You
can also abbreviate property names that start with Input or
Output by substituting u for
Input and y for Output in the
property name. For example, OutputUnit is equivalent to
yunit.
Start the System Identification App
To open the System Identification app, type the following command in the MATLAB Command Window:
systemIdentification
The default session name, Untitled, appears in the title
bar.

Import Data Objects into the System Identification App
You can import the data objects into the app from the MATLAB workspace.
You must have already created the data objects, as described in Creating iddata Objects, and opened the app, as described in Start the System Identification App.
To import data objects:
In the System Identification app, select Import data > Data object.

This action opens the Import Data dialog box.
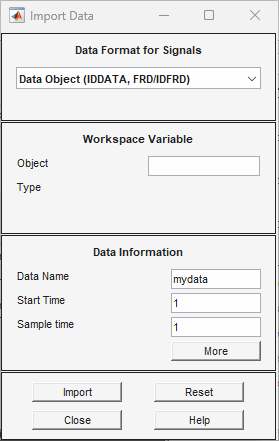
Enter
zein the Object field to import the estimation data. Press Enter.This action enters the object information into the Import Data fields.
Click More to view additional information about this data, including channel names and units.
Click Import to add the icon named
zeto the System Identification app.In the Import Data dialog box, type
zvin the Object field to import the validation data. Press Enter.Click Import to add the icon named
zvto the System Identification app.In the Import Data dialog box, click Close.
In the System Identification app, drag the validation data zv icon to the Validation Data rectangle. The estimation data ze icon is already designated in the Working Data rectangle.
Alternatively, right-click the
zvicon to open the Data/model Info dialog box. Select the Use as Validation Data check-box. Click Apply and then Close to addzvto the Validation Data rectangle.The System Identification app now resembles the following figure.

Estimate Nonlinear ARX Models
Estimate Nonlinear ARX Model with Default Settings
In this portion of the tutorial, you estimate a nonlinear ARX model using default model structure and estimation options.
You must have already prepared the data, as described in Prepare Data. For more information about nonlinear ARX models, see What Is a Nonlinear ARX Model?
Note
The illustrations in this tutorial represent a typical System Identification app session. Your results may not precisely match the results in the images.
In the System Identification app, select Estimate > Nonlinear ARX Models.

This action opens the Estimate Nonlinear ARX Models dialog box.

The dialog box contains two tabs — Model Structure and Estimation Options.
The Model Structure tab has the option to initialize using an existing model. It contains the parameters that configure the structure of the model, such as the choice of the regressors and the type of the output function. Specify the name of the model to be estimated in Model name. The default model name is
nlarx1.Use the Regressors tab to create the regressor sets to use. By default, the app creates a linear regressor set with lags
[1 2]in each variable and stores the regressor asLinear regressors #1in the Regressor Sets area. This panel contains a table that allows you to modify the lags to use for each variable.
The configuration panel Configure: Linear regressors #1 contains a table that shows the lag values that the regressor set uses. You can modify these lags.

The regressor assignment table Assign Regressors to Output Function lists the regressor names and the regressor assignments to the output function components.
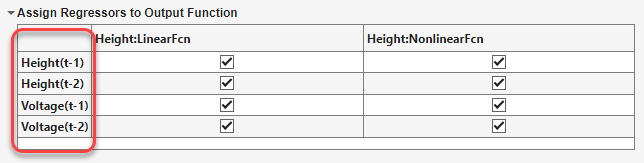
The regressor assignments in the table produce a model for the output
Heightof:Height(t) = f(Height(t-1), Height(t-2),Voltage(t-1),Voltage(t-2))
Here, f(.) is a static nonlinear function that maps the regressors to the output. To choose f(.) and its associated parameters, use the Output Function tab.
You can add more regressor sets, such as polynomials and custom formulas, by selecting a regressor type in Add regressors of type.

This example uses only
Linear regressors #1.Select the Output Function tab.
The tab shows that the app selects Wavelet Network as the default type of the output function f(.). This function uses a sum of a linear function, a nonlinear function (which is a sum of scaled wavelets), and an offset term to compute the output. The tab also shows a set of configuration parameters. The number of wavelets used by the function is configured to be chosen automatically during estimation. You can modify this selection. For the first estimate, keep the default choices.

Click Estimate.
This action adds the model
nlarx1to the model board of the System Identification app, as shown in the following figure.
Double click or right-click the model icon
nlarx1The model board shows information about the estimated model. The top area describes the model structure and estimation results (data used, percent fit and other quality metrics). The bottom area (Diary and Notes) shows the MATLAB script that you can use to reproduce the estimation results at the command line.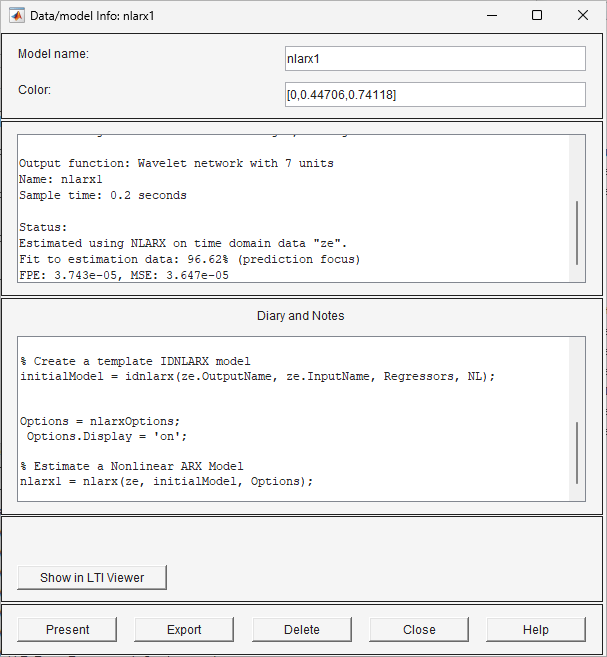
Note
Fit (%) is computed using the estimation data set with prediction focus, and not the validation data set. However, the model output plot in the next step compares the fit to the validation data set. To see how well the model can simulate the response of an independent validation dataset, use the Model Output plot, as discussed in the following step.
Select the model icon
nlarx1and in the Model Views area of the System Identification app, select Model output. This action simulates the model using the input validation data as the input to the model and plots the simulated output on top of the output validation data.
The Best Fits area of the model output plot shows the agreement between the model output and the validation-data output using a normalized root mean squared (NRMSE) metric of goodness of fit. The agreement is poor in the 400-500 time span.
Plot Nonlinearity Cross-Sections for Nonlinear ARX Models
Perform the following procedure to view the shape of the nonlinearity as a function of regressors on a Nonlinear ARX Model plot.
In the System Identification app, select the Nonlinear ARX check box to view the nonlinearity cross-sections.
By default, the plot shows the relationship between the output regressors
Height(t-1)andHeight(t-2). This plot shows a regular plane in the following figure. Thus, the relationship between the regressors and the output is approximately a linear plane.
In the Nonlinear ARX Model Plot window, set Regressor 1 to
Voltage(t-1). Set Regressor 2 toVoltage(t-2). Click Apply.The relationship between these regressors and the output is nonlinear, as shown in the following plot.

To rotate the nonlinearity surface, select Style > Rotate 3D and drag the plot to a new orientation.
To display a 1-D cross-section for Regressor 1, set Regressor 2 to
none, and click Apply. The following figure shows the resulting nonlinearity magnitude for Regressor 1, which represents the time-shifted voltage signal,Voltage(t-1).
Change Nonlinear ARX Model Structure
In this portion of the tutorial, you estimate a nonlinear ARX model with specific input delay and nonlinearity settings. Typically, you select model orders by trial and error until you get a model that produces an accurate fit to the data.
You must have already estimated the nonlinear ARX model with default settings, as described in Estimate Nonlinear ARX Model with Default Settings.
In the Estimate Nonlinear ARX Models dialog box, select the Model Structure tab, and then select the Regressors tab.
In the Configure: Linear regressors #1 panel, change the
Voltagevariable lags to[3 4]. This is because the data suggests that there is a minimum of 3 sample lags between the input and the output.This action updates the regressors list to show
Voltage(t-3)andVoltage(t-4)—terms with a minimum delay of three samples.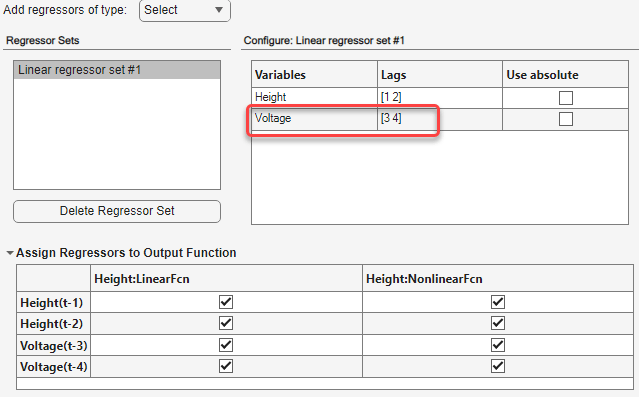
Click Estimate.
This action adds the model
nlarx2to the System Identification app and updates the Model Output window to include this model. Double-clicking on thenlarx2icon in the model board of the main app window shows the estimation results.
The app also updates the model output plot to display the fit of the model
nlarx2to the validation datasetzv. The plot shows that the choice of correct input variable lags improves the fit.
In the Estimate Nonlinear ARX Models dialog box, select the Model Structure tab, and then select the Output Function tab.
For the Number of Units, select Enter and enter
6. Setting a specific number controls the flexibility of the nonlinear function by directly specifying the number of wavelets that Wavelet Network uses.
Click Estimate.
This action adds the model
nlarx3to the System Identification app. It also updates the Model Output window, as shown in the following figure.
Use Polynomial Regressors
You can estimate a nonlinear ARX model that use higher powers of lagged variables as regressors. In this example, you will add second-order polynomials of the lagged variables, including cross terms.
In the Estimate Nonlinear ARX Models dialog, select the Model Structure tab and then select the Regressors tab.
Expand Add regressors of type and select Polynomial.

This action adds a polynomial regressor set called
Polynomial regressors #1to the list of regressor sets. By default, this set is configured to generate regressors of polynomial order two.Change the
Voltagelags to[3 4].Select Mix lags to include all cross terms. This action adds ten second-order regressors to the model, in addition to the four contributed by Linear regressor #1.

Click Estimate. This action adds the model
nlarx4to the app. The app updates the Model Output plot, as shown in the following figure.
The plot shows that the addition of polynomial regressors has not improved the generalization ability of the model. That is, the model does not provide a better fit between the model output and the measured output for independent validation data. This result is typically the scenario with overfits, that is, when the model contains more regressors than absolutely required.
Select Subset of Regressors in Nonlinear Block
You can estimate a nonlinear ARX model that includes only a subset of regressors that enter as inputs to the nonlinear block. By default, all regressors are used in the nonlinear block. In this portion of the tutorial, you assign only a subset of the regressors to the nonlinear block.
You must have already specified the model structure, as described in Change Nonlinear ARX Model Structure.
In the Estimate Nonlinear ARX Models dialog box, select the Model Structure tab, and then select the Regressors tab.
If collapsed, expand the Assign Regressors to Output Function panel.
Clear the selections for all the second order regressors from the Height:NonlinearFcn column of the table. Also, clear the selections for all the regressors with cross terms (that is, regressors composed of products of 2 terms) from Height:LinearFcn.

Click Estimate.
This action adds the model
nlarx5to the System Identification app. It also updates the Model Output window.

This model shows improved generalization ability.
Specify Previously Estimated Model with Different Output Function Nonlinearity
You can estimate a series of nonlinear ARX models by making systematic variations to
the model structure and base each new model on the configuration of a previously estimated
model. In this portion of the tutorial, you estimate a nonlinear ARX model that is similar
to an existing model (nlarx3), but which has a different nonlinearity
in the output function.
In the Estimate Nonlinear ARX Models dialog box, select the Model Structure tab.
Click Select next to Initialize using existing model (optional). In the Initialize Model dialog box, select
nlarx3from Nonlinear model and click OK. This sets the properties that are displayed in the Regressors and Output Function tabs to the values corresponding tonlarx3.
Select the Output Function tab.
In the table, change the choice of Nonlinear Function to
Sigmoid Network. This sets the output function to a sigmoid network.In Enter the number of units, enter
6.
Click Estimate.
This action adds the model
nlarx6to the System Identification app. It also updates the Model Output plot, as shown in the following figure.
Select the Best Model
The best model is the simplest model that accurately describes
the dynamics. The results indicate that model
nlarx3 is a candidate for
being the best idnlarx model for this data, based on the
various model structure choices that this example
explored.
Export Best Model to Base Workspace
Drag the nlarx3 icon to the
To Workspace box in the main System Identification app
window. Alternatively, double click the nlarx3 icon to open its
information board. From there, click Export to export the model to
the base workspace.

Estimate Hammerstein-Wiener Models
Estimate Hammerstein-Wiener Models with Default Settings
In this portion of the tutorial, you estimate nonlinear Hammerstein-Wiener models using default model structure and estimation options.
You must have already prepared the data, as described in Prepare Data. For more information about nonlinear ARX models, see What Is a Hammerstein-Wiener Model?
Note
The illustrations in this tutorial represent a typical System Identification app session. Your results may not precisely match the results in the images.
In the System Identification app, select Estimate > Hammerstein-Wiener Models to open the Estimate Hammerstein-Wiener Models dialog box. The dialog box contains two tabs — Model Structure and Estimation Options.
Inspect the default model structure. The Model Structure tab contains three tabs, one tab for each component of the model. These components are the input nonlinearity, the linear dynamic block, and the output nonlinearity.
Select the Input Nonlinearity tab. The default nonlinearity is a Piecewise Linear function with 10 breakpoints.

Select the Linear Block tab. The linear transfer function has a numerator order of 2, which implies a second-order polynomial in z-1, a denominator order of 3, and an input delay of 1 sample.

Select the Output Nonlinearity tab. As with the Input Nonlinearity tab, the default nonlinearity is a Piecewise Linear function with 10 breakpoints.

Click Estimate.
This action estimates the parameters of the Hammerstein-Wiener model to minimize the difference between the model output and the measured output (
ze.OutputData). The estimated parameters are:The breakpoint locations (x- and y-coordinates) of the input and output piecewise-linear functions.
The numerator and the denominator polynomial coefficients that compose the linear block transfer function.
The software adds the estimated model
nlhw1to the model board of the System Identification app.
In the System Identification app, select the Model output check box.
This action simulates the model using the input validation data as input to the model and plots the simulated output on top of the output validation data. Note that the validation data is set to
zv.
The Best Fits area of the Model Output window shows the agreement between the model output and the validation-data output.

The model
nlhw1does not validate well. The fit tozv.OutputDatais poor.
Plot Nonlinearities and Linear Transfer Function
You can plot the input/output nonlinearities and the linear transfer function of the model on a Hammerstein-Wiener plot.
In the System Identification app, select Hamm-Wiener to view the Hammerstein-Wiener model plot.
The plot displays the input nonlinearity, as shown in the following figure.

Click the yNL rectangle in the top portion of the Hammerstein-Wiener Model Plot window.
The plot updates to display the output nonlinearity.

Click the Linear Block rectangle in the top portion of the Hammerstein-Wiener Model Plot window.
The plot updates to display the step response of the linear transfer function.

In the Choose plot type list, select
Bode. This action displays a Bode plot of the linear transfer function.
Change Hammerstein-Wiener Model Input Delay
In this portion of the tutorial, you estimate a Hammerstein-Wiener model with a specific model order and nonlinearity settings. Typically, you select model orders and delays by trial and error until you get a model that produces a satisfactory fit to the data.
You must have already estimated the Hammerstein-Wiener model with default settings, as described in Estimate Hammerstein-Wiener Models with Default Settings.
In the Estimate Hammerstein-Wiener dialog box, select the Model Structure tab and then the Linear Block tab.
For the
Voltageinput channel, double-click the corresponding Input Delay (nk) cell and enter the value3.Click Estimate.
This action adds the model
nlhw2to the System Identification app and updates the Model Output plot, as shown in the following figure.
The Best Fits panel of the Model Output window shows the quality of the
nlhw2fit, which is an improvement over that of the modelnlhw1.
Change Nonlinearity Estimator in Hammerstein-Wiener Model
In this portion of the example, you modify the default Hammerstein-Wiener model structure by changing its nonlinearity estimator.
Tip
If you know that your system includes saturation or dead-zone nonlinearities, you
can specify these specialized nonlinearity estimators in your model.
Piecewise Linear, Wavelet
Network, and Sigmoid Network are nonlinearity
estimators for general nonlinearity approximation.
In the Estimate Hammerstein-Wiener Models dialog box, select the Model Structure tab and then the Input Nonlinearity tab.
Click the Nonlinearity cell for the
Voltagevariable and selectSigmoid Networkfrom the list.
In Enter the number of units, set the value to
20.
Click Estimate.
This action adds the model
nlhw3to the System Identification app. It also updates the Model Output window, as shown in the following figure.
In the Estimate Hammerstein-Wiener Models dialog box, select the Input Nonlinearity tab.
For the
Voltageinput, set Nonlinearity toWavelet Network. The default value for Number of Units is Select Automatically.
Select the Output Nonlinearity tab.
Set the
Heightoutput Nonlinearity toOne-dimensional Polynomial. Set Degree of polynomial to2.
Click Estimate.
This action adds the model
nlhw4to the System Identification app. It also updates the Model Output window, as shown in the following figure.
Select the Best Model
The best model is the simplest model that accurately describes the dynamics.
In this example, the models nlhw3 and nlhw4 are
good candidates.