Noise Cancellation in Simulink Using Normalized LMS Adaptive Filter

Create an Acoustic Environment in Simulink

Adaptive filters are filters whose coefficients or weights change over time to adapt to the statistics of a signal. They are used in a variety of fields including communications, controls, radar, sonar, seismology, and biomedical engineering.

In this topic, you learn how to create an acoustic environment that simulates both white noise and colored noise added to an input signal. You later use this environment to build a model capable of adaptive noise cancellation using adaptive filtering:

Open the Acoustic Noise Cancellation example model, dspanc in Acoustic Noise Cancellation (LMS).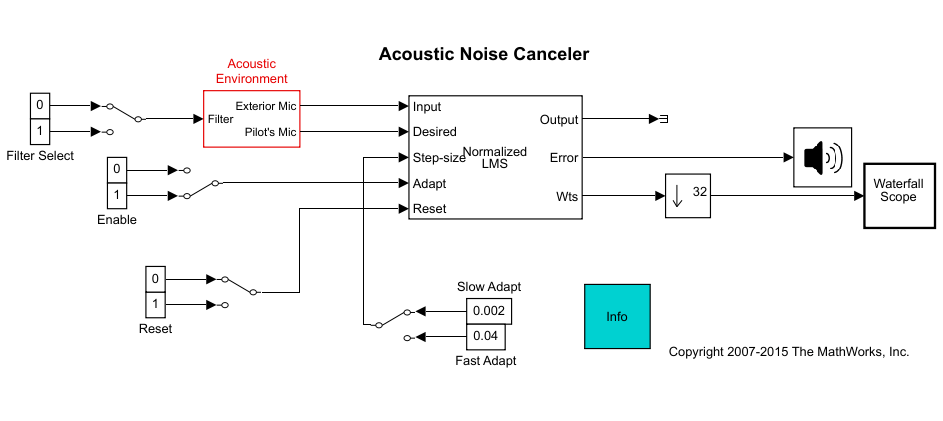
Copy and paste the subsystem called Acoustic Environment into a new model.
Double-click the Acoustic Environment subsystem.
Gaussian noise is used to create the signal sent to the Exterior Mic output port. If the input to the Filter port changes from 0 to 1, the Digital Filter block changes from a lowpass filter to a bandpass filter. The filtered noise output from the Digital Filter block is added to signal coming from a .wav file to produce the signal sent to the Pilot's Mic output port.

You have now created an acoustic environment. In the following topics, you use this acoustic environment to produce a model capable of adaptive noise cancellation.

LMS Filter Configuration for Adaptive Noise Cancellation

This example uses:

Open Model

In the previous topic, Create an Acoustic Environment in Simulink, you created a system that produced two output signals. The signal output at the Exterior Mic port is composed of white noise. The signal output at the Pilot's Mic port is composed of colored noise added to a signal from a .wav file. In this topic, you create an adaptive filter to remove the noise from the Pilot's Mic signal. This topic assumes that you are working on a Windows operating system.

If the model you created in Create an Acoustic Environment in Simulink is not open on your desktop, you can open the equivalent model ex_adapt1_audio.

From the DSP System Toolbox Filtering library, and then from the Adaptive Filters library, click-and-drag an LMS Filter block into the model that contains the Acoustic Environment subsystem.

Double-click the LMS Filter block. Set the block parameters as follows, and then click OK:

Algorithm = Normalized LMS
Filter length = 40
Step size (mu) = 0.002
Leakage factor (0 to 1) = 1

The block uses the normalized LMS algorithm to calculate the forty filter coefficients. Setting the Leakage factor (0 to 1) parameter to 1 means that the current filter coefficient values depend on the filter's initial conditions and all of the previous input values.

Click-and-drag the following blocks into your model.

Two Constant blocks from the Simulink/Sources library
Manual Switch block from the Simulink/Signal Routing library
Terminator block from the Simulink/Sinks library
Downsample block from the Signal Operations library
Audio Device Writer block from the Sinks library
Waterfall Scope block from the Sinks library

Connect the blocks so that your model resembles the following figure.

Double-click the Constant block. Set the Constant value parameter to 0 and then click OK.

Double-click the Downsample block. Set the Downsample factor, K parameter to 32. Click OK.

The filter weights are being updated so often that there is very little change from one update to the next. To see a more noticeable change, you need to downsample the output from the Wts port.

Double-click the Waterfall Scope block. The Waterfall scope window opens. Click the Scope parameters button.

The Parameters window opens.

Click the Axes tab. Set the parameters as follows:

Y Min = -0.188
Y Max = 0.179

Click the Data history tab. Set the parameters as follows:

History traces = 50
Data logging = All visible

Close the Parameters window leaving all other parameters at their default values. You might need to adjust the axes in the Waterfall scope window in order to view the plots.

Click the Fit to view button in the Waterfall scope window. Then, click-and-drag the axes until they resemble the following figure.

In the Modeling tab, click Model Settings. In the Solver pane, set the parameters as follows, and then click OK:

Stop time = inf
Type = Fixed-step
Solver = Discrete (no continuous states)

Run the simulation and view the results in the Waterfall scope window. You can also listen to the simulation using the speakers attached to your computer.

Experiment with changing the Manual Switch so that the input to the Acoustic Environment subsystem is either 0 or 1. When the value is 0, the Gaussian noise in the signal is being filtered by a lowpass filter. When the value is 1, the noise is being filtered by a bandpass filter. The adaptive filter can remove the noise in both cases.

You have now created a model capable of adaptive noise cancellation. The adaptive filter in your model is able to filter out both low frequency noise and noise within a frequency range. In the next topic, Modify Adaptive Filter Parameters During Model Simulation, you modify the LMS Filter block and change its parameters during simulation.

Modify Adaptive Filter Parameters During Model Simulation

This example uses:

Open Model

In the previous topic, LMS Filter Configuration for Adaptive Noise Cancellation, you created an adaptive filter and used it to remove the noise generated by the Acoustic Environment subsystem. In this topic, you modify the adaptive filter and adjust its parameters during simulation. This topic assumes that you are working on a Windows operating system.

If the model you created in Create an Acoustic Environment in Simulink is not open on your desktop, open the equivalent model ex_adapt2_audio.

Double-click the LMS filter block. Set the block parameters as follows, and then click OK:

Specify step size via = Input port
Initial value of filter weights = 0
Select the Adapt port check box
Reset port = Non-zero sample

The LMS Filter dialog box should now look similar to the following figure.

Step-size, Adapt, and Reset ports appear on the LMS Filter block.

Click-and-drag the following blocks into your model.

Six Constant blocks from the Simulink/Sources library
Three Manual Switch blocks from the Simulink/Signal Routing library

Connect the blocks as shown in the following figure.

Double-click the Constant2 block. Set the block parameters as follows, and then click OK:

Constant value = 0.002
Select the Interpret vector parameters as 1-D check box
Sample time (-1 for inherited) = inf
Output data type mode = Inherit via back propagation

Double-click the Constant3 block. Set the block parameters as follows, and then click OK:

Constant value = 0.04
Select the Interpret vector parameters as 1-D check box
Sample time (-1 for inherited) = inf
Output data type mode = Inherit via back propagation

Double-click the Constant4 block. Set the Constant value parameter to 0 and then click OK.

Double-click the Constant6 block. Set the Constant value parameter to 0 and then click OK.

In the Debug tab, select Information Overlays > Nonscalar Signals and Signal Dimensions.

Double-click Manual Switch2 so that the input to the Adapt port is 1.

Run the simulation and view the results in the Waterfall scope window. You can also listen to the simulation using the speakers attached to your computer.

Double-click the Manual Switch block so that the input to the Acoustic Environment subsystem is 1. Then, double-click Manual Switch2 so that the input to the Adapt port to 0.

The filter weights displayed in the Waterfall scope window remain constant. When the input to the Adapt port is 0, the filter weights are not updated.

Double-click Manual Switch2 so that the input to the Adapt port is 1. The LMS Filter block updates the coefficients.

Connect the Manual Switch1 block to the Constant block that represents 0.002. Then, change the input to the Acoustic Environment subsystem. Repeat this procedure with the Constant block that represents 0.04.

You can see that the system reaches steady state faster when the step size is larger.

Double-click the Manual Switch3 block so that the input to the Reset port is 1.

The block resets the filter weights to their initial values. In the LMS Filter dialog box, from the Reset port list, you chose Non-zero sample. This means that any nonzero input to the Reset port triggers a reset operation.

You have now experimented with adaptive noise cancellation using the LMS Filter block. You adjusted the parameters of your adaptive filter and viewed the effects of your changes while the model was running.

For more information about adaptive filters, see the following block reference pages:

References

[1] Hayes, Monson H., Statistical Digital Signal Processing and Modeling. Hoboken, NJ: John Wiley & Sons, 1996, pp.493–552.

[2] Haykin, Simon, Adaptive Filter Theory. Upper Saddle River, NJ: Prentice-Hall, Inc., 1996.