LMS Filter
Compute output, error, and weights using least mean squares (LMS) adaptive algorithm
Libraries:
DSP System Toolbox /
Filtering /
Adaptive Filters
DSP System Toolbox HDL Support /
Filtering
Description
The LMS Filter block can implement an adaptive FIR filter by using five different algorithms. The block estimates the filter weights or coefficients needed to minimize the error, e(n), between the output signal y(n) and the desired signal, d(n). The output is the filtered input signal, which is the estimate of the desired signal. The Error port outputs the result of subtracting the output signal from the desired signal.
Under specific conditions, this block also supports SIMD code generation. For details, see Code Generation.
Examples
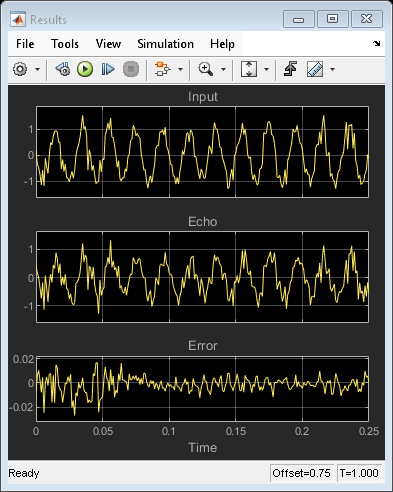
Time-Delay Channel Estimation Through Adaptive Filtering
Adaptively estimate the time delay for a noisy input signal using the LMS adaptive FIR algorithm.
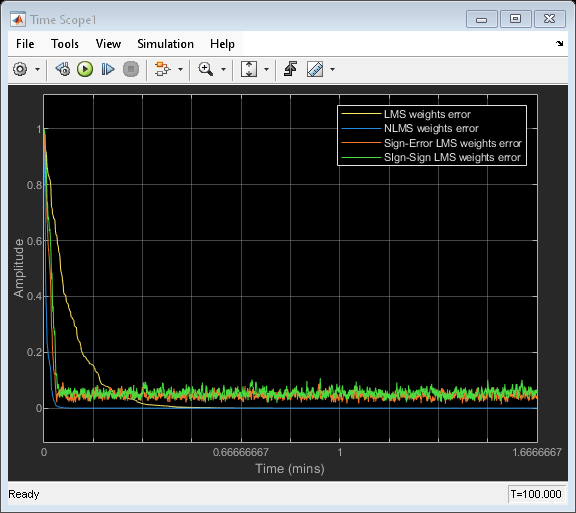
Adaptive Filter Convergence
Compares the rate of convergence for adaptive filters using different LMS algorithms.
Ports
Input
Input signal, specified as a scalar or column vector.
When the input is fixed-point, it must be signed.
When you set the Algorithm parameter to
Sign—Error LMS,
Sign—Data LMS, or
Sign—Sign LMS, the data input
through the Input port must be real.
Data Types: single | double | fixed point
Desired signal, specified as a scalar or column vector. The desired
signal must have the same data type, complexity, and dimensions as the
Input signal.
When Input is fixed-point, the desired signal must be a signed fixed-point.
When you set the Algorithm parameter to
Sign—Error LMS,
Sign—Data LMS, or
Sign—Sign LMS, the data input
through the Desired port must be real.
Data Types: single | double | fixed point
Enter the step size μ. For convergence of the
normalized LMS equations, 0<µ<2. Input type
must match the type of the Input port.
When Input is fixed-point, the step-size must be a signed fixed-point.
Dependencies
This port appears only when you set the Specify step size via parameter to
Input port.
Data Types: single | double | fixed point
When the input to this port is greater than zero, the block continuously updates the filter weights. When the input to this port is less than or equal to zero, the filter weights remain at their current values.
Dependencies
This port appears only when you set the Adapt port parameter to
on.
Data Types: single | double | int8 | int16 | int32 | Boolean
Signal to reset the value of the filter weights to their initial values, specified as a scalar. The block resets the filter weights whenever a reset event is detected at the Reset port. The reset signal rate must be the same rate as the data signal input.
For reset event types, see the Reset parameter.
Dependencies
This port appears only when you set the Reset
port parameter to Rising
edge, Falling edge,
Either edge, or Non-zero
sample.
Data Types: single | double | int8 | int16 | int32 | Boolean
Output
Estimate of the desired signal, returned as a scalar or a column vector. It is the same size and complexity as the input signal.
The output signal has the same data type as the desired signal.
Data Types: single | double | fixed point
Error between the output and desired signals, returned as a scalar or a column vector. This error is the result of subtracting the output signal from the desired signal.
The error signal has the same data type as the desired signal.
Data Types: single | double | fixed point
Filter weights, returned as a scalar or a column vector. For each iteration, the block outputs the current updated filter weights from this port.
The weights data type must match the type of the Input port for floating-point signals. Obeys the
Weights parameter for fixed-point signals.
Dependencies
This port appears only when you set the Output filter weights parameter to
On.
Data Types: single | double | fixed point
Parameters
Main Tab
Choose the algorithm used to calculate the filter weights.
Enter the length of the FIR filter weights vector.
Dialog–– Specify step size by using the Step size (mu) parameter.Input port–– Specify step size by using theStep-sizeport.
Enter the step size μ. For convergence of the normalized LMS equations, 0<µ<2.
Tunable: Yes
Dependencies
This parameter appears only when you set the Specify step size via parameter to
Dialog.
Enter the leakage factor, 0 < 1 – μα ≤ 1.
Tunable: Yes
Enter the initial filter weights w(0) as a vector or a scalar. When you enter a scalar, the block uses the scalar value to create a vector of filter weights. This vector length is equal to the filter length and all of its values are equal to the scalar value.
Select this check box to enable the Adapt input port.
When you want to reset the value of filter weights to their initial values, use the Reset port parameter. The reset signal must be the same rate as the data signal input.
Select None to disable the Reset port. To enable the Reset
port, select one of the following from the list:
Rising edge— Triggers a reset operation when the Reset input does one of the following:Rises from a negative value to a positive value or zero
Rises from zero to a positive value, where the rise is not a continuation of a rise from a negative value to zero (see the following figure)

Falling edge— Triggers a reset operation when the Reset input does one of the following:Falls from a positive value to a negative value or zero
Falls from zero to a negative value, where the fall is not a continuation of a fall from a positive value to zero (see the following figure)

Either edge— Triggers a reset operation when the Reset input is aRising edgeorFalling edgeNon-zero sample— Triggers a reset operation at each sample time that the Reset input is not zero
Select the Output filter weights parameter to
export the filter weights from the Wts port. For each iteration, the block outputs the
current updated filter weights from this port.
Data Type Tab
Specify the rounding mode for fixed-point operations as one of the following:
FloorCeilingConvergentNearestRoundSimplestZero
For more details, see rounding mode.
When you select this parameter, the block saturates the result of its
fixed-point operation. When you clear this parameter, the block wraps
the result of its fixed-point operation. For details on
saturate and wrap, see overflow
mode for fixed-point operations.
Choose how you specify the word length and the fraction length of the leakage factor and step size:
Same word length as first input–– The word length of the leakage factor and step size match that of the first input to the block. In this mode, the fraction length of the leakage factor and step size is automatically set to the binary-point only scaling that provides you with the best precision possible given the value and word length of the coefficients.Specify word length–– You can enter the word length of the leakage factor and step size, in bits. In this mode, the fraction length of the leakage factor and step size is automatically set to the binary-point only scaling that provides you with the best precision possible given the value and word length of the coefficients.Binary point scaling–– You can enter the word length and the fraction length of the leakage factor and step size, in bits. The leakage factor and the step size must have the same word length, but the fraction lengths can differ.
For the Specify
step size via parameter, if you choose Input
port, the word length of the leakage factor is the
same as the word length of the step size input at the Step-size port. The fraction length of the leakage
factor is automatically set to the best precision possible based on the
word length of the leakage factor.
Dependencies
This parameter is visible only if you set the Specify
step size via parameter to
Dialog
Choose how you specify the word length and fraction length of the filter weights of the block:
Same as first input–– The word length and fraction length of the filter weights match those of the first input to the block.Binary point scaling–– You can enter the word length and the fraction length of the filter weights, in bits.
Choose how you specify the word length and fraction length of u'u, W'u, , , and the quotient, Q. Here, u is the input vector, W is the vector of filter weights, μ is the step size, e is the error, and Q is the quotient, which is defined as
Same as first input–– The word length and fraction length of these quantities match those of the first input to the block.Binary point scaling–– You can enter the word length and the fraction length of these quantities, in bits. The word length of the quantities must be the same, but the fraction lengths can differ.
Use this parameter to specify how you want to designate the word and fraction lengths of the accumulators for the u'u and W'u operations.
Note
Do not use this parameter to designate the word and fraction lengths of the accumulator for the operation. The accumulator data type for this quantity is automatically set to be the same as the product data type. The minimum, maximum, and overflow information for this accumulator is logged as part of the product information. Autoscaling treats this product and accumulator as one data type.
Same as first input–– These characteristics match those of the input to the block.Binary point scaling–– You can enter the word length and the fraction length of the accumulators, in bits. The word length of both the accumulators must be the same, but the fraction lengths can differ.
For illustrations depicting the use of the accumulator data type in this block, see Fixed-Point Data Types and Multiplication Data Types.
Select this parameter to prevent the fixed-point tools from overriding the data types you specify in the block dialog box.
Block Characteristics
Data Types |
|
Direct Feedthrough |
|
Multidimensional Signals |
|
Variable-Size Signals |
|
Zero-Crossing Detection |
|
More About
When you select LMS for the Algorithm parameter, the block calculates the filter weights by
using the least mean-square (LMS) algorithm. This algorithm is defined by these equations.
The various LMS adaptive filter algorithms available in this block are defined as:
LMS ––
Normalized LMS ––
In Normalized LMS, to overcome potential numerical instability in the update of the weights, a small positive constant, ε, has been added in the denominator. For double-precision floating-point input, ε is the output of the
epsfunction. For single-precision floating-point input, ε is the output ofeps("single"). For fixed-point input, ε is 0.Sign-Error LMS ––
Sign-Data LMS ––
where u(n) is real.
Sign-Sign LMS ––
where u(n) is real.
| Variable | Description |
|---|---|
n | The current time index |
u(n) | The vector of buffered input samples at step n |
u*(n) | The complex conjugate of the vector of buffered input samples at step n |
w(n) | The vector of filter weight estimates at step n |
y(n) | The filtered output at step n |
e(n) | The estimation error at step n |
d(n) | The desired response at step n |
µ | The adaptation step size |
| α | The leakage factor (0 < α ≤ 1) |
ε | A constant that corrects any potential numerical instability that occurs during the update of weights. |
The following diagrams show the data types used within the LMS Filter block for fixed-point signals. The table summarizes the definitions of variables used in the diagrams.
| Variable | Definition |
|---|---|
u | Input vector |
W | Vector of filter weights |
µ | Step size |
e | Error |
Q | Quotient, |
Product u'u | Product data type in Energy calculation diagram |
Accumulator u'u | Accumulator data type in Energy calculation diagram |
Product W'u | Product data type in Convolution diagram |
Accumulator W'u | Accumulator data type in Convolution diagram |
Product | Product data type in Product of step size and error diagram |
Product | Product and accumulator data type in Weight update diagram. 1 |
1The accumulator data type for this quantity is automatically set to be the same as the product data type. The minimum, maximum, and overflow information for this accumulator is logged as part of the product information. Autoscaling treats this product and accumulator as one data type.


You can set the data type of the parameters, weights, products, quotient, and accumulators in the block mask. Fixed-point inputs, outputs, and mask parameters of this block must have these characteristics:
The input signal and the desired signal must have the same word length, but their fraction lengths can differ.
The step size and leakage factor must have the same word length, but their fraction lengths can differ.
The output signal and the error signal have the same word length and the same fraction length as the desired signal.
The quotient and the product output of the u'u, W'u, , and operations must have the same word length, but their fraction lengths can differ.
The accumulator data type of the u'u and W'u operations must have the same word length, but their fraction lengths can differ.
The output of the multiplier is in the product output data type if at least one of the inputs to the multiplier is real. If both of the inputs to the multiplier are complex, the result of the multiplication is in the accumulator data type. For details, see Multiplication Data Types.
References
[1] Hayes, M.H. Statistical Digital Signal Processing and Modeling. New York: John Wiley & Sons, 1996.
Extended Capabilities
Generated code relies on the memcpy or
memset function (string.h) under certain
conditions.
Generate SIMD code using Intel® AVX2 code replacement library
Note
Requires Embedded Coder® license
The LMS Filter block supports SIMD code generation using Intel AVX2 code replacement library under these conditions:
You set Algorithm to
LMSorNormalized LMS.Input signal is real-valued.
Input signal has a data type of
singleordouble.
To generate SIMD code from this block using this workflow, see Use Intel AVX2 Code Replacement Library to Generate SIMD Code from Simulink Blocks.
Generate SIMD code by leveraging target hardware instruction set extensions (since R2023b)
Note
Requires Simulink® Coder™ or Embedded Coder license
You can generate SIMD code for the LMS Filter block on all Intel platforms, ARM® Cortex®-A processors, and Apple silicon processors by using the model configuration parameter Leverage target hardware instruction set extensions under these conditions:
You set Algorithm to
Sign-Error LMS,Sign-Data LMS,Sign-Sign LMS,LMSorNormalized LMS.Input signal is real-valued with real filter coefficients
Input signal is complex-valued with real or complex filter coefficients.
Data type of the input signal is
single(ARM Cortex-A processors)Data type of the input signal is
singleordouble(Intel platforms)
In addition, configure your model appropriately. In the Modeling tab of the Simulink model window, click Model Settings and configure these parameters under Code Generation.
In the Optimization pane:
Provide a specific instruction set in the Leverage target hardware instruction set extensions parameter.
Select the Optimize reductions parameter.
Under Optimization levels, set Level to
Maximumand Priority toMaximize execution speed.
In the Interface pane, under Software environment, clear non-finite numbers.
To generate SIMD code from this block using this workflow, see Use Target Hardware Instruction Set Extensions to Generate SIMD Code from Simulink Blocks for Intel Platforms, Use Target Hardware Instruction Set Extensions to Generate SIMD Code from Simulink Blocks for Apple silicon, and Use Target Hardware Instruction Set Extensions to Generate SIMD Code from Simulink Blocks for ARM Cortex-A Processors.
For computationally intensive operations on supported blocks, SIMD intrinsics can significantly improve the performance of the generated code on Intel platforms. For more details, see Optimize Code for Reduction Operations by Using SIMD (Simulink Coder).
For more information on SIMD code generation in DSP System Toolbox™, see SIMD Code Generation.
HDL Coder™ provides additional configuration options that affect HDL implementation and synthesized logic.
Note
For a LMS filter with hardware-friendly control signals and simulation of HDL latency in Simulink, or for complex data with complex coefficients, use the LMS Filter (DSP HDL Toolbox) block instead of this block.
By default, the LMS Filter implementation uses a linear sum for the FIR section of the filter.
The LMS Filter implements a tree summation (which has a shorter critical path) under the following conditions:
The LMS Filter is used with real data.
The word length of the Accumulator W'u data type is at least
ceil(log2(filter length))bits wider than the word length of the Product W'u data type.The Accumulator W'u data type has the same fraction length as the Product W'u data type.
| ConstrainedOutputPipeline | Number of registers to place at
the outputs by moving existing delays within your design. Distributed
pipelining does not redistribute these registers. The default is
|
| InputPipeline | Number of input pipeline stages
to insert in the generated code. Distributed pipelining and constrained
output pipelining can move these registers. The default is
|
| OutputPipeline | Number of output pipeline stages
to insert in the generated code. Distributed pipelining and constrained
output pipelining can move these registers. The default is
|
This block supports code generation for complex signals.
HDL Coder does not support the
Normalized LMSalgorithm of the LMS Filter.The
Resetport supports onlyBooleanandunsignedinputs.The
Adaptport supports onlyBooleaninputs.Filter length must be greater than or equal to 2.
Version History
Introduced before R2006aIn R2024b, if you have Embedded Coder, you can generate SIMD code for the LMS Filter block for Apple silicon processors by using the model configuration parameter Leverage target hardware instruction set extensions. For more information, see Use Target Hardware Instruction Set Extensions to Generate SIMD Code from Simulink Blocks for Apple silicon.
In R2023b, if you have Embedded Coder, you can generate SIMD code for the LMS Filter block when the input signal is complex-valued by using the model configuration parameter Leverage target hardware instruction set extensions.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)