Time-Delay Channel Estimation Through Adaptive Filtering
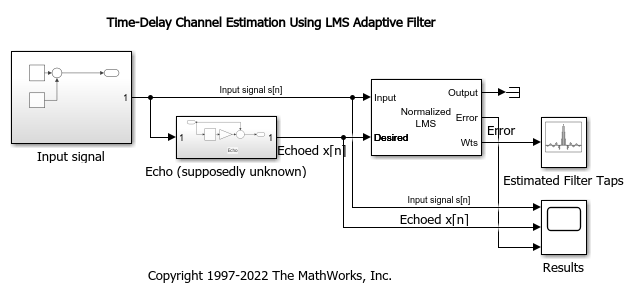
This example shows how to adaptively estimate the time delay for a noisy input signal using the LMS adaptive FIR algorithm.
Assume a signal ![$s[n] = a[n]+w[n]$](../../examples/dsp/win64/TimeDelayEstimationExample_eq06832886970054782519.png) where
where ![$w[n]$](../../examples/dsp/win64/TimeDelayEstimationExample_eq03178806122892290353.png) is a white Gaussian process and
is a white Gaussian process and ![$a[n]$](../../examples/dsp/win64/TimeDelayEstimationExample_eq00107744878115963933.png) is deterministic. The signal is measured with an echo of
is deterministic. The signal is measured with an echo of 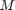 samples and attenuation
samples and attenuation  (both are unknown), resulting in the overall measurement:
(both are unknown), resulting in the overall measurement:
![$$ x[n] = s[n] + \alpha s[n-M] $$](../../examples/dsp/win64/TimeDelayEstimationExample_eq12097827341678758989.png)
The goal is to estimate the delay 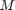 and the echo attenuation
and the echo attenuation  . One can determine these parameters by solving the filter identification problem
. One can determine these parameters by solving the filter identification problem 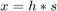 for
for 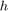 , combined with the prior
, combined with the prior ![$h[n] = \delta[n]+\alpha s[n-M]$](../../examples/dsp/win64/TimeDelayEstimationExample_eq11860339517273811776.png) . Provided that the filter
. Provided that the filter 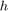 can be identified from the measurements signal
can be identified from the measurements signal  and the original signal
and the original signal  , one can derive
, one can derive  and
and 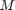
Such a filter identification problem can be posed in terms of adaptive LTI filtering. The reference signal is ![$d[n] = x[n]$](../../examples/dsp/win64/TimeDelayEstimationExample_eq08782681346033574520.png) , the input feed is
, the input feed is ![$s[n]$](../../examples/dsp/win64/TimeDelayEstimationExample_eq03923724676957201790.png) , and the adaptive filter is
, and the adaptive filter is 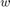 . Clearly, if the adaptation process concludes with
. Clearly, if the adaptation process concludes with 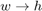 then the error signal
then the error signal 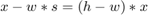 vanishes.
vanishes.
There are numerous adaptive filtering algorithms. For this particular problem setup and signal model, the normalized LMS algorithm is suitable, and is available in the LMS Filter block.
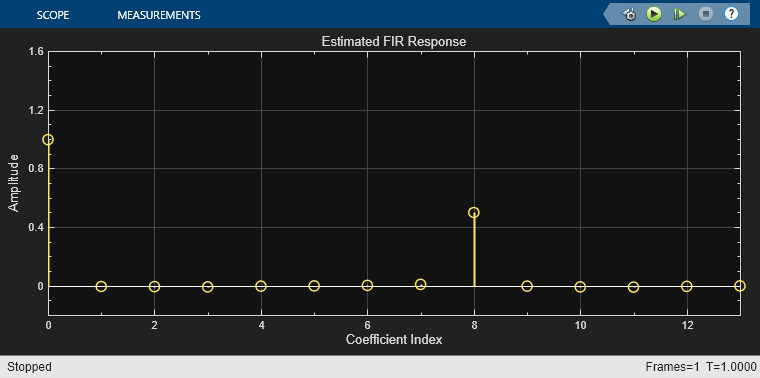
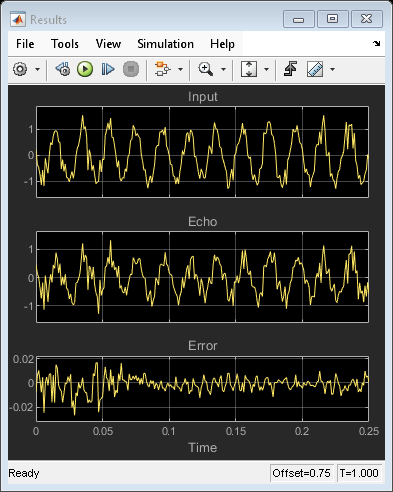
Run the simulation. The peaks in the filter taps vector indicates the time-delay estimate. In this case 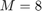 and
and 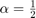 .
.
For details, see S. Haykin, Adaptive Filter Theory, 3rd Ed., Prentice-Hall 1996.