ldpcDecode
Syntax
Description
[
decodes the input log-likelihood ratio (LLR), Y,actualnumiter,finalparitychecks] = ldpcDecode(llr,decodercfg,maxnumiter)llr, using the
LDPC matrix specified by the input ldpcDecoderConfig
configuration object, decodercfg. A
positive LLR indicates that the corresponding bit is more likely a zero. Decoding terminates
when all of the parity checks are satisfied, up to a maximum number of iterations specified
by the input maxnumiter. LDPC
codes are linear error control codes with sparse parity-check matrices and long block
lengths that can attain performance near the Shannon limit.
[
specifies additional name-value arguments. For example,
Y,actualnumiter,finalparitychecks] = ldpcDecode(llr,decodercfg,maxnumiter,Name=Value)DecisionType='soft' specifies soft-decision decoding and outputs
LLRs.
Examples
Initialize parameters for the prototype matrix and block size to configure a rate 3/4 LDPC code specified in IEEE® 802.11. Create the parity-check matrix by using the ldpcQuasiCyclicMatrix function.
P = [
16 17 22 24 9 3 14 -1 4 2 7 -1 26 -1 2 -1 21 -1 1 0 -1 -1 -1 -1
25 12 12 3 3 26 6 21 -1 15 22 -1 15 -1 4 -1 -1 16 -1 0 0 -1 -1 -1
25 18 26 16 22 23 9 -1 0 -1 4 -1 4 -1 8 23 11 -1 -1 -1 0 0 -1 -1
9 7 0 1 17 -1 -1 7 3 -1 3 23 -1 16 -1 -1 21 -1 0 -1 -1 0 0 -1
24 5 26 7 1 -1 -1 15 24 15 -1 8 -1 13 -1 13 -1 11 -1 -1 -1 -1 0 0
2 2 19 14 24 1 15 19 -1 21 -1 2 -1 24 -1 3 -1 2 1 -1 -1 -1 -1 0
];
blockSize = 27;
pcmatrix = ldpcQuasiCyclicMatrix(blockSize,P);Create LDPC encoder and decoder configuration objects, displaying their properties.
cfgLDPCEnc = ldpcEncoderConfig(pcmatrix)
cfgLDPCEnc =
ldpcEncoderConfig with properties:
ParityCheckMatrix: [162×648 logical]
Read-only properties:
BlockLength: 648
NumInformationBits: 486
NumParityCheckBits: 162
CodeRate: 0.7500
cfgLDPCDec = ldpcDecoderConfig(pcmatrix)
cfgLDPCDec =
ldpcDecoderConfig with properties:
ParityCheckMatrix: [162×648 logical]
Algorithm: 'bp'
Read-only properties:
BlockLength: 648
NumInformationBits: 486
NumParityCheckBits: 162
CodeRate: 0.7500
Transmit an LDPC-encoded, M-QAM-modulated bit stream through an AWGN channel. Demodulate the signal, decode the received codewords, and then count bit errors. Use a for loop to process multiple SNR settings with and without LDPC forward error correction (FEC) coding of the transmitted data.
M = 64; maxnumiter = 10; snr = [0.5 1 1.5 2]; numframes = 20000; for ii = 1:length(snr) data = randi([0 1],cfgLDPCEnc.NumInformationBits,numframes,'int8'); % Transmit and receive with LDPC coding encodedData = ldpcEncode(data,cfgLDPCEnc); modSignal = qammod(encodedData,M,InputType='bit'); [rxsig, noisevar] = awgn(modSignal,snr(ii)); llrOut = qamdemod(rxsig,M, ... OutputType='approxllr', ... % Or use 'llr' for exact but slower LLR calculation NoiseVariance=noisevar); rxbits = ldpcDecode(llrOut,cfgLDPCDec,maxnumiter); fprintf(['SNR = %2.1f\n Coded: Error rate = %1.6f, ' ... 'Number of errors = %d\n'], ... snr(ii),nnz(data~=rxbits)/numel(data),nnz(data~=rxbits)); % Transmit and receive with no LDPC coding noCoding = qammod(data,M,InputType='bit'); rxNoCoding = awgn(noCoding,snr(ii)); rxBitsNoCoding = qamdemod(rxNoCoding,M,OutputType='bit'); fprintf(['Noncoded: Error rate = %1.6f, ' ... 'Number of errors = %d\n\n'], ... nnz(data~=rxBitsNoCoding)/numel(data),nnz(data~=rxBitsNoCoding)) end
SNR = 0.5 Coded: Error rate = 0.000441, Number of errors = 4282
Noncoded: Error rate = 0.039045, Number of errors = 379515
SNR = 1.0 Coded: Error rate = 0.000062, Number of errors = 604
Noncoded: Error rate = 0.032813, Number of errors = 318941
SNR = 1.5 Coded: Error rate = 0.000003, Number of errors = 27
Noncoded: Error rate = 0.027001, Number of errors = 262450
SNR = 2.0 Coded: Error rate = 0.000000, Number of errors = 0
Noncoded: Error rate = 0.021778, Number of errors = 211686
Initialize parameters for the prototype matrix and block size to configure a rate 3/4 LDPC code specified in IEEE® 802.11. Create the parity-check matrix by using the ldpcQuasiCyclicMatrix function.
P = [
16 17 22 24 9 3 14 -1 4 2 7 -1 26 -1 2 -1 21 -1 1 0 -1 -1 -1 -1
25 12 12 3 3 26 6 21 -1 15 22 -1 15 -1 4 -1 -1 16 -1 0 0 -1 -1 -1
25 18 26 16 22 23 9 -1 0 -1 4 -1 4 -1 8 23 11 -1 -1 -1 0 0 -1 -1
9 7 0 1 17 -1 -1 7 3 -1 3 23 -1 16 -1 -1 21 -1 0 -1 -1 0 0 -1
24 5 26 7 1 -1 -1 15 24 15 -1 8 -1 13 -1 13 -1 11 -1 -1 -1 -1 0 0
2 2 19 14 24 1 15 19 -1 21 -1 2 -1 24 -1 3 -1 2 1 -1 -1 -1 -1 0
];
blockSize = 27;
pcmatrix = ldpcQuasiCyclicMatrix(blockSize,P);Create LDPC encoder and decoder configuration objects, displaying their properties.
cfgLDPCEnc = ldpcEncoderConfig(pcmatrix)
cfgLDPCEnc =
ldpcEncoderConfig with properties:
ParityCheckMatrix: [162×648 logical]
Read-only properties:
BlockLength: 648
NumInformationBits: 486
NumParityCheckBits: 162
CodeRate: 0.7500
cfgLDPCDec = ldpcDecoderConfig(pcmatrix)
cfgLDPCDec =
ldpcDecoderConfig with properties:
ParityCheckMatrix: [162×648 logical]
Algorithm: 'bp'
Read-only properties:
BlockLength: 648
NumInformationBits: 486
NumParityCheckBits: 162
CodeRate: 0.7500
Transmit an LDPC-encoded, QPSK-modulated bit stream through an AWGN channel. Demodulate the signal, decode the received codewords, and then count bit errors. Use nested for loops to process multiple SNR settings and frames with and without LDPC forward error correction (FEC) coding of the transmitted data.
M = 4; maxnumiter = 10; snr = [3 6 20]; numframes = 10; ber = comm.ErrorRate; ber2 = comm.ErrorRate; for ii = 1:length(snr) for counter = 1:numframes data = randi([0 1],cfgLDPCEnc.NumInformationBits,1,'int8'); % Transmit and receive with LDPC coding encodedData = ldpcEncode(data,cfgLDPCEnc); modSignal = pskmod(encodedData,M,InputType='bit'); [rxsig, noisevar] = awgn(modSignal,snr(ii)); demodSignal = pskdemod(rxsig,M, ... OutputType='approxllr', ... NoiseVariance=noisevar); rxbits = ldpcDecode(demodSignal,cfgLDPCDec,maxnumiter); errStats = ber(data,rxbits); % Transmit and receive with no LDPC coding noCoding = pskmod(data,M,InputType='bit'); rxNoCoding = awgn(noCoding,snr(ii)); rxBitsNoCoding = pskdemod(rxNoCoding,M,OutputType='bit'); errStatsNoCoding = ber2(data,int8(rxBitsNoCoding)); end fprintf(['SNR = %2d\n Coded: Error rate = %1.2f, ' ... 'Number of errors = %d\n'], ... snr(ii),errStats(1),errStats(2)) fprintf(['Noncoded: Error rate = %1.2f, ' ... 'Number of errors = %d\n'], ... errStatsNoCoding(1),errStatsNoCoding(2)) reset(ber); reset(ber2); end
SNR = 3 Coded: Error rate = 0.07, Number of errors = 355
Noncoded: Error rate = 0.08, Number of errors = 384
SNR = 6 Coded: Error rate = 0.00, Number of errors = 0
Noncoded: Error rate = 0.02, Number of errors = 98
SNR = 20 Coded: Error rate = 0.00, Number of errors = 0
Noncoded: Error rate = 0.00, Number of errors = 0
Use a GPU to accelerate LDPC encoding, PSK modulation, AWGN channel modeling, PSK demodulation, LDPC decoding, and bit error rate computation. In this example you compute the error statistics for the belief propagation decoding algorithm and the normalized min-sum decoding algorithm.
Create LDPC Configuration Objects
Create an LDPC encoder configuration object and an LDPC decoder configuration object. Define simulation variables.
% Use ldpcQuasiCyclicMatrix to create a parity-check matrix load("LDPCExamplePrototypeMatrix.mat","P"); % A prototype matrix from the 5G standard blockSize = 384; H = ldpcQuasiCyclicMatrix(blockSize, P); encoderCfg = ldpcEncoderConfig(H); decoderCfg1 = ldpcDecoderConfig(encoderCfg); % The default algorithm is "bp" decoderCfg2 = ldpcDecoderConfig(encoderCfg,"norm-min-sum"); M = 4; % Modulation order (QPSK) snr = [-2 -1.5 -1]; numFramesPerCall = 50; numCalls = 40; maxNumIter = 20; s = rng(1235); % Fix random seed errRate = zeros(length(snr),2);
Compute Bit Error Rates
Generate random bits in a gpuArray (Parallel Computing Toolbox) object and let its data flow through the ldpcEncode, pskmod, awgn, pskdemod, ldpcDecode, and biterr functions. For each SNR setting, compute the error statistics for the belief propagation decoding algorithm and the normalized min-sum decoding algorithm.
for ii = 1:length(snr) ttlErr = [0 0]; noiseVariance = 1/10^(snr(ii)/10); for counter = 1:numCalls data = gpuArray.randi([0 1],encoderCfg.NumInformationBits,numFramesPerCall,'logical'); % Transmit and receive LDPC coded signal data encData = ldpcEncode(data,encoderCfg); modSig = pskmod(encData,M,pi/4,'InputType','bit'); rxSig = awgn(modSig,snr(ii)); % Signal power = 0 dBW demodSig = pskdemod(rxSig,M,pi/4,... 'OutputType','approxllr','NoiseVariance',noiseVariance); % Decode and update number of bit errors % Using bp rxBits1 = ldpcDecode(demodSig,decoderCfg1,maxNumIter); numErr1 = biterr(data,rxBits1); % Using norm-min-sum rxBits2 = ldpcDecode(demodSig,decoderCfg2,maxNumIter); numErr2 = biterr(data,rxBits2); ttlErr = ttlErr + [numErr1 numErr2]; end ttlBits = numCalls*numel(rxBits1); errRate(ii,:) = ttlErr/ttlBits; end
Compare Bit Error Rates
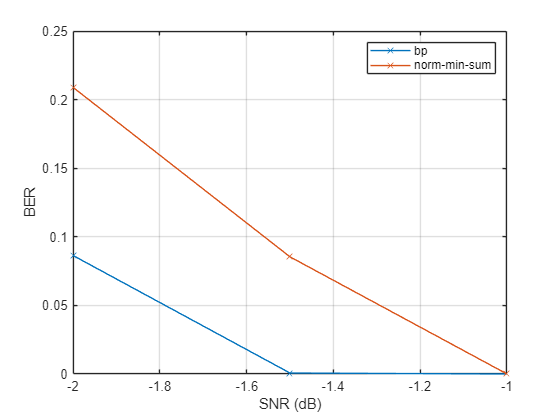
Plot the error statistics. The belief propagation algorithm is expected to achieve a slightly lower bit error rate than the normalized min-sum algorithm.
plot(snr,errRate,'-x') grid on legend('bp','norm-min-sum') xlabel('SNR (dB)') ylabel('BER')
Compare Speeds
Compare the execution speeds of four cases. By default, ldpcDecode terminates decoding when all parity checks are satisfied.
% Use belief propagation algorithm on CPU, without multithreading demodSigCPU = gather(demodSig); tic [rxBitsCPU1,actualNumIterCPU1,finalParityChecksCPU1] = ... ldpcDecode(demodSigCPU,decoderCfg1,maxNumIter,'Multithreaded',false); toc
Elapsed time is 4.270400 seconds.
% Use belief propagation algorithm on CPU, with multithreading tic [rxBitsCPU2,actualNumIterCPU2,finalParityChecksCPU2] = ... ldpcDecode(demodSigCPU,decoderCfg1,maxNumIter); toc
Elapsed time is 1.069500 seconds.
% Use belief propagation algorithm on GPU tic [rxBits1,actualNumIter1,finalParityChecks1] = ... ldpcDecode(demodSig,decoderCfg1,maxNumIter); toc
Elapsed time is 2.117112 seconds.
% Use normalized min-sum algorithm on GPU tic [rxBits2,actualNumIter2,finalParityChecks2] = ... ldpcDecode(demodSig,decoderCfg2,maxNumIter); toc
Elapsed time is 0.615488 seconds.
Examine Optional Decoder Outputs
Confirm that the normalized min-sum algorithm needs fewer iterations than the belief propagation algorithm when the SNR is sufficiently high.
length(find(actualNumIter2 < actualNumIter1))
ans = 50
length(find(actualNumIter2 == actualNumIter1))
ans = 0
Confirm that the final parity checks are all zeros when the actual number of iterations executed is less than the maximum number of iterations specified.
nnz(finalParityChecks1(:,actualNumIter1<maxNumIter))
ans = 0
nnz(finalParityChecks2(:,actualNumIter2<maxNumIter))
ans = 0
Restore the state for random number generation.
rng(s);
Input Arguments
Log-likelihood ratios, specified as a matrix with the number of rows equal to the
BlockLength property of the input decodercfg.
Each column of llr corresponds to a codeword. The function decodes
each column independently. A positive LLR indicates that the corresponding bit is more
likely a zero.
Data Types: double | single
LDPC decoder configuration, specified as an ldpcDecoderConfig object.
Maximum number of decoding iterations, specified as a positive scalar.
Data Types: double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: Termination='max'
Output format, specified as one of these values:
'info'— Output only the decoded information bits. The number of rows that the function outputs equals theNumInformationBitsproperty for the inputdecodercfg.'whole'— Output all of the decoded LDPC codeword bits, including information bits and parity-check bits. The number of rows that the function outputs equals theBlockLengthproperty for the inputdecodercfg.
Decision type for LDPC decoding, specified as one of these values:
'hard'— Perform hard-decision decoding and output decoded bits as values ofint8data type.'soft'— Perform soft-decision decoding and output LLRs with the same data type as the input.
Scaling factor for the normalized min-sum decoding algorithm, specified as a scalar in the range (0, 1]. For more information, see Normalized Min-Sum Decoding.
Dependencies
To enable this property, set the Algorithm property of the
input decodercfg to 'norm-min-sum'.
Offset for the min-sum decoding algorithm, specified as a scalar. For more information, see Offset Min-Sum Decoding.
Dependencies
To enable this property, set the Algorithm property of the
input decodercfg to 'offset-min-sum'.
Decoding termination criteria, specified as one of these values:
'early'— Terminate decoding iterations when all of the parity checks are satisfied, up to a maximum number of iterations specified by inputmaxnumiter.'max'— Terminate decoding when the maximum number of iterations,maxnumiter, are complete.
Enable multithreaded execution on the CPU, specified as a logical
1 (true) or 0
(false). When you run MATLAB® in interpreted mode and set this argument to true,
the function executes the decoding algorithm with multiple threads. The function turns
off multithreaded execution when NumRowsPerLayer = 1 in the input
decodercfg
object.
Tip
For large parity-check matrices, multithreaded execution significantly reduces the processing time for LDPC decoding.
Dependencies
To enable this property, run MATLAB on the CPU in interpreted mode.
Output Arguments
Decoded codewords, returned as a matrix with K rows that
represent the decoded bits for llr(1:K,:). K equals the
NumInformationBits property of the input decodercfg.
For the decoding operation, each column of llr corresponds to a
codeword. The function decodes each column independently. The OutputFormat
name-value argument specifies whether the output contains decoded information bits
(default) or whole LDPC codeword bits. The DecisionType
name-value argument specifies and determines the decoding decision type and the data
type of this output.
For more information, see Algorithms.
Data Types: int8 | double | single
Actual number of decoding iterations, returned as a row vector. If all of the parity
checks for a codeword are satisfied, decoding can stop before the maximum number of
iterations, maxnumiter,
is reached. This output is a row vector of the actual number of iterations that the
function executes for the codewords.
Data Types: double
Final parity checks for each codeword, returned as a matrix with the number of rows
equal to the ParityCheckBits property of input decodercfg.
For the decoding operation, each column of this output is the final parity checks for
the corresponding codeword.
Data Types: double
Algorithms
LDPC decoding using one of these message-passing algorithms.
The implementation of the belief propagation algorithm is based on the decoding algorithm presented by Gallager [2].

For transmitted LDPC-encoded codeword c = c0, c1, …, cn-1, the input to the LDPC decoder is the log-likelihood ratio (LLR) value .
In each iteration, the key components of the algorithm are updated based on these equations:
,
, initialized as before the first iteration, and
.
At the end of each iteration, L(Qi) contains the updated estimate of the LLR value for transmitted bit ci. The value L(Qi) is the soft-decision output for ci. If L(Qi) ≤ 0, the hard-decision output for ci is 1. Otherwise, the hard-decision output for ci is 0.
If decoding is configured to stop when all of the parity checks are satisfied, the algorithm verifies the parity-check equation (H c' = 0) at the end of each iteration. When all of the parity checks are satisfied, or if the maximum number of iterations is reached, decoding stops.
Index sets and are based on the parity-check matrix (PCM). Index sets Ci and Vj correspond to all nonzero elements in column i and row j of the PCM, respectively.
This figure shows the computation of these index sets in a given PCM for i = 5 and j = 3.

To avoid infinite numbers in the algorithm equations, atanh(1) and atanh(–1) are set to 19.07 and –19.07, respectively. Due to finite precision, MATLAB returns 1 for tanh(19.07) and –1 for tanh(-19.07).
The implementation of the layered belief propagation algorithm is based on the decoding algorithm presented in Hocevar [3], Section II.A. The decoding loop iterates over subsets of rows (layers) of the PCM. For each row, m, in a layer and each bit index, j, the implementation updates the key components of the algorithm based on these equations:
(1) ,
(2) ,
(3) ,
(4) , and
(5) .
For each layer, the decoding equation (5) works on the combined input obtained from the current LLR inputs and the previous layer updates .
Because only a subset of the nodes is updated in a layer, the layered belief propagation algorithm is faster compared to the belief propagation algorithm. To achieve the same error rate as attained with belief propagation decoding, use half the number of decoding iterations when you use the layered belief propagation algorithm.
The implementation of the normalized min-sum decoding algorithm follows the layered belief propagation algorithm with equation (2) replaced by
,
where α is in the range (0, 1] and is the scaling factor specified by the
MinSumScalingFactor input argument to the ldpcDecode function. This equation is an adaptation of equation (4)
presented in Chen [4].
The implementation of the offset min-sum decoding algorithm follows the layered belief propagation algorithm with equation (2) replaced by
,
where β ≥ 0 and is the offset specified by the
MinSumOffset input argument to the ldpcDecode function. This equation is an adaptation of equation (5)
presented in Chen [4].
References
[1] IEEE® Std 802.11™-2020 (Revision of IEEE Std 802.11-2016). "Part 11: Wireless LAN Medium Access Control (MAC) and Physical Layer (PHY) Specifications." IEEE Standard for Information technology — Telecommunications and information exchange between systems. Local and metropolitan area networks — Specific requirements.
[2] Gallager, Robert G. Low-Density Parity-Check Codes. Cambridge, MA: MIT Press, 1963.
[3] Hocevar, D.E. "A reduced complexity decoder architecture via layered decoding of LDPC codes." In IEEE Workshop on Signal Processing Systems, 2004. SIPS 2004, 107-112. https://doi.org/10.1109/SIPS.2004.1363033.
[4] Chen, Jinghu, R.M. Tanner, C. Jones, and Yan Li. "Improved min-sum decoding algorithms for irregular LDPC codes." In Proceedings. International Symposium on Information Theory, 2005. ISIT 2005. https://doi.org/10.1109/ISIT.2005.1523374.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using MATLAB® Coder™.
This function supports GPU array inputs. For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Note
Soft-decision outputs for BP and layered BP decoding algorithms may vary by a small amount when compared across CPU and GPU processors. This difference arises from the order of the numerical operations on the two processors. System-level metrics, such as bit error rate, will converge after sufficient signal samples have been processed.
Version History
Introduced in R2021bThe ldpcDecode function adds support for gpuArray (Parallel Computing Toolbox) object processing to run code on a graphics processing unit (GPU). On a
computer that has a GPU, when the llr input is a
gpuArray, the function outputs Y and finalparitychecks
as gpuArray objects and actualnumiter as
a numeric array on the CPU.
The ldpcDecode function adds support for input of single data type
signals. If the input signal is of type single, then the function natively computes in
single precision, and the returned output is also of type single.
Before R2023b, an input signal with datatype single was cast to
double, and the function natively computed in double precision, and was
cast back to single when output.
Outputs in R2023b may be slightly different when compared to previous releases. Comparing results from R2023b and previous releases may show slight differences due to the rounding of native single precision versus double precision computations.
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)