OptimizerTRSADEA
Description
Use the OptimizerTRSADEA object to create a TR-SADEA optimizer. Use
the object properties and functions set up and tune the optimizer parameters, and integrate
the TR-SADEA optimizer as a black box into your workflow using a function
handle.
You can use the TR-SADEA optimizer for high-dimensional (with 30 or more design variables), highly nonlinear problems where focused local search and adaptive refinement is necessary. It is particularly effective for applications such as optimizing large-scale antenna arrays (phased arrays, MIMO antennas, or reconfigurable metasurfaces), high-fidelity EM simulations with many constraints, and fine-tuning near an optimal design.
The TR-SADEA optimizer aims to find a local minimum of the objective function across several design variables within a bounded domain. For more information, see optimization algorithms.
Creation
Description
s = OptimizerTRSADEA(bounds)bounds.
s = OptimizerTRSADEA(bounds,PropertyName=Value)PropertyName is the property
name and Value is the corresponding value. You can specify the
name-value arguments in any order as
PropertyName1=Value1,...,PropertyNameN=ValueN. Properties that you
do not specify retain their default values.
For example, s = OptimizerTRSADEA([1;3],UseParallel=1) creates a
TR-SADEA optimizer object with a single design variable with a lower bound of 1 and
upper bound of 3 and uses a parallel pool for optimization.
Input Arguments
Properties
Object Functions
checkExitCondition | Check exit status of optimizer |
defineInitialPopulation | Set initial population size |
getBestMemberData | View best member data after optimization |
getInitializationData | View optimizer member data at initialization |
getIterationData | View optimization data for completed iterations |
getNumberOfEvaluations | Get number of function evaluations performed |
isConverged | Check convergence status of optimizer |
isFunctionEvaluationsExhausted | Check function evaluations completion status |
optimize | Optimize custom evaluation function using specified parameters |
optimizeWithPlots | Optimize custom evaluation function and plot population density and convergence |
performRestore | Restore optimizer parameters to values from the previous successful iteration |
setMaxFunctionEvaluations | Set upper limit for number of function evaluations |
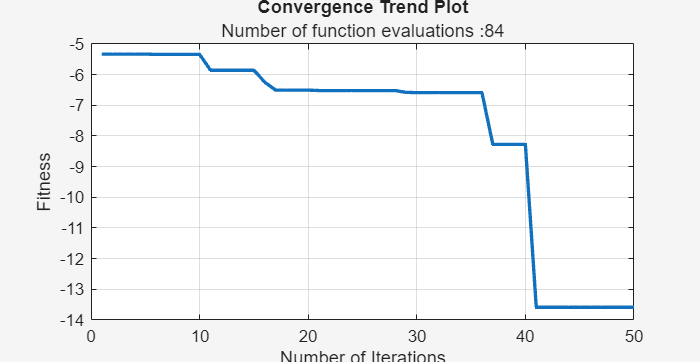
showConvergenceTrend | Plot optimization convergence trend |
Examples
Version History
Introduced in R2025a