Compute Thrust and Torque Coefficients Using Rotor Block
This example shows how to use the Rotor block in Aerospace Blockset™ to compute the thrust and torque coefficients for an isolated rotor. In this example, you compare the results of this computation with the values you obtain using blade element momentum theory (BEMT) and, where available, experimental results from literature [1]. This example considers the variation of lift and drag coefficient with angle of attack, and the effect of profile drag in the BEMT computation.
In the BEMT computation, the fsolve (Optimization Toolbox) function in Optimization Toolbox™ is used to solve for the average inflow through the rotor disc.
Rotor Model
The rotor model in this example is taken from [2]. These parameters are saved in the Ref1Nb2Data.mat file as the structure array rotorParams:
Nb:Number of blades in the rotorR:Radius of the blade, in meterse:Blade hinge-offset, in meters, measured from center of rotationrc:Root cutout, in metersc:Blade chord, in metersrpm:Rotor revolutions per minute (rpm)a: Blade section lift curve slope, in per radiancd0:Mean drag coefficient for the blade airfoil
The root cutout is the inboard region of the blade where the rotor hub, hinges, and bearings are attached. This region has a high drag coefficient and does not contribute to the lift.
Load the Ref1Nb2Data.mat file to add these parameters to the workspace.
refData = load('Ref1Nb2Data.mat'); Nb = refData.rotorParams.Nb; radius = refData.rotorParams.R; hingeOffset = refData.rotorParams.e; rootCutout = refData.rotorParams.rc; chord = refData.rotorParams.c; OmegaRPM = refData.rotorParams.rpm; Omega = convangvel(OmegaRPM, 'rpm' ,'rad/s'); sigma = Nb*chord/pi/radius; % rotor solidity clalpha = refData.rotorParams.a; cd0 = refData.rotorParams.cd0;
Convert the reference rotor rotational velocity in rpm to rad/s using the convangvel function in Aerospace Toolbox. The rotor solidity is the ratio of the blade area ( for constant chord blades) to the rotor disc area ().
The lift and drag coefficient data [2] corresponding to the NACA0015 blade airfoil is saved in the NACA0015Data.mat file.
The file contains this data:
theta_NACA0015: Array of angle of attack values, in degrees, at which lift and drag coefficient data is availableCL_NACA0015: Array of lift coefficient valuesCD_NACA0015: Array of drag coefficient values
Load the data in the NACA0015Data.mat file.
airfoilData = load('NACA0015data.mat');Blade Element Momentum Theory (BEMT)
Blade element momentum theory combines the simple momentum theory (SMT) and the blade element theory (BET) [1].
Simple Momentum Theory
In SMT, the rotor is an actuator disc that can support a pressure difference and accelerate the air through the disc. This theory is based on basic conservation laws of fluid mechanics.
Using this theory, the rotor thrust () is related to the induced velocity () at the rotor disc by this equation
,
where is the density of air and is the rotor disc area ().
Blade Element Theory
In BET, the blade is divided into airfoil sections capable of generating aerodynamic forces. This figure shows the blade section aerodynamics.
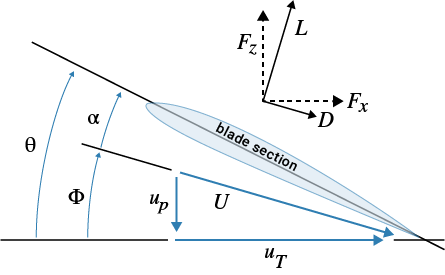
The variables in the diagram are
: pitch angle of blade
: inflow angle
: aerodynamic angle of attack
: lift force at the blade section
: drag force at the blade section
: net force perpendicular to the disc plane
: net force tangential to the disc plane
: perpendicular air velocity seen by the blade
: tangential air velocity seen by the blade
: resultant velocity
where
.
The sectional lift and drag forces are defined as
,
where is the air density. and are the sectional lift and drag coefficients and are typically functions of the angle of attack, Mach number, and other parameters. In this example, the coefficients are functions of angle of attack alone (based on the available airfoil data).
The aerodynamic forces perpendicular and parallel to the disc plane are defined as
.
In hover, , the induced velocity, and , where is the rotational velocity of the rotor and is the dimensional radial location. The non-dimensional radial location is represented by .
You can apply small angle approximations [1] to obtain
.
Here, is the non-dimensional induced velocity or inflow ratio.
The elemental thrust and torque can now be defined as
.
Remove the dimensions of the quantities to obtain the thrust and torque coefficients:
Combining Momentum and Blade Element Theories
Considering a rotor in hover, based on differential momentum theory, the incremental thrust for a rotor annulus of width at radial position is
.
The corresponding non-dimensional thrust coefficient is
.
To account for the blade tip-loss effects, the Prandtl tip loss function[2] can be included as
,
where .
Based on BET, the incremental thrust coefficient for the annulus is
.
The incremental torque coefficient is
.
Since the lift and drag coefficients depend on the local angle of attack, , using interpolation on the available reference data, the coefficient values can be obtained at the required .
The angle of attack is computed as
.
Here, is the blade pitch angle at a radial location and depends on the blade twist and the pitch input. The reference blade considered in this example is untwisted, and as pitch input, only the collective pitch () variation is considered.
Hence, you have
.
Considering the two equations for incremental thrust coefficient, you get
.
Solving the above equation at each radial location , you can compute the non-dimensional induced velocity () at the point. Use this value to compute the thrust and torque coefficients.
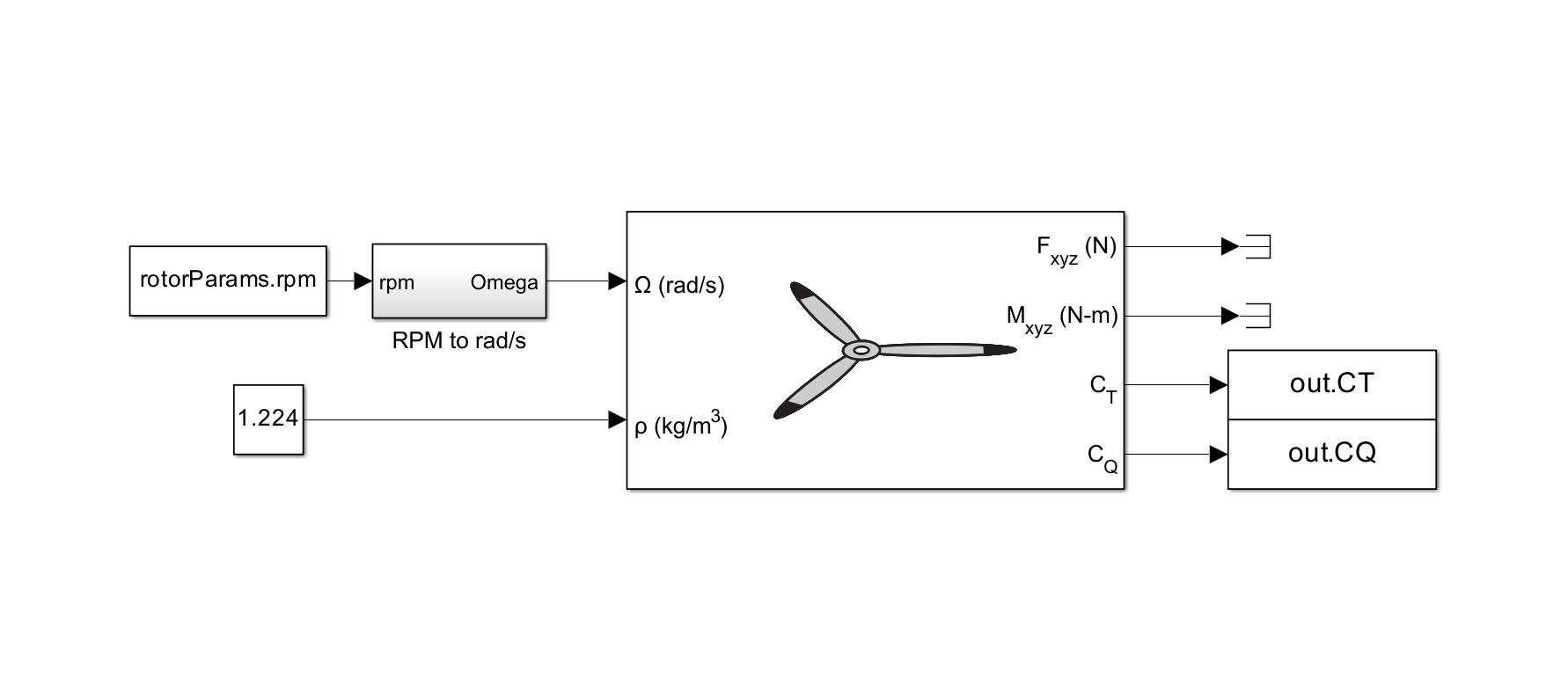
Rotor Block
You can use the Rotor block in Aerospace Blockset to compute the aerodynamic forces and moments in all three dimensions for an isolated rotor or propeller. This computation requires the aerodynamic and mechanical parameters of the rotor, including the thrust and torque coefficients, as inputs. You can obtain these coefficients experimentally by doing a static thrust and torque analysis. This approach is typical for small propellers used in multirotor vehicles like quadrotors. In scenarios where the experimental study is not possible, or you want to compare the experimentally obtained values and theoretical values, you can use the Rotor block for the computation. The 'CT and CQ Source' parameter is set to 'Compute using BEMT' such that the block computes the CT and CQ values based on the provided inputs.
The Rotor block assumes:
Constant chord along the blade span
Constant lift curve slope
Approximate profile drag computation
Only linear, or ideal, twist distribution
Variation of Thrust and Torque Coefficients with Collective Pitch Input
Compute the values of and corresponding to different values of collective pitch input . Based on reference data, the range of collective pitch inputs considered is from to .
theta0Array = 0:12;
These matrices are used to save the thrust and torque coefficient results obtained using the two approaches. For BEMT computation, the torque coefficient values are computed with and without the inclusion of profile drag component. Save the values in the two columns of the CQArrayBEMT matrix.
CTArrayBEMT = zeros(length(theta0Array),1); CQArrayBEMT = zeros(length(theta0Array),2); CTArrayRotor = zeros(length(theta0Array),1); CQArrayRotor = zeros(length(theta0Array),1);
Computation Using BEMT
Compute net thrust and torque coefficients using BEMT by calculating the incremental values of the coefficients at each radial location and then summing them.
Nelements = 100; % number of radial elements xnodes = linspace((rootCutout-hingeOffset)/(radius-hingeOffset),1,Nelements+1); % radial locations delr = diff(xnodes); % corresponding to deltar in equations
Compute the lift and drag coefficients and at each radial location, using the function handles 'computeCl' and 'computeCd', with alpha () as the input argument.
computeCl=@(alpha)interp1(airfoilData.theta_NACA0015, airfoilData.CL_NACA0015, convang(alpha,'rad','deg')); computeCd=@(alpha)interp1(airfoilData.theta_NACA0015, airfoilData.CD_NACA0015, convang(alpha,'rad','deg'));
Compute the angle of attack at each radial location and convert to degrees using the convang function in Aerospace Toolbox. For interpolation, use the MATLAB® function interp1.
To incorporate tip loss, implement the Prandtl tip loss function as a function handle with the non-dimensional radial location and the inflow () as input arguments.
F = @(r,lambda)(2/pi)*acos(exp(-.5*Nb*((1-r)/(r*(lambda/r)))));
To solve for at each radial location, use the fsolve (Optimization Toolbox) function in Optimization Toolbox. The default 'trust-region-dogleg' algorithm is used to solve the equation. Set the initial guess for the fsolve function using the initInflow variable.
initInflow = 0.01; opts = optimset('Display','off');
Compute the net thrust and torque coefficients by looping over the range of collective pitch values and the number of radial locations for each pitch input.
Use the convang function to convert the collective pitch angle to radians. Compute the torque coefficient two ways, with and without the profile drag component.
for thetaInd = 1:length(theta0Array) % loop for collective pitch input theta0 = convang(theta0Array(thetaInd),'deg','rad'); CT = 0; % initializing CT % initializing CQ CQwithDrag = 0; % with profile drag effect included CQwithoutDrag = 0; % without profile drag for rInd = 1:Nelements-1 % loop for radial locations r =xnodes(rInd)+delr(rInd)/2; % solving for lambda at r lambdaVal = fsolve(@(lambda)4*F(r,lambda)*lambda^2*r-.5*sigma*r^2*(computeCl(theta0 - (lambda/r))),initInflow, opts); % computing incremental thrust coefficient dCT = 4*F(r,lambdaVal)*lambdaVal^2*r*delr(rInd); CT = CT + dCT; CQwithDrag = CQwithDrag + lambdaVal*dCT+ 0.5*sigma*computeCd(theta0 - (lambdaVal/r))*r^3*delr(rInd); CQwithoutDrag = CQwithoutDrag + lambdaVal*dCT; end CTArrayBEMT(thetaInd) = CT; CQArrayBEMT(thetaInd,1) = CQwithDrag; CQArrayBEMT(thetaInd,2) = CQwithoutDrag; end
Computation Using Rotor Block
To compute the thrust and torque coefficients using Rotor block in the Aerospace blockset, use the Simulink® model, CTCQcomputation.slx.
The Model Callbacks function adds the reference parameters to the model.
The mask parameters
R(radius),c(chord),e(hinge offset),clalpha(lift curve slope), and cd0 (mean drag coefficient) are set to the reference values.The twist type is set to linear with the root pitch angle () set to the collective pitch angle (
theta0).The input parameter to the block, density (), is set to the approximate sea-level value of , and rotor speed () is set using the reference data (rpm).
To loop over the varying collective pitch angles, use a Simulink.SimulationInput object.
model = 'CTCQcomputation'; open_system(model); simin(1:length(theta0Array)) = Simulink.SimulationInput(model); for i = 1:length(theta0Array) theta0 = convang(theta0Array(i),'deg','rad'); simin(i) = simin(i).setVariable('theta0',theta0); end simout = sim(simin,'ShowProgress','off');% turning off simulation progress messages for i = 1:length(theta0Array) CTArrayRotor(i) = simout(1,i).CT; CQArrayRotor(i) = simout(1,i).CQ; end
Note: You can include pitch inputs in the Rotor block through optional input ports, enabled using the 'Include pitch angle inputs' checkbox. Setting 'CT and CQ Source' to 'Compute using BEMT' along with enabling the 'Include pitch angle inputs' checkbox will activate the collective pitch input () port. You can directly provide the collective pitch variation considered in this analysis as an input to the port.
Analyzing Results
The experimental results for thrust and torque coefficients are obtained from [1] and saved in the Ref1Nb2Data.mat file. The experimental results in the file are:
theta_data: Collective pitch angles at which data is availableCTdata: Thrust coefficient dataCQdata: Torque coefficient data
Variation of Thrust Coefficient with Collective Pitch
Plot the variation of with .
figure,plot(theta0Array,CTArrayBEMT,'b',... theta0Array, CTArrayRotor, 'r',refData.theta_data, refData.CTdata, 'k*') ylim([0 0.01]); xlabel('\theta_0') ylabel('C_T') ax = gca; ax.YRuler.Exponent = 0; % setting y-axis ticks to standard notation title('Variation of C_T with \theta_0') legend('BEMT','Rotor Block', 'Experiment',... 'Location','best','NumColumns',1);
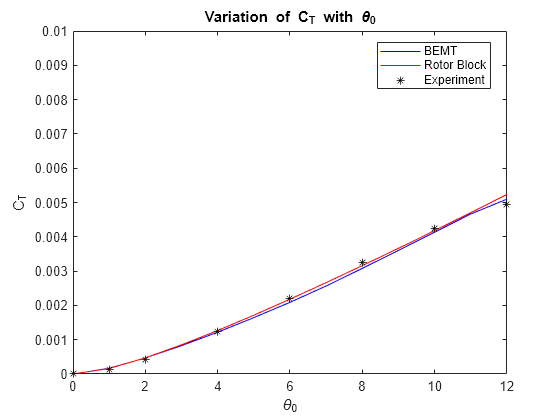
The experimental results, the results obtained using BEMT, and the computed values obtained using Rotor block correlate well. Even though the computation using Rotor block assumes a constant value for the lift coefficient, the effect of varying lift coefficient along the span (with angle of attack) is minimal.
Variation of Torque Coefficient with Collective Pitch
Plot the variation of with .
figure,plot(theta0Array,CQArrayBEMT(:,1),'b', theta0Array,CQArrayRotor,'r',... refData.theta_data, refData.CQdata, 'k*') xlabel('\theta_0') ylabel('C_Q') ylim([0 0.0006]); title('Variation of C_Q with \theta_0') ax = gca; ax.YRuler.Exponent = 0; legend('BEMT with profile drag', 'Rotor Block', 'Experiment',... 'Location','best','NumColumns',1);

The results obtained using BEMT with profile drag match reasonably well with the experimental results. The results obtained using Rotor block correlate well with the experimental and BEMT results for low values of collective pitch input. The deviation increases with increasing collective pitch input, which indicates of the effect of varying drag coefficient (with angle of attack).
In Rotor block, the profile drag component is included in torque computation as an approximation.
For small values of , the profile drag contribution over the entire rotor can be roughly approximated as
.
Here, is the mean drag coefficient.
Consider the approximate value of for the NACA0015 blade airfoil [2] in computing the profile drag component. Add the result to torque coefficient values obtained using BEMT without profile drag and compare with the BEMT with profile drag and Rotor block values.
CQprofileApprox = sigma*cd0/8; CQprofileApproxBEMT = CQArrayBEMT(:,2)+CQprofileApprox; figure,plot(theta0Array,CQArrayBEMT(:,1),'b', theta0Array,CQprofileApproxBEMT(:,1),'--b', ... theta0Array, CQArrayRotor,'r') xlabel('\theta_0') ylabel('C_Q') ylim([0 0.0005]); title('Variation of C_Q with \theta_0') ax = gca; ax.YRuler.Exponent = 0; legend('BEMT with profile drag', 'BEMT with approximate profile drag', 'Rotor Block',... 'Location', 'best', 'NumColumns', 1);
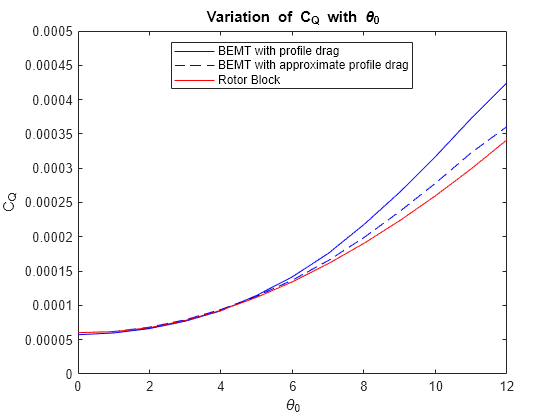
The results indicate the difference between the experimental values and Rotor block values observed at higher collective inputs is primarily due to the approximation used in the profile drag computation. The variation in drag coefficient with angle of attack is not considered in the Rotor block.
The analysis shows that for the specific rotor:
The approximation works well for smaller pitch input values, as would be the case for smaller rotors or propellers.
The effect of varying lift and drag coefficient values along the span on the computed torque coefficient is small.
Conclusion
The analysis shows that Rotor block can be used for the computation of thrust and torque coefficient values, with limitations.
Constant chord: In case of rotors with varying chord, computing the mean geometric chord [3] and using it in the computation is a reasonable approximation.
Constant lift coefficient: As the analysis shows, using the mean lift coefficient corresponding to the airfoil in the computation is a good approximation.
Profile drag approximation: The block considers the profile drag contribution through an approximation which provides good correlation for low values of collective pitch.
Linear or ideal twist distribution: The block can consider only linear or ideal twist variations along the span.
References
[1] Johnson, Wayne. Rotorcraft Aeromechanics. Cambridge: Cambridge University Press, 2013.
[2] Knight, Montgomery, and A. Hefner, Ralph. “Static Thrust Analysis of the Lifting Airscrew.” National Advisory Committee on Aeronautics, Technical Note 626. December 1, 1937. NASA Technical Reports Server.
https://ntrs.nasa.gov/api/citations/19930081433/downloads/19930081433.pdf.
[3] Leishman, J. Gordon. Principles of Helicopter Aerodynamics. Cambridge, UK: Cambridge University Press, 2017.