wavefun2
Wavelet and scaling functions 2-D
Syntax
Description
[
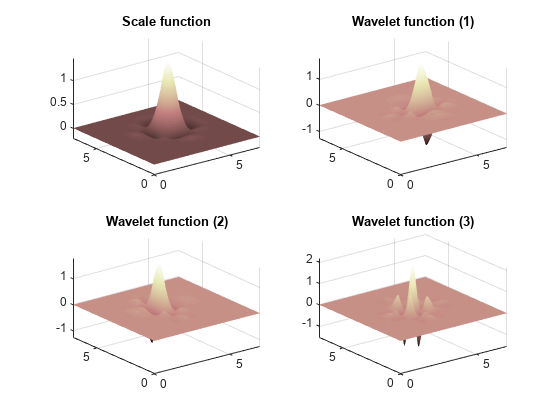
returns an approximation s,w1,w2,w3,xyval] = wavefun2(wname,iter)s of the 2-D scaling function and
approximations w1, w2, and
w3 of the three 2-D wavelet functions associated with the
orthogonal wavelet wname. xyval is a 2-D
grid of points. The positive integer iter specifies the number
of iterations.
The approximations are the tensor products of the one-dimensional scaling and
wavelet functions associated with the orthogonal wavelet wname.
For more information, see Algorithms.
Examples
Input Arguments
Output Arguments
Algorithms
The wavefun2 function returns approximations of the 2-D scaling
function and the three 2-D wavelet functions resulting from the tensor products of the
one-dimensional scaling and wavelet functions associated with the orthogonal wavelet
wname.
If [phi,psi,xval] =
wavefun(, then:wname,iter)
For more information, see wavefun.
References
[1] Daubechies, I. Ten Lectures on Wavelets. CBMS-NSF Regional Conference Series in Applied Mathematics. Philadelphia, PA: Society for Industrial and Applied Mathematics, 1992.
[2] Strang, G., and T. Nguyen. Wavelets and Filter Banks. Wellesley, MA: Wellesley-Cambridge Press, 1996.
Version History
Introduced before R2006a