plot
Description
plot( plots a probability density function
(pdf) of the probability distribution object pd)pd. If
pd is created by fitting a probability distribution to the data, the
pdf is superimposed over a histogram of the data.
plot(___, specifies
options using one or more name-value arguments in addition to any of the input argument
combinations in the previous syntaxes. For example, you can indicate whether to plot a
cumulative distribution function (cdf) or a probability plot instead of a pdf.Name=Value)
H = plot(___)
Examples
Generate random data points from a normal distribution with mean 0 and standard deviation 1.
rng("default") % Set the seed for reproducibility.
Fit a normal distribution to the data.
normaldata = normrnd(0,1,100,1);
normalpd = fitdist(normaldata,"Normal")normalpd =
NormalDistribution
Normal distribution
mu = 0.123085 [-0.10756, 0.353731]
sigma = 1.1624 [1.02059, 1.35033]
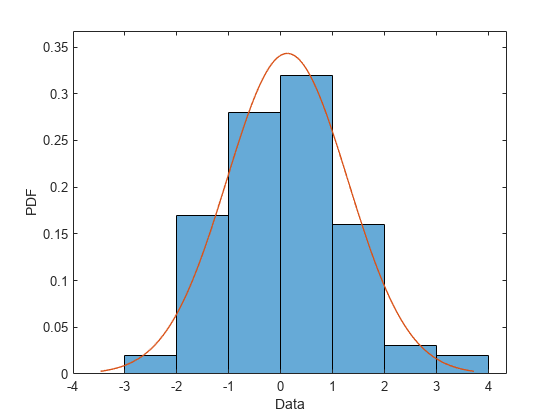
normalpd is a NormalDistribution object that contains the parameter values for the normal distribution fit to the data, and the data. Plot a pdf for the normal distribution with a histogram of the data.
plot(normalpd)
Plot a cdf of the normal distribution fit to the data and a stairs plot of a cdf for the data.
plot(normalpd,PlotType="cdf")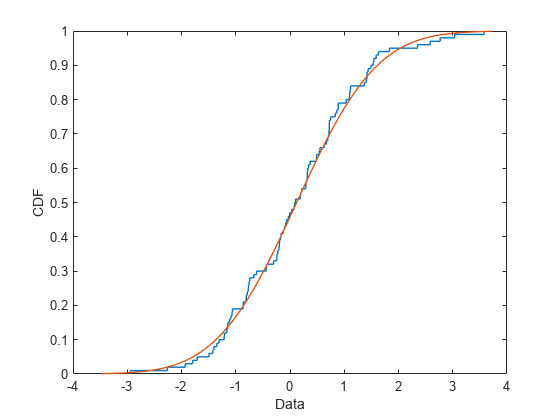
Display a probability plot for the normal distribution fit to the data.
plot(normalpd,PlotType="probability")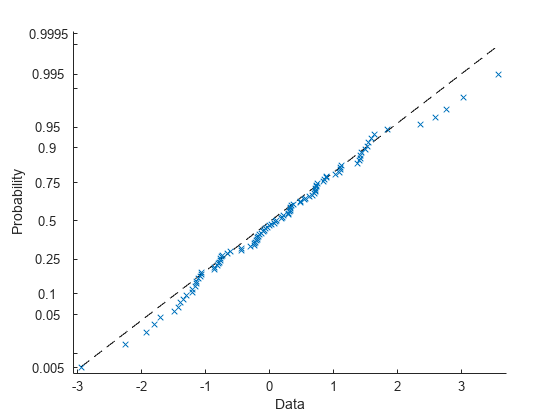
The vertical axis is scaled so that the cdf for the fitted probability distribution is represented by a straight line.
Create a multinomial distribution that has five outcomes with probabilities of 0.1, 0.2, 0.4, 0.2, and 0.1.
multinomialpd = makedist("Multinomial",probabilities=[0.1 0.2 0.4 0.2 0.1])multinomialpd =
MultinomialDistribution
Probabilities:
0.1000 0.2000 0.4000 0.2000 0.1000
Plot a pdf for the multinomial distribution.
plot(multinomialpd)
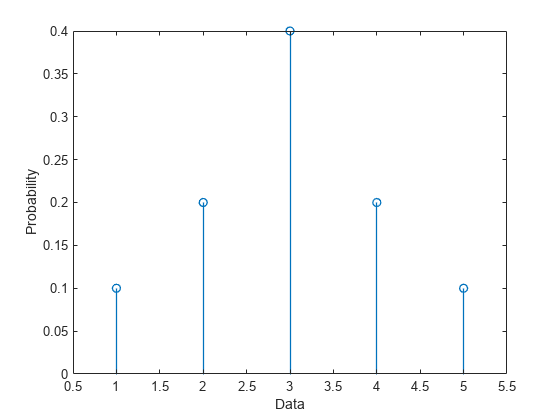
The plot contains a Stem object that represents the probabilities for the data.
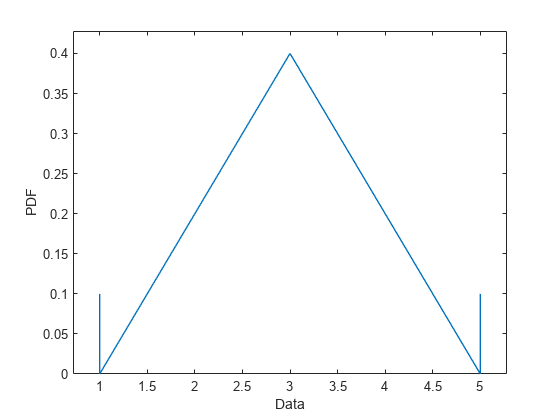
Plot the pdf as a continuous distribution.
plot(multinomialpd,Discrete=0)
Plot the cdf of the fitted multinomial distribution as a stairs plot.
plot(multinomialpd,PlotType="cdf")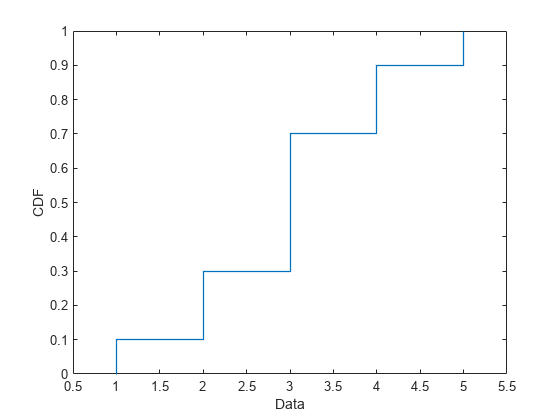
Plot the cdf as a continuous distribution.
plot(multinomialpd,PlotType="cdf",Discrete=0)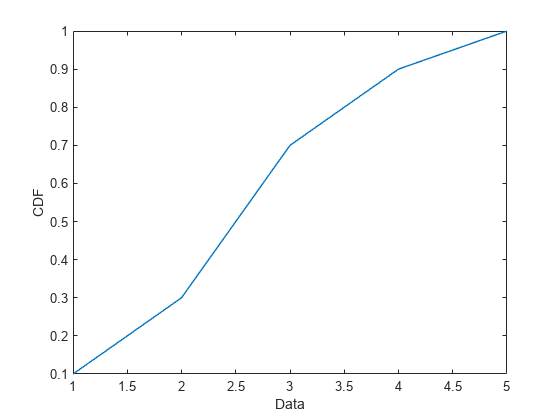
Input Arguments
Probability distribution, specified as one of the probability distribution objects in the following table.
| Distribution Object | Function or App Used to Create Probability Distribution Object |
|---|---|
BetaDistribution | makedist, fitdist, Distribution Fitter |
BinomialDistribution | makedist, fitdist,
Distribution Fitter |
BirnbaumSaundersDistribution | makedist, fitdist,
Distribution Fitter |
BurrDistribution | makedist, fitdist,
Distribution Fitter |
EmpiricalDistribution | fitdist |
ExponentialDistribution | makedist, fitdist,
Distribution Fitter |
ExtremeValueDistribution | makedist, fitdist,
Distribution Fitter |
GammaDistribution | makedist, fitdist,
Distribution Fitter |
GeneralizedExtremeValueDistribution | makedist, fitdist,
Distribution Fitter |
GeneralizedParetoDistribution | makedist, fitdist,
Distribution Fitter |
HalfNormalDistribution | makedist, fitdist,
Distribution Fitter |
InverseGaussianDistribution | makedist, fitdist,
Distribution Fitter |
KernelDistribution | fitdist, Distribution Fitter |
LogisticDistribution | makedist, fitdist,
Distribution Fitter |
LoglogisticDistribution | makedist, fitdist,
Distribution Fitter |
LognormalDistribution | makedist, fitdist,
Distribution Fitter |
LoguniformDistribution | makedist |
MultinomialDistribution | makedist |
NakagamiDistribution | makedist, fitdist,
Distribution Fitter |
NegativeBinomialDistribution | makedist, fitdist,
Distribution Fitter |
NormalDistribution | makedist, fitdist,
Distribution Fitter |
PearsonDistribution | makedist |
PiecewiseLinearDistribution | makedist |
PoissonDistribution | makedist, fitdist,
Distribution Fitter |
RayleighDistribution | makedist, fitdist,
Distribution Fitter |
RicianDistribution | makedist, fitdist,
Distribution Fitter |
StableDistribution | makedist, fitdist,
Distribution Fitter |
tLocationScaleDistribution | makedist, fitdist,
Distribution Fitter |
TriangularDistribution | makedist |
UniformDistribution | makedist |
WeibullDistribution | makedist, fitdist,
Distribution Fitter |
Axes for plot, specified as an Axes graphics object. If you do not
specify the axes by using the ax input argument or the
Parent name-value argument, the plot
function plots into the current axes or creates an Axes object if one
does not exist. For more information on creating an Axes graphics
object, see axes and Axes Properties.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: Discrete=1,PlotType="cdf" plots a cumulative distribution
function (cdf) of the probability distribution as a stairs plot.
Plot type for the probability distribution, specified as one of the following.
"pdf" | Plot the probability density function (pdf). When
pd is fit to data, the pdf is superimposed on a
histogram of the data. |
"cdf" | Plot the cumulative distribution function (cdf). When
pd is fit to data, the cdf is superimposed over an
empirical cdf. |
"probability" | Display a probability plot using a cdf of the data and a cdf of the
fitted probability distribution. This option is available only when
pd is parametric and fit to data. |
Example: PlotType="probability"
Data Types: char | string
Indicator to plot as a discrete function, specified as 1 (true)
or 0 (false). Specify Discrete=0 to display the
pdf or cdf as a line plot. Specify Discrete=1 to display the pdf
as a stem plot or to display the cdf as a stairs plot.
The default value for Discrete is 1 when
pd is a discrete probability distribution object and 0 when
pd is a continuous probability distribution object. If
pd is continuous, plot ignores the
user-specified input for Discrete and plots continuous
functions.
Example: Discrete=0
Data Types: logical
Axes for plot, specified as an Axes graphics object. If you do
not specify the axes by using the ax input argument or the
Parent name-value argument, the
plot function plots into the current axes or creates an
Axes object if one does not exist. For more information on creating
an Axes graphics object, see axes and Axes Properties.
Output Arguments
Handles to the plotted graphics objects, returned as a Line object,
Stem object, Stairs object, or graphics array.
When
PlotTypeis set to"pdf"or"cdf", andpdis not fit to data,His a single handle corresponding to the pdf or cdf for the distribution.When
PlotTypeis set to"pdf"or"cdf", andpdis fit to data,His a 1-by-2 graphics array. The first entry of the graphics array corresponds to the pdf or cdf for the distribution, and the second entry corresponds to the data.When
PlotTypeis set to"probability",His a 2-by-1 graphics array with entries corresponding to the data and the distribution.
The table below shows how the returned graphics object depends on whether the
distribution is discrete, whether pd is fit to data, and the
specified values for the name-value arguments Discrete and
PlotType.
| Distribution Type | Fit to Data | Discrete value | PlotType value | Returned Graphics Object |
|---|---|---|---|---|
| Discrete | No | 1 | "pdf" | Stem |
"cdf" | Stairs | |||
| 0 | "pdf" | Line | ||
"cdf" | Line | |||
| Yes | 1 | "pdf" | [ | |
"cdf" | [ | |||
"probability" | [ | |||
| 0 | "pdf" | [ | ||
"cdf" | [ | |||
"probability" | [ | |||
| Continuous | No | 0 | "pdf" | Line |
"cdf" | Line | |||
| Yes | 0 | "pdf" | [ | |
"cdf" | [ | |||
"probability" | [ |
Version History
Introduced in R2022b
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)