median
Median of probability distribution
Syntax
Description
Examples
Load the sample data. Create a vector containing the first column of students' exam grade data.
load examgrades
x = grades(:,1);Create a normal distribution object by fitting it to the data.
pd = fitdist(x,'Normal')pd =
NormalDistribution
Normal distribution
mu = 75.0083 [73.4321, 76.5846]
sigma = 8.7202 [7.7391, 9.98843]
Compute the median of the fitted distribution.
m = median(pd)
m = 75.0083
For a symmetrical distribution such as the normal distribution, the median is equal to the mean, mu.
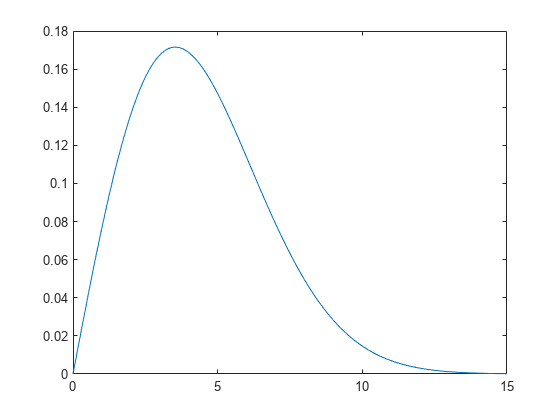
Create a Weibull probability distribution object.
pd = makedist('Weibull','A',5,'B',2)
pd =
WeibullDistribution
Weibull distribution
A = 5
B = 2
Compute the median of the distribution.
m = median(pd)
m = 4.1628
For a skewed distribution such as the Weibull distribution, the median and the mean may not be equal.
Calculate the mean of the Weibull distribution and compare it to the median.
mean = mean(pd)
mean = 4.4311
The mean of the distribution is greater than the median.
Plot the pdf to visualize the distribution.
x = [0:.1:15]; pdf = pdf(pd,x); plot(x,pdf)
Input Arguments
Probability distribution, specified as one of the probability distribution objects in the following table.
| Distribution Object | Function or App Used to Create Probability Distribution Object |
|---|---|
BetaDistribution | makedist, fitdist, Distribution Fitter |
BinomialDistribution | makedist, fitdist,
Distribution Fitter |
BirnbaumSaundersDistribution | makedist, fitdist,
Distribution Fitter |
BurrDistribution | makedist, fitdist,
Distribution Fitter |
EmpiricalDistribution | fitdist |
ExponentialDistribution | makedist, fitdist,
Distribution Fitter |
ExtremeValueDistribution | makedist, fitdist,
Distribution Fitter |
GammaDistribution | makedist, fitdist,
Distribution Fitter |
GeneralizedExtremeValueDistribution | makedist, fitdist,
Distribution Fitter |
GeneralizedParetoDistribution | makedist, fitdist,
Distribution Fitter |
HalfNormalDistribution | makedist, fitdist,
Distribution Fitter |
InverseGaussianDistribution | makedist, fitdist,
Distribution Fitter |
KernelDistribution | fitdist, Distribution Fitter |
LogisticDistribution | makedist, fitdist,
Distribution Fitter |
LoglogisticDistribution | makedist, fitdist,
Distribution Fitter |
LognormalDistribution | makedist, fitdist,
Distribution Fitter |
LoguniformDistribution | makedist |
MultinomialDistribution | makedist |
NakagamiDistribution | makedist, fitdist,
Distribution Fitter |
NegativeBinomialDistribution | makedist, fitdist,
Distribution Fitter |
NormalDistribution | makedist, fitdist,
Distribution Fitter |
PearsonDistribution | makedist |
PiecewiseLinearDistribution | makedist |
PoissonDistribution | makedist, fitdist,
Distribution Fitter |
RayleighDistribution | makedist, fitdist,
Distribution Fitter |
RicianDistribution | makedist, fitdist,
Distribution Fitter |
StableDistribution | makedist, fitdist,
Distribution Fitter |
tLocationScaleDistribution | makedist, fitdist,
Distribution Fitter |
TriangularDistribution | makedist |
UniformDistribution | makedist |
WeibullDistribution | makedist, fitdist,
Distribution Fitter |
Output Arguments
Median of the probability distribution, returned as a scalar value. The
value of m is the 50th percentile of the probability
distribution.
Extended Capabilities
Usage notes and limitations:
The input argument
pdcan be a fitted probability distribution object for beta, exponential, extreme value, lognormal, normal, and Weibull distributions. Createpdby fitting a probability distribution to sample data from thefitdistfunction. For an example, see Code Generation for Probability Distribution Objects.
For more information on code generation, see Introduction to Code Generation and General Code Generation Workflow.
This function fully supports GPU arrays. For more information, see Run MATLAB Functions on a GPU (Parallel Computing Toolbox).
Version History
Introduced in R2013a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)