meanEffectSize
Description
Effect = meanEffectSize(X,Y,Name=Value)
Examples
Load the stock returns data and define the variable for which to compute the mean-difference effect size.
load stockreturns
x = stocks(:,1);Compute the mean-difference effect size of the stock returns compared to the default mean value of 0, and compute the 95% confidence intervals for the effect size.
effect = meanEffectSize(x)
effect=1×2 table
Effect ConfidenceIntervals
________ ______________________
MeanDifference -0.20597 -0.41283 0.00087954
The meanEffectSize function uses the exact method to estimate the confidence intervals when you use the mean-difference effect size.
You can also specify the mean value you want to compare against.
effect = meanEffectSize(x,Mean=-1)
effect=1×2 table
Effect ConfidenceIntervals
_______ ___________________
MeanDifference 0.79403 0.58717 1.0009
Load Fisher's iris data and define the variables for which to compute the median-difference effect size.
load fisheriris species2 = categorical(species); x = meas(species2=='setosa'); y = meas(species2=='virginica');
Compute the median-difference effect size of the observations from two independent samples.
effect = meanEffectSize(x,y,Effect="mediandiff")effect=1×2 table
Effect ConfidenceIntervals
______ ___________________
MedianDifference -1.5 -1.8 -1.3
By default, the meanEffectSize function assumes that the samples are independent (that is, Paired=false). The function uses bootstrapping to estimate the confidence intervals when the effect type is median-difference.
Visualize the median-difference effect size using the Gardner-Altman plot.
gardnerAltmanPlot(x,y,Effect="mediandiff");
The Gardner-Altman plot displays the two data samples on the left. The median of the sample Y corresponds to the zero effect size on the effect size axis, which is the yellow axis line on the right. The median of the sample X corresponds to the value of the effect size on the effect size axis. The plot displays the actual median-difference effect size value and the confidence intervals with the vertical error bar.
Load Fisher's iris data and define the variables for which to compare the Cohen's d effect size.
load fisheriris species2 = categorical(species); x = meas(species2=='setosa'); y = meas(species2=='virginica');
Compute the Cohen's d effect size for the observations from two independent samples, and compute the 95% confidence intervals for the effect size. By default, the meanEffectSize function uses the exact formula based on the noncentral t-distribution to estimate the confidence intervals when the effect size type is Cohen's d. Specify the bootstrapping options as follows:
Set
meanEffectSizeto use bootstrapping for confidence interval computation.Use parallel computing for bootstrapping computations. You need Parallel Computing Toolbox™ for this option.
Use 3000 bootstrap replicas.
rng(123) % For reproducibility effect = meanEffectSize(x,y,Effect="cohen",ConfidenceIntervalType="bootstrap", ... BootstrapOptions=statset(UseParallel=true),NumBootstraps=3000)
effect=1×2 table
Effect ConfidenceIntervals
_______ ___________________
CohensD -3.0536 -3.6232 -2.4073
Visualize the Cohen's d effect size using the Gardner-Altman plot with the same options set.
gardnerAltmanPlot(x,y,Effect="cohen",ConfidenceIntervalType="bootstrap", ... BootstrapOptions=statset(UseParallel=true),NumBootstraps=3000);
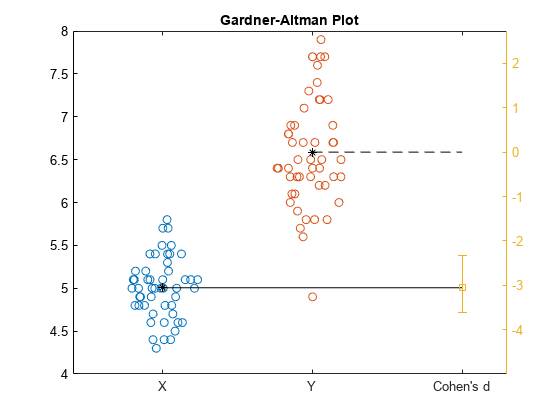
The Gardner-Altman plot displays the two data samples on the left. The mean of the sample Y corresponds to the zero effect size on the effect size axis, which is the yellow axis line on the right. The mean of the sample X corresponds to the value of the effect size on the effect size axis. The plot displays the Cohen's d effect size value and the confidence intervals with the vertical error bar.
Load exam grades data and define the variables to compare.
load examgrades
x = grades(:,1);
y = grades(:,2);Compute the mean-difference effect size of the grades from the paired samples, and compute the 95% confidence intervals for the effect size.
effect = meanEffectSize(x,y,Paired=true)
effect=1×2 table
Effect ConfidenceIntervals
________ ___________________
MeanDifference 0.016667 -1.3311 1.3644
The meanEffectSize function uses the exact method to estimate the confidence intervals when you use the mean-difference effect size.
You can specify a different effect size type. (Note that you cannot use Glass's delta for paired samples.) Use robust Cohen's d to compare the paired sample means. Compute the 97% confidence intervals for the effect size.
effect = meanEffectSize(x,y,Paired=true,Effect="robustcohen",Alpha=0.03)effect=1×2 table
Effect ConfidenceIntervals
________ ___________________
RobustCohensD 0.059128 -0.1405 0.26573
The meanEffectSize function uses bootstrapping to estimate the confidence intervals when the effect size type is robust Cohen's d.
Visualize the effect size using the Gardner-Altman plot. Specify robust Cohen's d as the effect size, and compute the 97% confidence intervals.
gardnerAltmanPlot(x,y,Paired=true,Effect="robustcohen",Alpha=0.03);
The Gardner-Altman plot displays the paired data on the left. The blue lines show the values that are increasing and the red lines show the values that are decreasing from the first sample to the corresponding values in the paired sample, respectively. Right side of the plot displays the robust Cohen's d effect size with the 97% confidence interval.
Input Arguments
Input data, specified as a numeric vector.
Data Types: single | double
Input data, specified as a numeric vector.
Data Types: single | double
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: Effect="cliff",Alpha=0.03,ConfidenceIntervalType="bootstrap",VarianceType=unequal
specifies to use the Cliff's Delta effect size, compute the 97% confidence intervals using
bootstrapping, and assume the samples come from populations with unequal
variances.
Confidence level of the confidence intervals for the effect size, specified as a numeric value from 0 to 1. Default value of 0.05 corresponds to the 95% confidence level.
Example: Alpha=0.025
Data Types: single | double
Options for computing bootstrap confidence intervals in parallel, specified as a
structure generated by using statset("bootci").
meanEffectSize uses the following fields.
| Field | Description |
|---|---|
Streams | A
In this case, use a cell array the
same size as the parallel pool. If a parallel pool is not open,
then |
UseParallel | The default is false, indicating serial
computation. |
UseSubstreams | Set to true to compute in a reproducible
fashion. The default is false. To compute
reproducibly, set Streams to a type allowing
substreams: "mlfg6331_64" or
"mrg32k3a". |
Computing bootstrap confidence intervals in parallel requires Parallel Computing Toolbox™.
Example: BootstrapOptions=options
Data Types: struct
Type of confidence interval to compute, specified as "exact",
"bootstrap", or "none". The default value is
"exact" when there is an exact formula for the effect size or
"bootstrap" otherwise. Specify "none" is when
you do not want to compute any confidence intervals.
The default value is "exact" for Cliff's Delta, Glass's delta,
mean-difference, and Cohen's d and "bootstrap" for Kolmogorov-Smirnov
statistic, median-difference, and robust Cohen's d. If you specify confidence interval
type as "exact" for Kolmogorov-Smirnov statistic, median-difference,
and robust Cohen's d, meanEffectSize returns an error.
Example: ConfidenceIntervalType="none"
Data Types: string | char
Effect size type to compute, specified as one of or a cell array of the following built-in options.
Options for single-sample input
| Effect size option | Definition |
|---|---|
"cohen" | Cohen's d for single-sample input. |
"meandiff" | Mean difference. |
"robustcohen" | Robust Cohen's d for single-sample input. |
Options for two-sample input
| Option | Definition |
|---|---|
"cohen" | Cohen's d for two-sample input |
"cliff" | Cliff's Delta |
"glass" | Glass's delta; not supported by |
"kstest" | Kolmogorov-Smirnov statistic |
"mediandiff" | Median difference |
"meandiff" | Mean difference |
"robustcohen" | Robust Cohen's d for two-sample input |
For more information on the effect sizes, see Algorithms.
Example: Effect="glass"
Data Types: string | char | cell
Known population mean value to compare against, specified as a scalar value. This option is only for single-sample data.
Example: Mean=10
Data Types: single | double
Number of bootstrap replicas to use when computing the bootstrap confidence intervals, specified as a positive integer.
Example: NumBootstraps=1500
Data Types: single | double
Indicator for paired samples, specified as false or
true.
If
Pairedistrue, thenVarianceTypemust be"equal".If
Pairedistrue, thenEffectcannot be"glass".
Example: Paired=true
Data Types: logical
Population variance assumption for two samples, specified as "equal" or
"unequal". If Paired is
"true", then VarianceType must be
"equal".
Example: VarianceType="unequal"
Data Types: string | char
Output Arguments
Effect size information, returned as a table. Effect has a row
for each effect size computed and a column for the value of the effect size, and a
column for the confidence intervals for that effect size, if they are computed.
Data Types: table
Algorithms
Cliff's Delta
Unpaired data
where n1 is the size of the first sample, and n2 is the size of the second sample.
Paired data
meanEffectSizeuses the between-group delta, which compares the differences betweenxandy, but excludes comparisons of paired data. For n paired samples, the result is n(n–1) comparisons [3].
Cohen's d
meanEffectSizecomputes the unbiased estimate of Cohen's d, which is also known as Hedge's g.One-sample
Two-sample
where df is the degrees of freedom, μ is the known population mean to compare against, s is the pooled standard deviation, and J(df) is the bias correction term. The pooled standard deviation is defined as
where n1 is the size of the first sample and n2 is the size of the second sample.
The bias correction term are defined as
where is the gamma function.
Cohen's d follows a noncentral t-distribution and uses it to derive the confidence intervals. So, by default,
meanEffectSizeuses"exact"to compute the confidence intervals for the effect size. See [1] and [4] to see the derivation of the confidence intervals for paired versus unpaired input data.Glass's Delta
where sx is the standard deviation of the control group.
meanEffectSizeuses the data inxas the control group. If you want to use the other sample as the control group, you can swap the data inxandyand swap the sign of the test result.Similar to Cohen's d, Glass's delta also follows a noncentral t-distribution and uses it to derive the confidence intervals. So, by default,
meanEffectSizeuses"exact"to compute the confidence intervals for the effect size [4]. You cannot use this effect size for paired samples.Kolmogorov-Smirnov Test Statistic
This two-sample test statistic is the same as given in Two-Sample Kolmogorov-Smirnov Test.
meanEffectSizeuses bootstrapping to compute the confidence intervals.Mean Difference
One-sample
Two-sample
meanEffectSizecomputes the confidence intervals using the t-distribution with pooled standard deviation in the two-sample case. (In the case of unequal variance assumption for two samples, the confidence intervals are called Welch-Satterthwaite confidence intervals). By default, the function uses"exact"to compute the confidence intervals for the effect size.Median Difference
meanEffectSizecomputes the confidence intervals using bootstrapping for the effect size.Robust Cohen's d
where and are the 20% trimmed means of data in
xandy, respectively. is the pooled 20% Winsorized variance [2].meanEffectSizecomputes the confidence intervals using bootstrapping for the effect size.
References
[1] Cousineau, Denis, and Jean-Christophe Goulet-Pelletier. "A Study of Confidence Intervals for Cohen's d in Within-Subject Designs with New Proposals." The Quantitative Methods for Psychology 17, no. 1 (March 2021): 51--75. https://doi.org/10.20982/tqmp.17.1.p051.
[2] Algina, James, H. J. Keselman, and R. D. Penfield. "An Alternative to Cohen's Standardized Mean Difference Effect Size: A Robust Parameter and Confidence Interval in the Two Independent Groups Case." Psychological Methods 10, no. 3 (Sept 2005): 317–28. https://doi.org/10.1037/1082-989X.10.3.317.
[3] Hess, Melinda, and Jeffrey Kromrey. "Robust Confidence Intervals for Effect Sizes: A Comparative Study of Cohen's d and Cliff's Delta Under Non-normality and Heterogeneous Variances." Annual Meeting of the American Educational Research Association. 2004.
[4] Delacre, Marie, Daniel Lakens, Christophe Ley, Limin Liu, and Christophe Leys. "Why Hedges G's Based on the Non-pooled Standard Deviation Should Be Reported with Welch's T-test." 2021.
[5] Gardner, M. J., and D. G. Altman. Confidence Intervals Rather Than P Values; Estimation Rather Than Hypothesis Testing." BMJ, 292 no. 6522 (March 1986): 746–50. https://doi.org/10.1136/bmj.292.6522.746.
Extended Capabilities
To run in parallel, specify the Options name-value argument in the call to
this function and set the UseParallel field of the
options structure to true using
statset:
Options=statset(UseParallel=true)
For more information about parallel computing, see Run MATLAB Functions with Automatic Parallel Support (Parallel Computing Toolbox).
Version History
Introduced in R2022a
See Also
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)