gardnerAltmanPlot

Gardner-Altman plot for two-sample effect size

Syntax

gardnerAltmanPlot(X,Y)

gardnerAltmanPlot(ax,X,Y)

gardnerAltmanPlot(___,Name=Value)

H = gardnerAltmanPlot(___)

Description

gardnerAltmanPlot(X,Y) generates a Gardner-Altman plot for the mean-difference effect size of data in X and Y.

gardnerAltmanPlot(ax,X,Y) plots into the axes with handle ax.

gardnerAltmanPlot(___,Name=Value) generates a Gardner-Altman plot for options specified using one or more of the Name=Value arguments in combination with any of the previous syntaxes.

H = gardnerAltmanPlot(___) returns a graphics array H for the plot using any of the previous syntaxes.

Examples

Compute Mean Effect Size for Two Independent Samples

Load Fisher's iris data and define the variables for which to compare.

load fisheriris
species2 = categorical(species);
x = meas(species2=='setosa');
y = meas(species2=='virginica');

Compute the median difference effect size of the observations from two independent samples.

effect = meanEffectSize(x,y,Effect="mediandiff")

effect=1×2 table
                        Effect    ConfidenceIntervals
                        ______    ___________________

    MedianDifference     -1.5     -1.8259       -1.3 

meanEffectSize by default assumes independent samples (that is, Paired=false). The function uses bootstrapping to estimate the confidence intervals when effect type is median difference.

Visualize the median difference effect size using Gardner-Altman plot.

gardnerAltmanPlot(x,y,Effect="mediandiff");

Gardner-Altman plot displays the two sample data on the left. The median of the sample Y corresponds to the zero effect size on the effect size axis, which is the yellow axis line on the right. The median of the sample X corresponds to the value of the effect size on the effect size axis. The plot displays the actual median difference effect size value and the confidence intervals with the vertical error bar.

Specify Bootstrap Options

Load Fisher's iris data and define the variables for which to compare.

load fisheriris
species2 = categorical(species);
x = meas(species2=='setosa');
y = meas(species2=='virginica');

Compute the Cohen's d effect size for the observations from two independent samples and compute the 95% confidence intervals for the effect size. meanEffectSize by default uses the exact formula based on the noncentral t-distribution to estimate the confidence intervals when the effect type is Cohen's d. Specify the bootstrapping options:

• Tell meanEffectSize to use bootstrapping for confidence interval computation.

• Use parallel computing for bootstrapping computations. You need Parallel Computing Toolbox™ for this option.

• Use 3000 bootstrap replicas.

rng(123) % For reproducibility
effect = meanEffectSize(x,y,Effect="cohen",ConfidenceIntervalType="bootstrap", ...
      BootstrapOptions=statset(UseParallel=true),NumBootstraps=3000)

Starting parallel pool (parpool) using the 'local' profile ...
Connected to the parallel pool (number of workers: 6).

effect=1×2 table
               Effect     ConfidenceIntervals
               _______    ___________________

    CohensD    -3.0536    -3.5611    -2.3219 

Use the same options in Gardner-Altman plot to visualize the effect size.

gardnerAltmanPlot(x,y,Effect="cohen",ConfidenceIntervalType="bootstrap", ...
      BootstrapOptions=statset(UseParallel=true),NumBootstraps=3000);

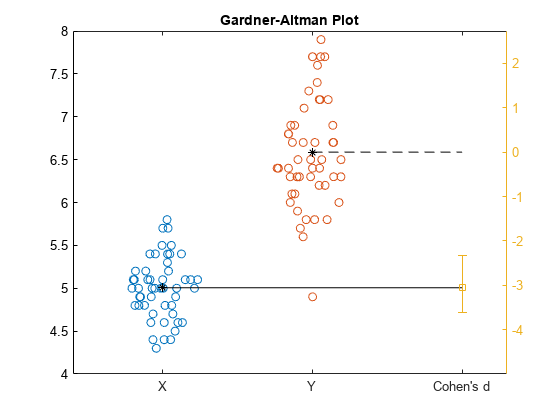
Gardner-Altman plot displays the two sample data on the left. The mean of the sample Y corresponds to the zero effect size on the effect size axis, which is the yellow axis line on the right. The mean of the sample X corresponds to the value of the effect size on the effect size axis. The plot displays the Cohen's d effect size value and the confidence intervals with the vertical error bar.

Compare Paired Sample Means

Load exam grades data and define the variables for which to compare.

load examgrades
x = grades(:,1);
y = grades(:,2);

Compute the mean difference effect size of the grades from the paired samples and 95% confidence intervals for the effect size.

effect = meanEffectSize(x,y,Paired=true)

effect=1×2 table
                       Effect     ConfidenceIntervals
                      ________    ___________________

    MeanDifference    0.016667    -1.3311     1.3644 

meanEffectSize uses the exact method to estimate the confidence intervals when you use mean difference effect size.

You can use a different effect size type (note that you can't use Glass's delta for paired samples). Use robust Cohen's d to compare the paired-sample means. Compute the 97% confidence intervals for the effect size.

effect = meanEffectSize(x,y,Paired=true,Effect="robustcohen",Alpha=0.03)

effect=1×2 table
                      Effect     ConfidenceIntervals
                     ________    ___________________

    RobustCohensD    0.059128    -0.1405    0.26573 

meanEffectSize uses bootstrapping to estimate the confidence intervals when you use robust Cohen's d as the effect size.

Visualize the effect size using Gardner-Altman plot. Again use robust Cohen's d as the effect size and compute the 97% confidence intervals.

gardnerAltmanPlot(x,y,Paired=true,Effect="robustcohen",Alpha=0.03);

Gardner-Altman plot displays the paired data on the left. Blue lines show the values that are increasing and the red lines show the values that are decreasing from the first sample to the corresponding values in the paired sample, respectively. On the right side of the plot, you see the robust Cohen's d effect size with the 97% confidence intervals.

Input Arguments

X — Input data

numeric vector

Input data, specified as a numeric vector.

Data Types: single | double

Y — Input data

numeric vector

Input data, specified as a numeric vector.

Data Types: single | double

ax — Axes for plot

Axes object | UIAxes object

Axes for the plot, specified as an Axes or UIAxes object. If you do not specify ax, then gardnerAltmanPlot creates the plot using the current axes. For more information on creating an axes object, see axes and uiaxes.

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Example: Effect="cliff",Alpha=0.03,ConfidenceIntervalType="bootstrap",VarianceType=unequal specifies to use the Cliff's Delta effect size and compute the 97% confidence intervals using bootstrapping and assume the samples come from populations with unequal variances..

Alpha — Confidence level

0.05 (default) | value from 0 to 1

Confidence level, specified as a numeric value from 0 to 1. Default value of Alpha, 0.05, corresponds to 95% confidence level.

Example: Alpha=0.025

Data Types: single | double

BootstrapOptions — Options for bootstrap confidence interval computation in parallel

structure

Options for bootstrap confidence interval computation in parallel, specified as a structure generated by using statset('bootci'). gardnerAltmanPlot uses the following fields:

Field	Description
'Streams'	A RandStream object or cell array of such objects. If you do not specify Streams, gardnerAltmanPlot uses the default stream or streams. If you specify Streams, use a single object except when all of the following conditions exist: You have an open parallel pool. UseParallel is true. UseSubstreams is false. In this case, use a cell array the same size as the parallel pool. If a parallel pool is not open, then Streams must supply a single random number stream.
'UseParallel'	The default is false, indicating serial computation.
'UseSubstreams'	Set to true to compute in parallel in a reproducible fashion. The default is false. To compute reproducibly, set Streams to a type allowing substreams: 'mlfg6331_64' or 'mrg32k3a'.

Computing bootstrap confidence intervals in parallel requires Parallel Computing Toolbox™.

Example: BootstrapOptions=options

Data Types: struct

ConfidenceIntervalType — Type of confidence interval

"exact" | "bootstrap" | "none"

Type of confidence interval to compute, specified as "exact", "bootstrap", or "none". The default is "exact" when there is an exact formula for the effect size or "bootstrap" otherwise. "none" is for not computing any confidence intervals.

Default is "exact" for Cliff's Delta, Glass's delta, mean difference, and Cohen's d and "bootstrap" for Kolmogorov-Smirnov statistic, median difference, and Robust Cohen's d. If you specify confidence interval type as "exact" for Kolmogorov-Smirnov statistic, median difference, and Robust Cohen's d, gardnerAltmanPlot returns an error.

Example: ConfidenceIntervalType="none"

Data Types: string | char

Effect — Effect size to compute

"meandiff" (default) | "cohen" | "cliff" | "glass" | "kstest" | "mediandiff" | "robustcohen"

Effect size to compute, specified as one of the following:

Effect size option	Definition
"cohen"	Cohen's d for two-sample input.
"cliff"	Cliff's Delta.
"glass"	Glass's delta. gardnerAltmanPlot doesn't support this option for paired data.
"kstest"	Kolmogorov-Smirnov statistic.
"mediandiff"	Median difference.
"meandiff"	Mean difference.
"robustcohen"	Robust Cohen's d for two-sample input.

Example: Effect="glass"

Data Types: string | char

NumBootstraps — Number of bootstrap replicas

1000 (default) | positive integer

Number of bootstrap replicas to use when computing the bootstrap confidence intervals, specified as a positive integer.

Example: NumBootstraps=1500

Data Types: single | double

Paired — Indicator for paired samples

false (default) | true

Indicator for paired samples, specified as a logical value.

• If Paired is "true", then VarianceType must be "equal".

• If Paired is "true", then Effect cannot be "glass".

Example: Paired="true"

Data Types: logical

VarianceType — Population variance assumption for two samples

"equal" (default) | "unequal"

Population variance assumption for two samples, specified as either "equal" or "unequal". If Paired is "true", then VarianceType must be "equal".

Example: VarianceType="unequal"

Data Types: string | char

Output Arguments

H — Graphics array for the plot

1-by-5 graphics array (default) | 1-by-4 graphics array

Graphics array for the plot, specified as a 1-by-5 or a 1-by-4 graphics array depending on the effect size you choose and whether the data is unpaired or paired as follows.

• Unpaired data (Paired="false"):

  • "meandiff", "glass", "cohen" or "robustcohen" effect size:

    H is a 1-by-5 graphics array that holds two Scatter objects, one ErrorBar object, and two Line objects.

    The Scatter objects represent the scatter plots of the input data in X and Y, the ErrorBar object represents the effect size and its confidence intervals, and the Line objects represent the mean line from the control sample to the effect size and the other sample to 0.

  • "mediandiff" effect size:

    H is a 1-by-5 graphics array that holds two Scatter objects, one ErrorBar object, and two Line objects that represent the median lines from the two sample data sets.

  • "cliff" or "kstest" effect size:

    H is a 1-by-4 graphics array that holds two Scatter objects, one ErrorBar object, and one Line object that represents the line at 0 to indicate no effect between the two groups.

• Paired data (Paired="true"):

  • H holds 1-3 Line objects, representing the lines for the pairs that increased, decreased, or stayed the same and one ErrorBar object, representing the effect size and its confidence intervals.

For all cases, if you choose not to generate any confidence intervals for the effect (ConfidenceIntervalType="none"), the ErrorBar object will instead be a Line object.

Use H to inspect and adjust the properties of the objects. To learn more about the object properties, see Scatter Properties, ErrorBar Properties, and Line Properties, respectively.

Algorithms

Effect Sizes

• Cliff's Delta

  • Unpaired data

    $$\delta =\frac{{\displaystyle \sum _{i,j=1}^{n_1,n_2}\left(x_i>y_j\right)-\left(x_i<y_j\right)}}{n_1*n_2},$$

    where n₁ is the size of the first sample and n₂ is the size of the second sample.

  • Paired data

    gardnerAltmanPlot uses the between-group delta, which is comparing the differences from x and y, but excluding comparisons of paired data. For n paired samples, this results in n(n-1) comparisons [3].

• Cohen's d

  gardnerAltmanPlot computes the unbiased estimate of Cohen's d, which is also known as Hedge's g.

  • One-sample

    $$d=J\left(df\right)*\frac{\left(\overline{x}-\mu \right)}{s}$$

  • Two-sample

    $$d=J\left(df\right)*\frac{\left(\overline{x}-\overline{y}\right)}{s}$$

  where df is the degrees of freedom, μ is the known population mean to compare against, s is the pooled standard deviation, and J(df) is the bias correction term. The pooled standard deviation and the bias correction term are defined as follows, respectively.

  $$s=\sqrt{\frac{\left(n_1-1\right)s_1^2+\left(n_2-1\right)s_2^2}{n_1+n_2-2}},$$

  where n₁ is the size of the first sample and n₂ is the size of the second sample.

  $$J\left(df\right)=\frac{\Gamma \left(df/2\right)}{\sqrt{df/2}\Gamma \left(\left(df-1\right)/2\right)},$$

  where $$\Gamma \left(\right)$$ is the gamma function.

  Cohen's d follows a noncentral t-distribution, and uses that to derive the confidence intervals. Hence, gardnerAltmanPlot by default uses "exact" to compute the confidence intervals for the effect size. See [1] and [4] to see the derivation of the confidence intervals for paired versus unpaired input data.

• Glass's Delta

  $$D=\frac{\overline{x}-\overline{y}}{s_x},$$

  where s_x is the standard deviation of the control group. gardnerAltmanPlot uses the data in x as the control group. If you wish to use the other sample as the control group, you can swap the data in x and y and swap the sign of the test result.

  Similar to Cohen's d, Glass's delta also follows a noncentral t-distribution, and uses that to derive the confidence intervals. Hence, gardnerAltmanPlot by default uses "exact" to compute the confidence intervals for the effect size [4]. You can't use this effect size for paired samples.

• Kolmogorov-Smirnov Test Statistic

  This two-sample test statistic is the same as given in Two-Sample Kolmogorov-Smirnov Test. gardnerAltmanPlot uses bootstrapping to compute the confidence intervals.

• Mean Difference

  • One-sample

    $$m=\left(\overline{x}-\mu \right)$$

  • Two-sample

    $$m=\left(\overline{x}-\overline{y}\right)$$

  gardnerAltmanPlot computes the confidence intervals using the t-distribution (using pooled standard deviation in the two-sample case. In case of unequal variance assumption for two samples, the confidence intervals are called Welch-Satterthwaite confidence intervals). The function by default uses the "exact" method to compute the confidence intervals.

• Median Difference

  $$M\text{ = }median\left(x\right)-median\left(y\right)$$

  gardnerAltmanPlot computes the confidence intervals using bootstrapping for this effect size.

• Robust Cohen's d

  $$d=0.643*J\left(df\right)*\frac{\left({\overline{x}}_t-{\overline{y}}_t\right)}{s_w},$$

  where $${\overline{x}}_t$$ and $${\overline{y}}_t$$ are the 20% trimmed mean of data in x and y, respectively. $${\text{s}}_w$$ is the pooled 20% Winsorized variance [2].

  gardnerAltmanPlot computes the confidence intervals using bootstrapping for this effect size.

References

[1] Cousineau, Denis and Jean-Christophe Goulet-Pelletier. "A study of confidence intervals for Cohen's d in within-subject designs with new proposals". The Quantitative Methods for Psychology, 2021.

[2] Algina, James, H. J. Keselman, and R. D. Penfield. "An Alternative to Cohen's Standardized Mean Difference Effect Size: A Robust Parameter and Confidence Interval in the Two Independent Groups Case". Psychological Methods, Vol. 10, No. 3, pp. 317–328. 2005.

[3] Hess, Melinda and Jeffrey Kromrey. "Robust Confidence Intervals for Effect Sizes: A Comparative Study of Cohen's d and Cliff's Delta Under Non-normality and Heterogeneous Variances". Annual Meeting of the American Educational Research Association. 2004.

[4] Delacre, Marie, Daniel Lakens, Christophe Ley, Limin Liu, and Christophe Leys. "Why Hedges G's Based on the Non-pooled Standard Deviation Should Be Reported with Welch's T-test". 2021.

[5] Gardner, M. J. and D. G. Altman. "Confidence intervals rather than P values: estimation rather than hypothesis testing". BMJ, Vol. 292 No. 6522, pp. 746–750. 1986.

Extended Capabilities

Automatic Parallel Support

Accelerate code by automatically running computation in parallel using Parallel Computing Toolbox™.

To run in parallel, specify the 'Options' name-value argument in the call to this function and set the 'UseParallel' field of the options structure to true using statset.

For example: 'Options',statset('UseParallel',true)

For more information about parallel computing, see Run MATLAB Functions with Automatic Parallel Support (Parallel Computing Toolbox).

Version History

Introduced in R2022a