predict
Predict responses for new observations from incremental drift-aware learning model
Since R2022b
Syntax
Description
[
also returns the classification scores, posterior probabilities, or the negated average
binary losses in yfit,m] = predict(___)m when Mdl.BaseLearner is an
incremental learning model for classification, using any of the input argument combinations
in the previous syntaxes. What m contains depends on the type of the
Mdl.BaseLearner model object.
Examples
Create the random concept data and the concept drift generator using the helper functions HelperRegrGenerator and HelperConceptDriftGenerator, respectively.
concept1 = HelperRegrGenerator(NumFeatures=100,NonZeroFeatures=[1,20,40,50,55], ... FeatureCoefficients=[4,5,10,-2,-6],NoiseStd=1.1,TableOutput=false); concept2 = HelperRegrGenerator(NumFeatures=100,NonZeroFeatures=[10,20,45,56,80], ... FeatureCoefficients=[4,5,10,-2,-6],NoiseStd=1.1,TableOutput=false); driftGenerator = HelperConceptDriftGenerator(concept1,concept2,15000,1000);
HelperRegrGenerator generates streaming data using features and feature coefficients for regression specified in the call to the function. At each step, the function samples the predictors from a normal distribution. Then, the function computes the response using the feature coefficients and predictor values and adding a random noise from a normal distribution with mean zero and specified noise standard deviation. The software returns the data in matrices for using in incremental learners.
HelperConceptDriftGenerator establishes the concept drift. The object uses a sigmoid function 1./(1+exp(-4*(numobservations-position)./width)) to decide the probability of choosing the first stream when generating data [3]. In this case, the position argument is 15000 and the width argument is 1000. As the number of observations exceeds the position value minus half of the width, the probability of sampling from the first stream when generating data decreases. The sigmoid function allows a smooth transition from one stream to the other. Larger width values indicate a larger transition period where both streams are approximately equally likely to be selected.
Initiate an incremental drift-aware model for regression as follows:
Create an incremental linear model for regression. Specify the linear regression model type and solver type.
Initiate an incremental concept drift detector that uses the Hoeffding's Bounds Drift Detection Method with moving average (HDDMA).
Using the incremental linear model and the concept drift detector, instantiate an incremental drift-aware model. Specify the training period as 6000 observations.
baseMdl = incrementalRegressionLinear(Learner="leastsquares",Solver="sgd",EstimationPeriod=1000,Standardize=false); dd = incrementalConceptDriftDetector("hddma",Alternative="greater",InputType="continuous",WarmupPeriod=1000); idaMdl = incrementalDriftAwareLearner(baseMdl,DriftDetector=dd,TrainingPeriod=6000);
Preallocate the number of variables in each chunk and the number of iterations for creating a stream of data.
numObsPerChunk = 10; numIterations = 4000;
Preallocate the variables for tracking the drift status and drift time, and storing the regression error.
dstatus = zeros(numIterations,1); statusname = strings(numIterations,1); driftTimes = []; ce = array2table(zeros(numIterations,2),VariableNames=["Cumulative" "Window"]);
Simulate a data stream with incoming chunks of 10 observations each and perform incremental drift-aware learning. At each iteration:
Simulate predictor data and labels, and update the drift generator using the helper function
hgenerate.Call
updateMetricsto update the performance metrics andfitto fit the incremental drift-aware model to the incoming data.Track and record the drift status and the regression error for visualization purposes.
rng(12); % For reproducibility for j = 1:numIterations % Generate data [driftGenerator,X,Y] = hgenerate(driftGenerator,numObsPerChunk); % Update performance metrics and fit idaMdl = updateMetrics(idaMdl,X,Y); idaMdl = fit(idaMdl,X,Y); % Record drift status and regression error statusname(j) = string(idaMdl.DriftStatus); ce{j,:} = idaMdl.Metrics{"MeanSquaredError",:}; if idaMdl.DriftDetected dstatus(j) = 2; driftTimes(end+1) = j; elseif idaMdl.WarningDetected dstatus(j) = 1; else dstatus(j) = 0; end end
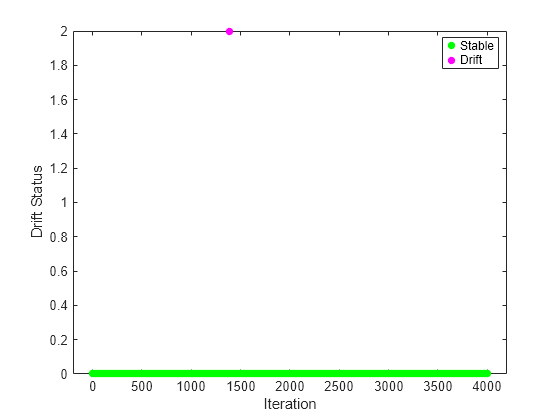
Plot the drift status versus the iteration number.
figure() gscatter(1:numIterations,dstatus,statusname,'gmr','o',5,'on',"Iteration","Drift Status","filled")
Plot the cumulative and per window regression error. Mark the warmup and training periods, and where the drift was introduced.
figure() h = plot(ce.Variables); xlim([0 numIterations]) ylim([0 20]) ylabel("Mean Squared Error") xlabel("Iteration") xline((idaMdl.MetricsWarmupPeriod+idaMdl.BaseLearner.EstimationPeriod)/numObsPerChunk,"g-.","Estimation Period + Warmup Period",LineWidth=1.5) xline((idaMdl.MetricsWarmupPeriod+idaMdl.BaseLearner.EstimationPeriod)/numObsPerChunk+driftTimes,"g-.","Estimation Period + Warmup Period",LineWidth=1.5) xline(idaMdl.TrainingPeriod/numObsPerChunk,"b-.","Training Period",LabelVerticalAlignment="middle",LineWidth=1.5) xline(driftTimes,"m--","Drift",LabelVerticalAlignment="middle",LineWidth=1.5) legend(h,ce.Properties.VariableNames) legend(h,Location="best")

After the detection of drift, the fit function calls the reset function to reset the incremental drift-aware learner, hence the base learner and the drift detector. The updateMetrics function waits for idaMdl.BaseLearner.EstimationPeriod+idaMdl.MetricsWarmupPeriod observations to start updating model performance metrics again.
Generate new data. Reorient the predictor variables in columns.
[driftGenerator,X,Y] = hgenerate(driftGenerator,500); X = X';
Predict responses on new data. Specify the orientation of the predictor variables.
yhat = predict(idaMdl,X,ObservationsIn="columns");Compute and plot the residuals.
res = Y - yhat; plot(res) ylabel("Residuals") xlabel("New data points")

The residuals appear symmetrically spread around 0 for new data.
Create the random concept data using the HelperSineGenerator and concept drift generator HelperConceptDriftGenerator.
concept1 = HelperSineGenerator("ClassificationFunction",1,"IrrelevantFeatures",true,"TableOutput",false); concept2 = HelperSineGenerator("ClassificationFunction",3,"IrrelevantFeatures",true,"TableOutput",false); driftGenerator = HelperConceptDriftGenerator(concept1,concept2,15000,1000);
When ClassificationFunction is 1, HelperSineGenerator labels all points that satisfy x1 < sin(x2) as 1, otherwise the function labels them as 0. When ClassificationFunction is 3, this is reversed. That is, HelperSineGenerator labels all points that satisfy x1 >= sin(x2) as 1, otherwise the function labels them as 0.
HelperConceptDriftGenerator establishes the concept drift. The object uses a sigmoid function 1./(1+exp(-4*(numobservations-position)./width)) to decide the probability of choosing the first stream when generating data [1]. In this case, the position argument is 15000 and the width argument is 1000. As the number of observations exceeds the position value minus half of the width, the probability of sampling from the first stream when generating data decreases. The sigmoid function allows a smooth transition from one stream to the other. Larger width values indicate a larger transition period where both streams are approximately equally likely to be selected.
Instantiate an incremental drift-aware model as follows:
Create an incremental Naive Bayes classification model for binary classification.
Initiate an incremental concept drift detector that uses the Hoeffding's Bounds Drift Detection Method with moving average (HDDMA).
Using the incremental linear model and the concept drift detector, instantiate an incremental drift-aware model. Specify the training period as 5000 observations.
BaseLearner = incrementalClassificationLinear(Solver="sgd"); dd = incrementalConceptDriftDetector("hddma"); idaMdl = incrementalDriftAwareLearner(BaseLearner,DriftDetector=dd,TrainingPeriod=5000);
Preallocate the number of variables in each chunk and number of iterations for creating a stream of data.
numObsPerChunk = 10; numIterations = 4000;
Preallocate the variables for tracking the drift status and drift time, and storing the classification error.
dstatus = zeros(numIterations,1); statusname = strings(numIterations,1); ce = array2table(zeros(numIterations,2),VariableNames=["Cumulative" "Window"]); driftTimes = [];
Simulate a data stream with incoming chunks of 10 observations each and perform incremental drift-aware learning. At each iteration:
Simulate predictor data and labels, and update the drift generator using the helper function
hgenerate.Call
updateMetricsAndFitto update the performance metrics and fit the incremental drift-aware model to the incoming data.Track and record the drift status and the classification error for visualization purposes.
rng(12); % For reproducibility for j = 1:numIterations % Generate data [driftGenerator,X,Y] = hgenerate(driftGenerator,numObsPerChunk); % Update performance metrics and fit idaMdl = updateMetricsAndFit(idaMdl,X,Y); % Record drift status and classification error statusname(j) = string(idaMdl.DriftStatus); ce{j,:} = idaMdl.Metrics{"ClassificationError",:}; if idaMdl.DriftDetected dstatus(j) = 2; driftTimes(end+1) = j; elseif idaMdl.WarningDetected dstatus(j) = 1; else dstatus(j) = 0; end end
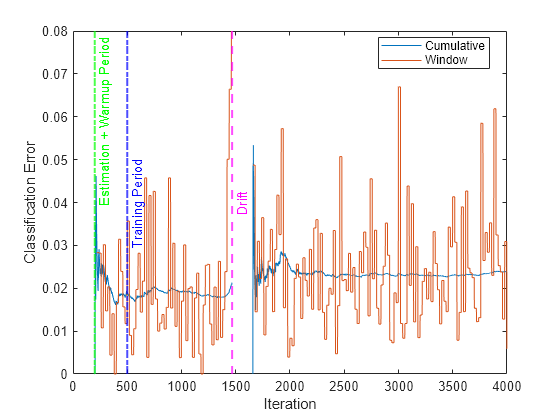
Plot the cumulative and per window classification error. Mark the warmup and training periods, and where the drift was introduced.
h = plot(ce.Variables); xlim([0 numIterations]) ylim([0 0.08]) ylabel("Classification Error") xlabel("Iteration") xline((idaMdl.BaseLearner.EstimationPeriod+idaMdl.MetricsWarmupPeriod)/numObsPerChunk,"g-.","Estimation + Warmup Period",LineWidth=1.5) xline(idaMdl.TrainingPeriod/numObsPerChunk,"b-.","Training Period",LabelVerticalAlignment="middle",LineWidth=1.5) xline(driftTimes,"m--","Drift",LabelVerticalAlignment="middle",LineWidth=1.5) legend(h,ce.Properties.VariableNames) legend(h,Location="best")
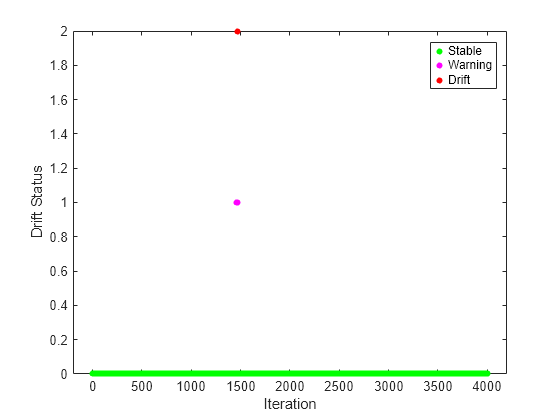
Plot the drift status versus the iteration number.
gscatter(1:numIterations,dstatus,statusname,'gmr','o',4,'on',"Iteration","Drift Status","Filled")
Generate new data of 500 observations. Predict class labels and classification scores for new data.
numnewdata = 500; [driftGenerator,X,Y] = hgenerate(driftGenerator,numnewdata); [yhat,cscores] = predict(idaMdl,X);
Compute ROC and plot the results.
roc = rocmetrics(Y,cscores,idaMdl.BaseLearner.ClassNames); plot(roc)

For each class, the plot function plots a ROC curve and displays a filled circle marker at the model operating point. The legend displays the class name and AUC value for each curve. In a binary classification problem, the two ROC curves are symmetric, and the AUC values are identical.
Compute the accuracy of the model.
accuracy = sum(Y==yhat)/500
accuracy = 0.9780
The model predicts the new class labels with high accuracy.
Input Arguments
Incremental drift-aware learning model fit to streaming data, specified as an incrementalDriftAwareLearner model object. You can create
Mdl using the incrementalDriftAwareLearner
function. For more details, see the object reference page.
Chunk of predictor data for which to predict responses or labels, specified as a
floating-point matrix of n observations and
Mdl.BaseLearner.NumPredictors predictor variables.
When Mdl.BaseLearner accepts the
ObservationsIn name-value argument, the value of
ObservationsIn determines the orientation of the variables and
observations. The default ObservationsIn value is
"rows", which indicates that observations in the predictor data are
oriented along the rows of X.
Note
predict supports only floating-point
input predictor data. If your input data includes categorical data, you must prepare an encoded
version of the categorical data. Use dummyvar to convert each categorical variable
to a numeric matrix of dummy variables. Then, concatenate all dummy variable matrices and any
other numeric predictors. For more details, see Dummy Variables.
Data Types: single | double
Predictor data observation dimension, specified as "columns" or
"rows".
predict supports
ObservationsIn=dimension only if
Mdl.BaseLearner supports the ObservationsIn
name-value argument.
Data Types: char | string
Output Arguments
Predicted responses (labels), returned as a floating-point vector, categorical or
character array, string or logical vector, or cell array of character vectors with
n rows. n is the number of observations in
X, and yfit( is
the predicted response (label) for observation
j)j
For classification problems,
yfithas the same data type as the class names stored inMdl.BaseLearner.ClassNames. The software treats string arrays as cell arrays of character vectors.For regression problems,
yfitis a floating-point vector.
Classification scores, posterior probabilities, or negated average binary losses,
returned as a floating-point matrix when Mdl.BaseLearner is an
incremental classification model.
When
Mdl.BaseLearneris anincrementalClassificationLinearorincrementalClassificationKernelmodel object,mcontains the raw classification scores or posterior probabilities depending on the learner type. For more information, seepredict(incrementalClassificationLinear) orpredict(incrementalClassificationKernel).
When
Mdl.BaseLearneris anincrementalClassificationNaiveBayesmodel object,mcontains the posterior probabilities. For more information, seepredict(incrementalClassificationNaiveBayes).
When
Mdl.BaseLearneris anincrementalClassificationECOCmodel object,mcontains the negated average binary losses. For more information, seepredict(incrementalClassificationECOC).
Expected misclassification costs, returned as an
n-by-numel(Mdl.BaseLearner.ClassNames)
floating-point matrix when Mdl.BaseLearner is an
incrementalClassificationNaiveBayes model. For more information, see
predict
(incrementalClassificationNaiveBayes).
References
[1] Barros, Roberto S.M. , et al. "RDDM: Reactive drift detection method." Expert Systems with Applications. vol. 90, Dec. 2017, pp. 344-55. https://doi.org/10.1016/j.eswa.2017.08.023.
[2] Bifet, Albert, et al. "New Ensemble Methods for Evolving Data Streams." Proceedings of the 15th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. ACM Press, 2009, p. 139. https://doi.org/10.1145/1557019.1557041.
[3] Gama, João, et al. "Learning with drift detection". Advances in Artificial Intelligence – SBIA 2004, edited by Ana L. C. Bazzan and Sofiane Labidi, vol. 3171, Springer Berlin Heidelberg, 2004, pp. 286–95. https://doi.org/10.1007/978-3-540-28645-5_29.
Version History
Introduced in R2022b
See Also
fit | incrementalDriftAwareLearner | loss | updateMetrics | updateMetricsAndFit
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)