incrementalLearner
Convert multiclass error-correcting output codes (ECOC) model to incremental learner
Since R2022a
Description
IncrementalMdl = incrementalLearner(Mdl)IncrementalMdl, using the hyperparameters and parameters of the
traditionally trained ECOC model for multiclass classification, Mdl.
Because its property values reflect the knowledge gained from Mdl,
IncrementalMdl can predict labels given new observations, and it is
warm, meaning that its predictive performance is tracked.
IncrementalMdl = incrementalLearner(Mdl,Name=Value)IncrementalMdl before its
predictive performance is tracked. For example,
MetricsWarmupPeriod=50,MetricsWindowSize=100 specifies a preliminary
incremental training period of 50 observations before performance metrics are tracked, and
specifies processing 100 observations before updating the window performance metrics.
Examples
Train a multiclass ECOC classification model by using fitcecoc, and then convert it to an incremental learner.
Load Data
Load the human activity data set.
load humanactivityFor details on the data set, enter Description at the command line.
Train ECOC Model
Fit a multiclass ECOC classification model to the entire data set.
Mdl = fitcecoc(feat,actid);
Mdl is a ClassificationECOC model object representing a traditionally trained ECOC classification model.
Convert Trained Model
Convert the traditionally trained ECOC classification model to a model for incremental learning.
IncrementalMdl = incrementalLearner(Mdl)
IncrementalMdl =
incrementalClassificationECOC
IsWarm: 1
Metrics: [1×2 table]
ClassNames: [1 2 3 4 5]
ScoreTransform: 'none'
BinaryLearners: {10×1 cell}
CodingName: 'onevsone'
Decoding: 'lossweighted'
Properties, Methods
IncrementalMdl is an incrementalClassificationECOC model object prepared for incremental learning.
The
incrementalLearnerfunction initializes the incremental learner by passing the coding design and model parameters for binary learners to it, along with other informationMdlextracts from the training data.IncrementalMdlis warm (IsWarmis1), which means that incremental learning functions can track performance metrics and make predictions.
Predict Responses
An incremental learner created from converting a traditionally trained model can generate predictions without further processing.
Predict classification scores for all observations using both models.
[~,ttscores] = predict(Mdl,feat); [~,ilcores] = predict(IncrementalMdl,feat); compareScores = norm(ttscores - ilcores)
compareScores = 0
The difference between the scores generated by the models is 0.
Use a trained ECOC model to initialize an incremental learner. Prepare the incremental learner by specifying a metrics warm-up period and a metrics window size.
Load the human activity data set.
load humanactivityFor details on the data set, enter Description at the command line
Randomly split the data in half: the first half for training a model traditionally, and the second half for incremental learning.
n = numel(actid); rng(1) % For reproducibility cvp = cvpartition(n,Holdout=0.5); idxtt = training(cvp); idxil = test(cvp); % First half of data Xtt = feat(idxtt,:); Ytt = actid(idxtt); % Second half of data Xil = feat(idxil,:); Yil = actid(idxil);
Fit an ECOC model to the first half of the data.
Mdl = fitcecoc(Xtt,Ytt);
Convert the traditionally trained ECOC model to a model for incremental learning. Specify the following:
A performance metrics warm-up period of 2000 observations
A metrics window size of 500 observations
IncrementalMdl = incrementalLearner(Mdl, ...
MetricsWarmupPeriod=2000,MetricsWindowSize=500);By default, incrementalClassificationECOC uses classification error loss to measure the performance of the model.
Fit the incremental model to the second half of the data by using the updateMetricsAndFit function. At each iteration:
Simulate a data stream by processing 20 observations at a time.
Overwrite the previous incremental model with a new one fitted to the incoming observations.
Store the first model coefficient of the first binary learner , the cumulative metrics, and the window metrics to see how they evolve during incremental learning.
% Preallocation nil = numel(Yil); numObsPerChunk = 20; nchunk = ceil(nil/numObsPerChunk); ce = array2table(zeros(nchunk,2),VariableNames=["Cumulative","Window"]); beta11 = [IncrementalMdl.BinaryLearners{1}.Beta(1); zeros(nchunk+1,1)]; % Incremental fitting for j = 1:nchunk ibegin = min(nil,numObsPerChunk*(j-1) + 1); iend = min(nil,numObsPerChunk*j); idx = ibegin:iend; IncrementalMdl = updateMetricsAndFit(IncrementalMdl,Xil(idx,:),Yil(idx)); ce{j,:} = IncrementalMdl.Metrics{"ClassificationError",:}; beta11(j+1) = IncrementalMdl.BinaryLearners{1}.Beta(1); end
IncrementalMdl is an incrementalClassificationECOC model object trained on all the data in the stream. During incremental learning and after the model is warmed up, updateMetricsAndFit checks the performance of the model on the incoming observations, and then fits the model to those observations.
To see how the performance metrics and evolve during training, plot them on separate tiles.
t = tiledlayout(2,1); nexttile plot(beta11) ylabel("\beta_{11}") xlim([0 nchunk]); xline(IncrementalMdl.MetricsWarmupPeriod/numObsPerChunk,"r-."); nexttile plot(ce.Variables); xlim([0 nchunk]); ylabel("Classification Error") xline(IncrementalMdl.MetricsWarmupPeriod/numObsPerChunk,"r-."); legend(ce.Properties.VariableNames,Location="best") xlabel(t,"Iteration")
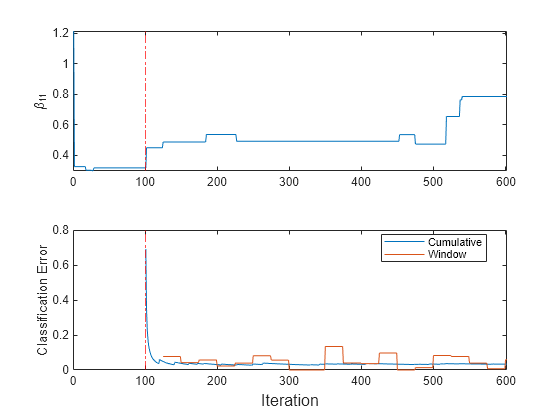
The plots indicate that updateMetricsAndFit performs the following actions:
Fit during all incremental learning iterations.
Compute the performance metrics after the metrics warm-up period (red vertical line) only.
Compute the cumulative metrics during each iteration.
Compute the window metrics after processing 500 observations (25 iterations).
Input Arguments
Traditionally trained ECOC model for multiclass classification, specified as a
ClassificationECOC or CompactClassificationECOC model object returned by fitcecoc or compact, respectively.
Note
When you train
Mdl, you must specify theLearnersname-value argument offitcecocto use support vector machine (SVM) binary learner templates (templateSVM) or linear classification model binary learner templates (templateLinear).Incremental learning functions support only numeric input predictor data. If
Mdlwas trained on categorical data, you must prepare an encoded version of the categorical data to use incremental learning functions. Usedummyvarto convert each categorical variable to a numeric matrix of dummy variables. Then, concatenate all dummy variable matrices and any other numeric predictors, in the same way that the training function encodes categorical data. For more details, see Dummy Variables.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: Decoding="lossbased",MetricsWindowSize=100 specifies to use
the loss-based decoding scheme and to process 100 observations before updating the window
performance metrics.
ECOC Classifier Options
Binary learner loss function, specified as a built-in loss function name or function handle.
This table describes the built-in functions, where yj is the class label for a particular binary learner (in the set {–1,1,0}), sj is the score for observation j, and g(yj,sj) is the binary loss formula.
Value Description Score Domain g(yj,sj) "binodeviance"Binomial deviance (–∞,∞) log[1 + exp(–2yjsj)]/[2log(2)] "exponential"Exponential (–∞,∞) exp(–yjsj)/2 "hamming"Hamming [0,1] or (–∞,∞) [1 – sign(yjsj)]/2 "hinge"Hinge (–∞,∞) max(0,1 – yjsj)/2 "linear"Linear (–∞,∞) (1 – yjsj)/2 "logit"Logistic (–∞,∞) log[1 + exp(–yjsj)]/[2log(2)] "quadratic"Quadratic [0,1] [1 – yj(2sj – 1)]2/2 The software normalizes binary losses so that the loss is 0.5 when yj = 0. Also, the software calculates the mean binary loss for each class [1].
For a custom binary loss function, for example
customFunction, specify its function handleBinaryLoss=@customFunction.customFunctionhas this form:bLoss = customFunction(M,s)
Mis the K-by-B coding matrix stored inMdl.CodingMatrix.sis the 1-by-B row vector of classification scores.bLossis the classification loss. This scalar aggregates the binary losses for every learner in a particular class. For example, you can use the mean binary loss to aggregate the loss over the learners for each class.K is the number of classes.
B is the number of binary learners.
For an example of a custom binary loss function, see Predict Test-Sample Labels of ECOC Model Using Custom Binary Loss Function. This example is for a traditionally trained model. You can define a custom loss function for incremental learning as shown in the example.
For more information, see Binary Loss.
Data Types: char | string | function_handle
Decoding scheme, specified as "lossweighted" or
"lossbased".
The decoding scheme of an ECOC model specifies how the software aggregates the binary losses and determines the predicted class for each observation. The software supports two decoding schemes:
"lossweighted"— The predicted class of an observation corresponds to the class that produces the minimum sum of the binary losses over binary learners."lossbased"— The predicted class of an observation corresponds to the class that produces the minimum average of the binary losses over binary learners.
For more information, see Binary Loss.
Example: Decoding="lossbased"
Data Types: char | string
Performance Metrics Options
Model performance metrics to track during incremental learning with the updateMetrics or updateMetricsAndFit function, specified as
"classiferror" (classification error, or
misclassification error rate), a function handle (for example,
@metricName), a structure array of function handles, or a cell
vector of names, function handles, or structure arrays.
To specify a custom function that returns a performance metric, use function handle notation. The function must have this form.
metric = customMetric(C,S)
The output argument
metricis an n-by-1 numeric vector, where each element is the loss of the corresponding observation in the data processed by the incremental learning functions during a learning cycle.You specify the function name (here,
customMetric).Cis an n-by-K logical matrix with rows indicating the class to which the corresponding observation belongs, where K is the number of classes. The column order corresponds to the class order in theClassNamesproperty. CreateCby settingC(=p,q)1, if observationpqp0.Sis an n-by-K numeric matrix of predicted classification scores.Sis similar to theNegLossoutput ofpredict, where rows correspond to observations in the data and the column order corresponds to the class order in theClassNamesproperty.S(is the classification score of observationp,q)pq
To specify multiple custom metrics and assign a custom name to each, use a structure array. To specify a combination of built-in and custom metrics, use a cell vector.
updateMetrics and updateMetricsAndFit store
specified metrics in a table in the Metrics property. The data type of Metrics determines the
row names of the table.
Metrics Value Data Type | Description of Metrics Property Row Name | Example |
|---|---|---|
| String or character vector | Name of corresponding built-in metric | Row name for "classiferror" is
"ClassificationError" |
| Structure array | Field name | Row name for struct(Metric1=@customMetric1) is
"Metric1" |
| Function handle to function stored in a program file | Name of function | Row name for @customMetric is
"customMetric" |
| Anonymous function | CustomMetric_, where
Metrics | Row name for @(C,S)customMetric(C,S)... is
CustomMetric_1 |
For more details on performance metrics options, see Performance Metrics.
Example: Metrics=struct(Metric1=@customMetric1,Metric2=@customMetric2)
Example: Metrics={@customMetric1,@customMetric2,"classiferror",struct(Metric3=@customMetric3)}
Data Types: char | string | struct | cell | function_handle
Number of observations the incremental model must be fit to before it tracks
performance metrics in its Metrics property, specified as a
nonnegative integer. The incremental model is warm after incremental fitting functions
fit MetricsWarmupPeriod observations to the incremental
model.
For more details on performance metrics options, see Performance Metrics.
Example: MetricsWarmupPeriod=50
Data Types: single | double
Number of observations to use to compute window performance metrics, specified as a positive integer.
For more details on performance metrics options, see Performance Metrics.
Example: MetricsWindowSize=250
Data Types: single | double
Flag for updating the metrics of binary learners, specified as logical 0 (false) or 1 (true).
If the value is true, the software tracks the performance metrics
of binary learners using the Metrics property of the binary learners,
stored in the BinaryLearners property. For an example, see Configure Incremental Model to Track Performance Metrics for Model and Binary Learners.
Example: UpdateBinaryLearnerMetrics=true
Data Types: logical
Output Arguments
ECOC classification model for incremental learning, returned as an incrementalClassificationECOC model object.
IncrementalMdl is also configured to generate predictions given
new data (see predict).
To initialize IncrementalMdl for incremental learning,
incrementalLearner passes the values of the properties of
Mdl in this table to corresponding properties of
IncrementalMdl.
| Property | Description |
|---|---|
BinaryLearners | Trained binary learners, a cell array of model objects. The learners in
Mdl are traditionally trained binary learners, and the
learners in IncrementalMdl are binary learners for
incremental learning converted from the traditionally trained binary
learners. |
BinaryLoss | Binary learner loss function, a character vector. You can specify a
different value by using the BinaryLoss name-value
argument. |
ClassNames | Class labels for binary classification, a list of names |
CodingMatrix | Class assignment codes for the binary learners, a numeric matrix |
CodingName | Coding design name, a character vector |
NumPredictors | Number of predictors, a positive integer |
Prior | Prior class label distribution, a numeric vector |
Note that incrementalLearner does not use the
Cost property of Mdl because
incrementalClassificationECOC does not support it.
More About
Incremental learning, or online learning, is a branch of machine learning concerned with processing incoming data from a data stream, possibly given little to no knowledge of the distribution of the predictor variables, aspects of the prediction or objective function (including tuning parameter values), or whether the observations are labeled. Incremental learning differs from traditional machine learning, where enough labeled data is available to fit to a model, perform cross-validation to tune hyperparameters, and infer the predictor distribution.
Given incoming observations, an incremental learning model processes data in any of the following ways, but usually in this order:
Predict labels.
Measure the predictive performance.
Check for structural breaks or drift in the model.
Fit the model to the incoming observations.
For more details, see Incremental Learning Overview.
The classification error has the form
where:
wj is the weight for observation j. The software renormalizes the weights to sum to 1.
ej = 1 if the predicted class of observation j differs from its true class, and 0 otherwise.
In other words, the classification error is the proportion of observations misclassified by the classifier.
The binary loss is a function of the class and classification score that determines how well a binary learner classifies an observation into the class. The decoding scheme of an ECOC model specifies how the software aggregates the binary losses and determines the predicted class for each observation.
Assume the following:
mkj is element (k,j) of the coding design matrix M—that is, the code corresponding to class k of binary learner j. M is a K-by-B matrix, where K is the number of classes, and B is the number of binary learners.
sj is the score of binary learner j for an observation.
g is the binary loss function.
is the predicted class for the observation.
The software supports two decoding schemes:
Loss-based decoding [3] (
Decodingis"lossbased") — The predicted class of an observation corresponds to the class that produces the minimum average of the binary losses over all binary learners.Loss-weighted decoding [2] (
Decodingis"lossweighted") — The predicted class of an observation corresponds to the class that produces the minimum average of the binary losses over the binary learners for the corresponding class.The denominator corresponds to the number of binary learners for class k. [1] suggests that loss-weighted decoding improves classification accuracy by keeping loss values for all classes in the same dynamic range.
The predict, resubPredict, and
kfoldPredict functions return the negated value of the objective
function of argmin as the second output argument
(NegLoss) for each observation and class.
This table summarizes the supported binary loss functions, where yj is a class label for a particular binary learner (in the set {–1,1,0}), sj is the score for observation j, and g(yj,sj) is the binary loss function.
| Value | Description | Score Domain | g(yj,sj) |
|---|---|---|---|
"binodeviance" | Binomial deviance | (–∞,∞) | log[1 + exp(–2yjsj)]/[2log(2)] |
"exponential" | Exponential | (–∞,∞) | exp(–yjsj)/2 |
"hamming" | Hamming | [0,1] or (–∞,∞) | [1 – sign(yjsj)]/2 |
"hinge" | Hinge | (–∞,∞) | max(0,1 – yjsj)/2 |
"linear" | Linear | (–∞,∞) | (1 – yjsj)/2 |
"logit" | Logistic | (–∞,∞) | log[1 + exp(–yjsj)]/[2log(2)] |
"quadratic" | Quadratic | [0,1] | [1 – yj(2sj – 1)]2/2 |
The software normalizes binary losses so that the loss is 0.5 when yj = 0, and aggregates using the average of the binary learners [1].
Do not confuse the binary loss with the overall classification loss (specified by the
LossFun name-value argument of the loss and
predict object functions), which measures how well an ECOC classifier
performs as a whole.
Algorithms
The
updateMetricsandupdateMetricsAndFitfunctions track model performance metrics (Metrics) from new data only when the incremental model is warm (IsWarmproperty istrue).If you create an incremental model by using
incrementalLearnerandMetricsWarmupPeriodis 0 (default forincrementalLearner), the model is warm at creation.Otherwise, an incremental model becomes warm after
fitorupdateMetricsAndFitperforms both of these actions:Fit the incremental model to
MetricsWarmupPeriodobservations, which is the metrics warm-up period.Fit the incremental model to all expected classes (see the
MaxNumClassesandClassNamesarguments ofincrementalClassificationECOC).
The
Metricsproperty of the incremental model stores two forms of each performance metric as variables (columns) of a table,CumulativeandWindow, with individual metrics in rows. When the incremental model is warm,updateMetricsandupdateMetricsAndFitupdate the metrics at the following frequencies:Cumulative— The functions compute cumulative metrics since the start of model performance tracking. The functions update metrics every time you call the functions and base the calculation on the entire supplied data set.Window— The functions compute metrics based on all observations within a window determined byMetricsWindowSize, which also determines the frequency at which the software updatesWindowmetrics. For example, ifMetricsWindowSizeis 20, the functions compute metrics based on the last 20 observations in the supplied data (X((end – 20 + 1):end,:)andY((end – 20 + 1):end)).Incremental functions that track performance metrics within a window use the following process:
Store a buffer of length
MetricsWindowSizefor each specified metric, and store a buffer of observation weights.Populate elements of the metrics buffer with the model performance based on batches of incoming observations, and store corresponding observation weights in the weights buffer.
When the buffer is full, overwrite the
Windowfield of theMetricsproperty with the weighted average performance in the metrics window. If the buffer overfills when the function processes a batch of observations, the latest incomingMetricsWindowSizeobservations enter the buffer, and the earliest observations are removed from the buffer. For example, supposeMetricsWindowSizeis 20, the metrics buffer has 10 values from a previously processed batch, and 15 values are incoming. To compose the length 20 window, the functions use the measurements from the 15 incoming observations and the latest 5 measurements from the previous batch.
The software omits an observation with a
NaNscore when computing theCumulativeandWindowperformance metric values.
References
[1] Allwein, E., R. Schapire, and Y. Singer. “Reducing multiclass to binary: A unifying approach for margin classifiers.” Journal of Machine Learning Research. Vol. 1, 2000, pp. 113–141.
[2] Escalera, S., O. Pujol, and P. Radeva. “On the decoding process in ternary error-correcting output codes.” IEEE Transactions on Pattern Analysis and Machine Intelligence. Vol. 32, Issue 7, 2010, pp. 120–134.
[3] Escalera, S., O. Pujol, and P. Radeva. “Separability of ternary codes for sparse designs of error-correcting output codes.” Pattern Recog. Lett. Vol. 30, Issue 3, 2009, pp. 285–297.
Version History
Introduced in R2022a
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)