Model System Algorithm
When incomplete system requirements and a developing system design prevent you from defining file management and model architecture upfront, you can still model fundamental system algorithms. By organizing the model into inputs, outputs, and systems, you create a general framework for model components as the model grows.
To show the first stage of a modeling workflow that begins with limited information, this example uses a simple mechanical system composed of a mass, spring, and damper.
This second-order differential equation characterizes the system.
In this equation:
is mass.
is the damping coefficient.
is the spring constant.
is acceleration.
is velocity.
is displacement.
is external force.
Solving for provides a form of this equation that maps more clearly to a Simulink® model.
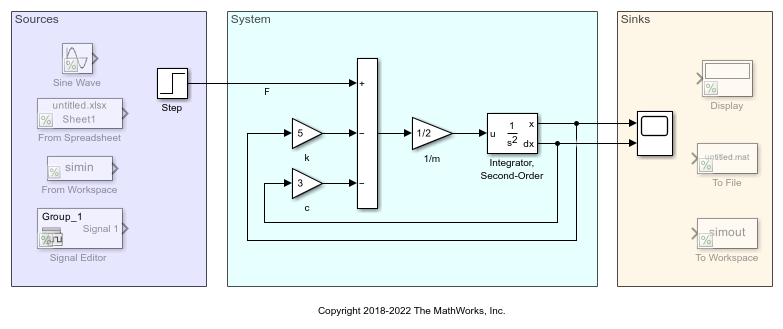
The model named BasicModelingSimpleSystem represents this equation.
mdl = "BasicModelingSimpleSystem";
open_system(mdl);
A Sum block computes the net force applied to the mass. The Gain block labeled 1/m computes the acceleration of the mass by multiplying the net force by . The Integrator, Second-Order block solves for the velocity and position of the mass.
The model organizes the blocks into three areas:
The area named
Sourcescontains system inputs.The area named
Systemcontains blocks that represent the system, or plant.The area named
Sinkscontains system outputs.
By organizing the model upfront, you create a general framework for model components as the model grows.
Because this example shows a model in the preliminary stages of development, the actual input force is unknown and can be represented by a variety of standard source blocks. The model uses a Step block connected as input to the system. Some alternative source blocks are shown but commented out. For example, you can use the From Spreadsheet block to load available empirical data.
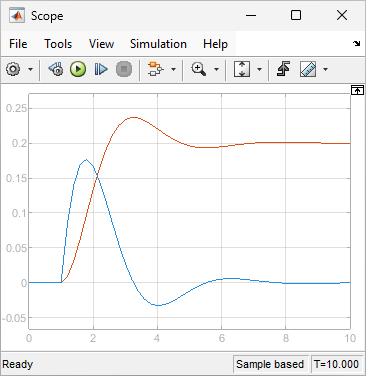
Similarly, a variety of sink blocks can accept the output displacement. To check whether simulation results meet expectations, the model uses a Scope block to visualize the signals.
sim(mdl);