Group Delay and Phase Delay

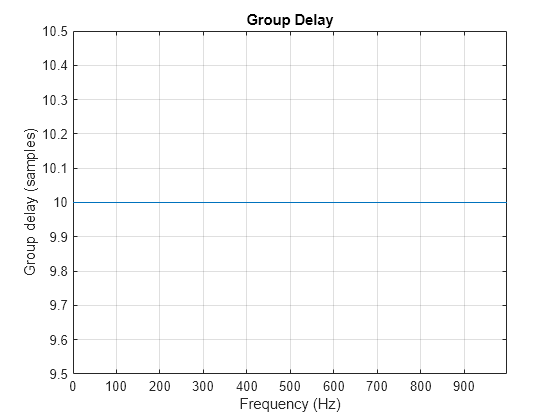
The group delay of a filter is a measure of the average time delay of the filter as a function of frequency. The group delay is defined as the negative first derivative of the filter's phase response. If the complex frequency response of a filter is $$H\left(e^{j\omega }\right)$$, then the group delay is

${\tau }_{\mathrm{g}}\left(\omega \right)=-\frac{\mathit{d}\theta \left(\omega \right)}{\mathit{d}\omega }$,

where $\theta \left(\omega \right)$ is the phase, or argument, of $$H\left(e^{j\omega }\right)$$. Use the grpdelay function to compute group delay of a filter. For example, verify that, for a linear-phase FIR filter, the group delay is one-half the filter order.

fs = 2000;
b = fir1(20,200/(fs/2));

islinphase(b)

ans = logical
   1

grpdelay(b,1,[],fs)

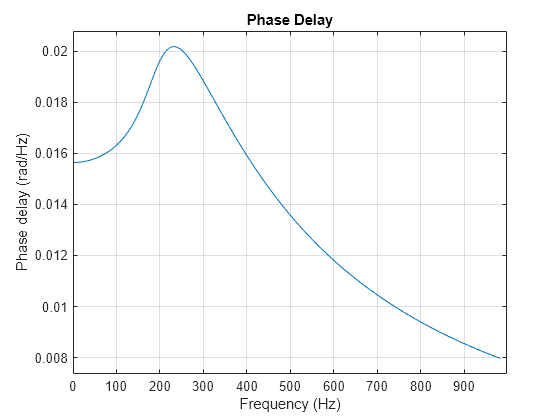
The phase delay of a filter is defined as the negative of the phase divided by the frequency:

$${\tau }_p\left(\omega \right)=-\frac{\theta \left(\omega \right)}{\omega }$$.

Use the phasedelay function to compute the phase delay of a filter. For the linear-phase FIR filter of the previous example, the phase delay is equal to the group delay.

phasedelay(b,1,[],fs)

Plot the group delay and the phase delay of a fifth-order Butterworth lowpass filter.

[b,a] = butter(5,200/(fs/2));

grpdelay(b,a,[],fs)

phasedelay(b,a,[],fs)