rpmtrack
Track and extract RPM profile from vibration signal
Syntax
Description
rpm = rpmtrack(x,fs,order,p)rpm from a vibration signal x
sampled at a rate fs.
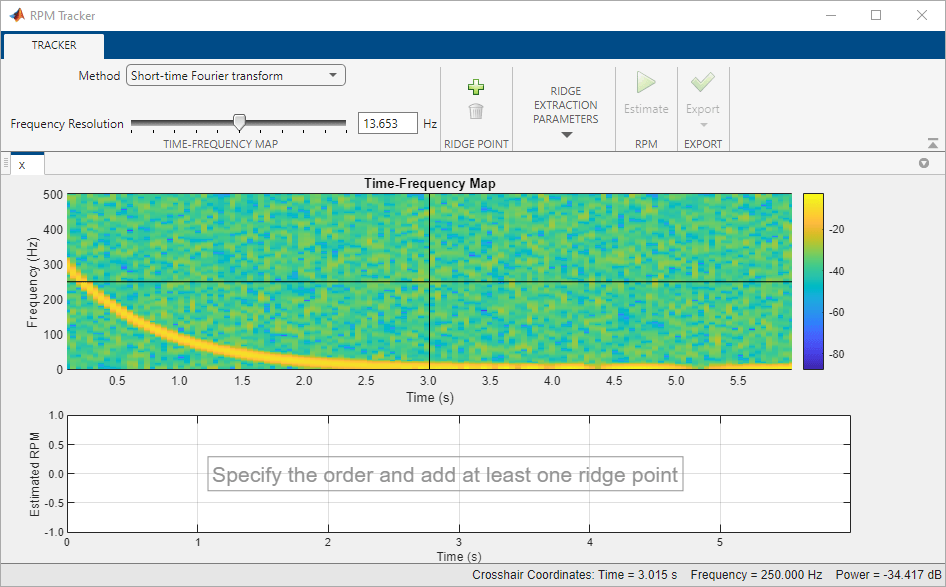
The two-column matrix p contains a set of points that lie
on a time-frequency ridge corresponding to a given order.
Each row of p specifies one coordinate pair. If you call
rpmtrack without specifying both
order and p, the function opens an
interactive plot that displays the time-frequency map and enables you to select
the points.
If you have a tachometer pulse signal, use tachorpm to extract
rpm directly.
rpm = rpmtrack(___,Name=Value)
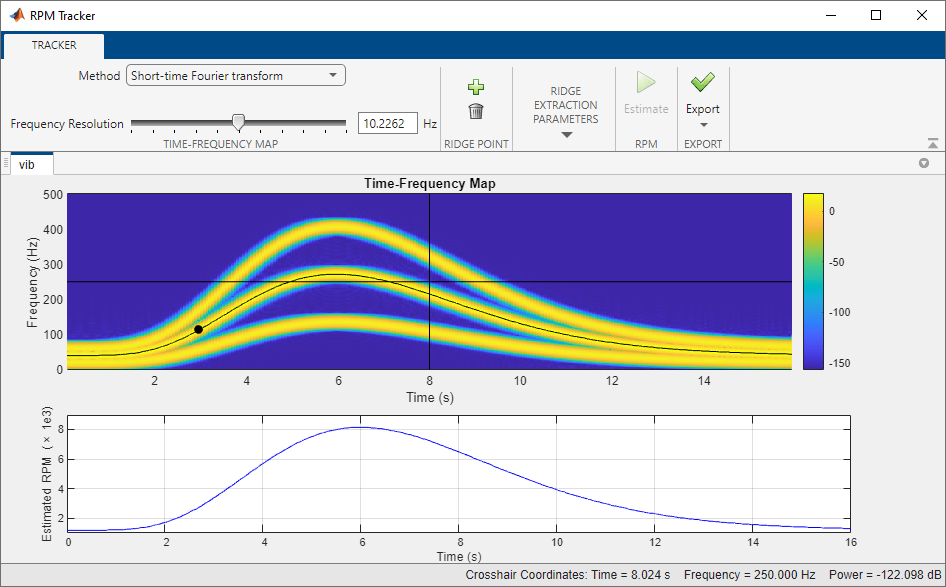
rpmtrack(___) with no output arguments plots
the power time-frequency map and the estimated RPM profile on an interactive
figure.
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Algorithms
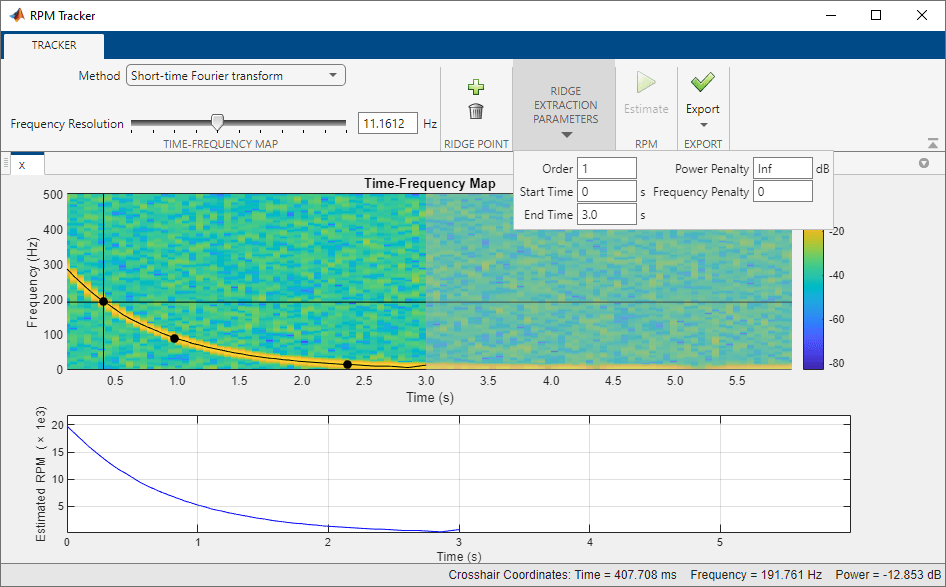
rpmtrack uses a two-step (coarse-fine) estimation method:
Compute a time-frequency map of
xand extract a time-frequency ridge based on a specified set of points on the ridge,p, theordercorresponding to that ridge, and the optional penalty parametersPowerPenaltyandFrequencyPenalty. The extracted ridge provides a coarse estimate of the RPM profile.Compute the order waveform corresponding to the extracted ridge using a Vold-Kalman filter and calculate a new time-frequency map from this waveform. The isolated order ridge from the new time-frequency map provides a fine estimate of the RPM profile.
References
[1] Urbanek, Jacek, Tomasz Barszcz, and Jerome Antoni. "A Two-Step Procedure for Estimation of Instantaneous Rotational Speed with Large Fluctuations." Mechanical Systems and Signal Processing. Vol. 38, 2013, pp. 96–102.
Extended Capabilities
Version History
Introduced in R2018a