Find Zeros, Poles, and Gains for CTLE from Transfer Function
This example shows how to use the CTLE Fitter app to configure a CTLE block from SerDes Toolbox™ in the SerDes Designer app or in Simulink®. You can use the CTLE Fitter app to fit zeros, poles, and gains from a transfer function to create a GPZ Matrix and then export to your workspace. The CTLE Fitter app finds the GPZ Matrix by performing a fit comparison to a transfer function using the rational (RF Toolbox) function from RF Toolbox™.
Using CTLE Fitter App
You can open the CTLE Fitter app from SerDes Toolbox using any of the three workflows:
From the CTLE block in the SerDes Designer app.
From the CTLE block in the Simulink model.
From the MATLAB® command window in the standalone mode.
Configure CTLE Block in SerDes Designer App
This workflow creates a variable representing a GPZ Matrix in the base workspace that is referenced by the CTLE block GPZ properties field in the SerDes Designer App. The steps are:
Add a CTLE block and click the button Launch CTLE Fitter App.
Import a CTLE frequency response. There can also be multiple responses in your data file.
Adjust preprocess options for your transfer function data.
Configure parameters of the
rationalfunction from RF Toolbox to optimize the fit to the transfer function.Visualize the fit response within the CTLE Fitter app using plots provided for magnitude response and pulse response.
Close the CTLE Fitter app and continue with your session in the SerDes Designer app.
Simulink SerDes Model with CTLE block
This workflow creates a variable representing a GPZ Matrix in the model workspace and references this in the CTLE block mask GPZ field. The steps are:
Open the CTLE block mask and click the button Launch CTLE Fitter App.
Import a CTLE frequency response.
Adjust preprocess options for your transfer function data.
Configure parameters of the
rationalfunction from RF Toolbox to optimize the fit to the transfer function.Visualize the fit response within the CTLE Fitter app using plots provided for magnitude response and pulse response.
Close the CTLE Fitter app and continue with your session in Simulink.
Standalone Mode
This workflow creates a variable in the base workspace representing a GPZ Matrix. The steps are:
Launch the app with the MATLAB command
ctlefitter.Import a CTLE frequency response.
Adjust preprocess options for your transfer function data.
Configure parameters of the
rationalfunction from RF Toolbox to optimize the fit to the transfer function.Visualize the fit response within the CTLE Fitter app using plots provided for magnitude response and pulse response.
You have the option to both export a script and save a
GPZ Matrixto the base workspace.Close the CTLE Fitter app and continue with your session in MATLAB
Configure CTLE Block in the SerDes Designer App
Launch the SerDes Designer app. Place a CTLE block after the analog model of the receiver. Then in the Block Parameters panel, click the button Launch CTLE Fitter App to launch the CTLE Fitter app.
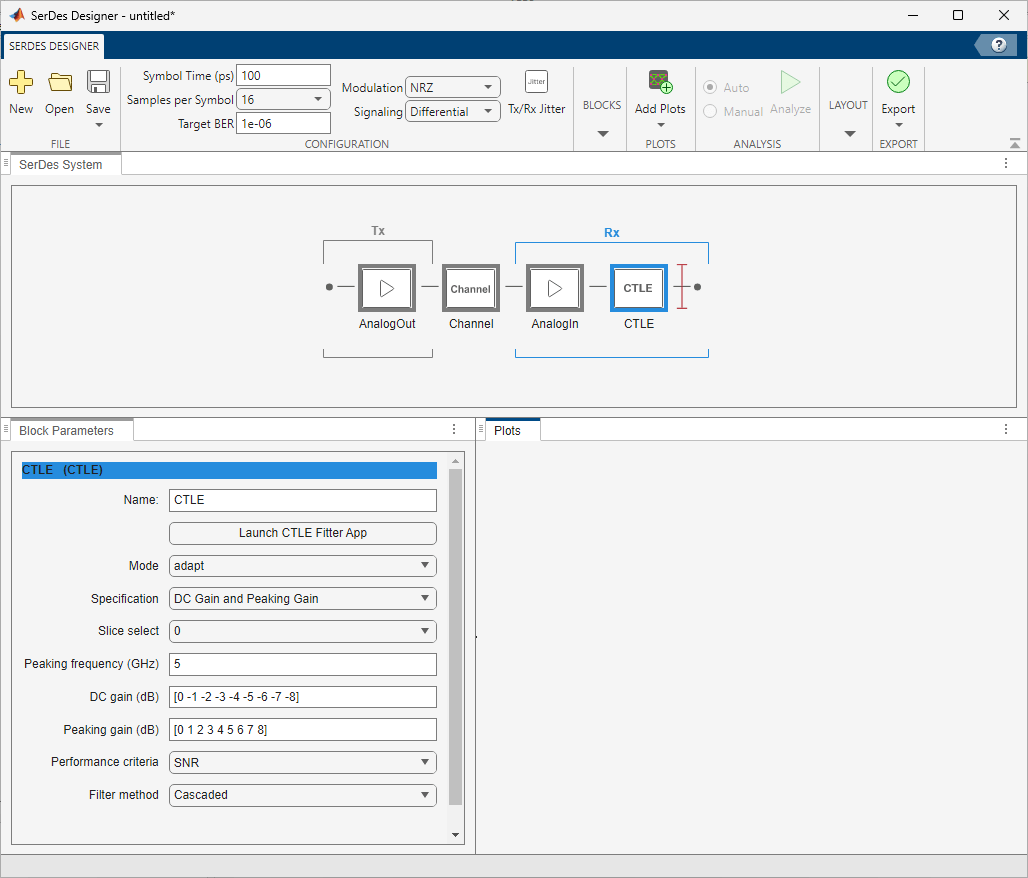
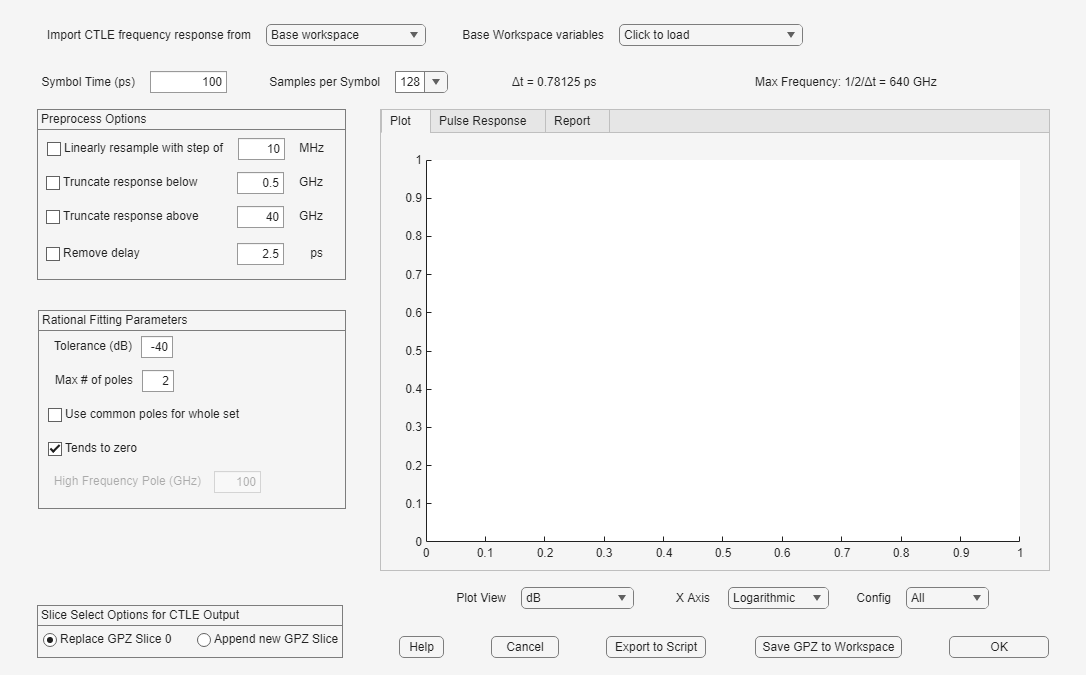
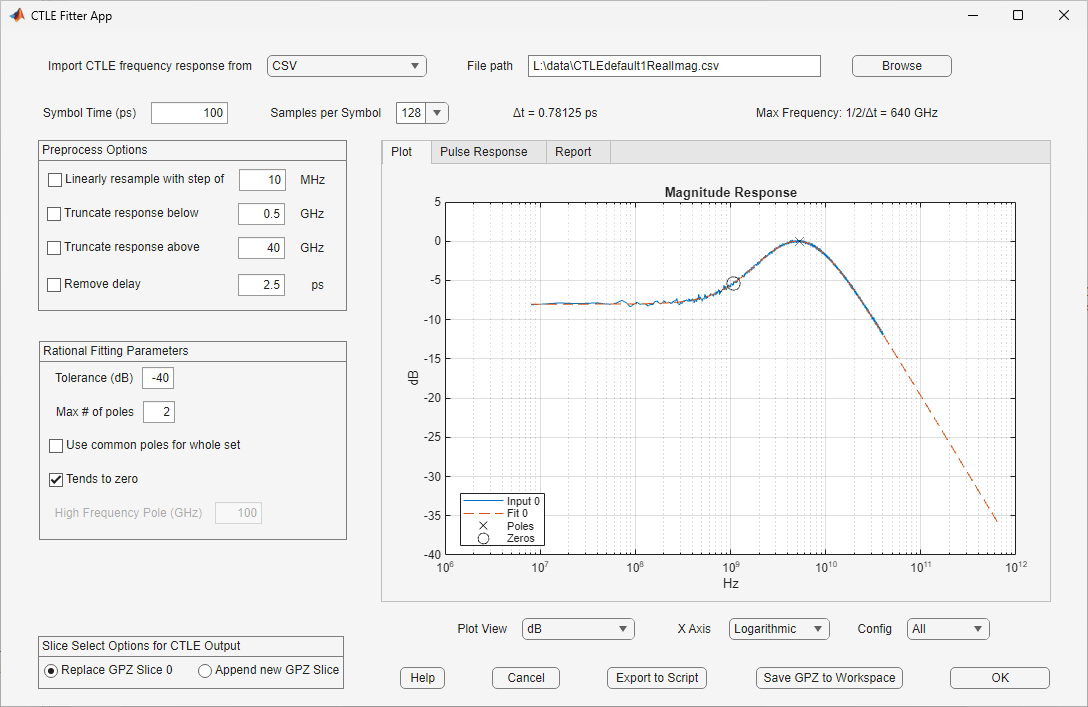
Import One or More CTLE Frequency Responses
The CTLE Fitter app opens with some default values. To import a file containing one or more CTLE frequency responses:
Download the file
CTLEdefault1RealImag.csvattached with this example to a location in your computer.Select the Import CTLE frequency response from parameter to
CSV, and browse to the location where you saved the CSV file.The app loads the file and automatically updates the figure shown on the Plot tab:

Adjust Preprocess Options
You can adjust many Preprocess Options in the app. For example, you can truncate the data set from the transfer function used by the Fit to a cutoff frequency of 13 GHz. To do so, select the Truncate response above parameter at set the value to 13 GHz, then click OK.

You can also adjust:
Linearly resample with step size in MHz
Truncate response below a specified frequency in GHz
Truncate response above a specified frequency in GHz
Remove delay in picoseconds
Configure Rational Fitting Parameters
You can configure the way the MATLAB function rational (RF Toolbox) determines a fit by adjusting the following:
Error tolerance (dB)
Maximum number of poles
Use common poles for whole set
Enable or disable "tends to zero"
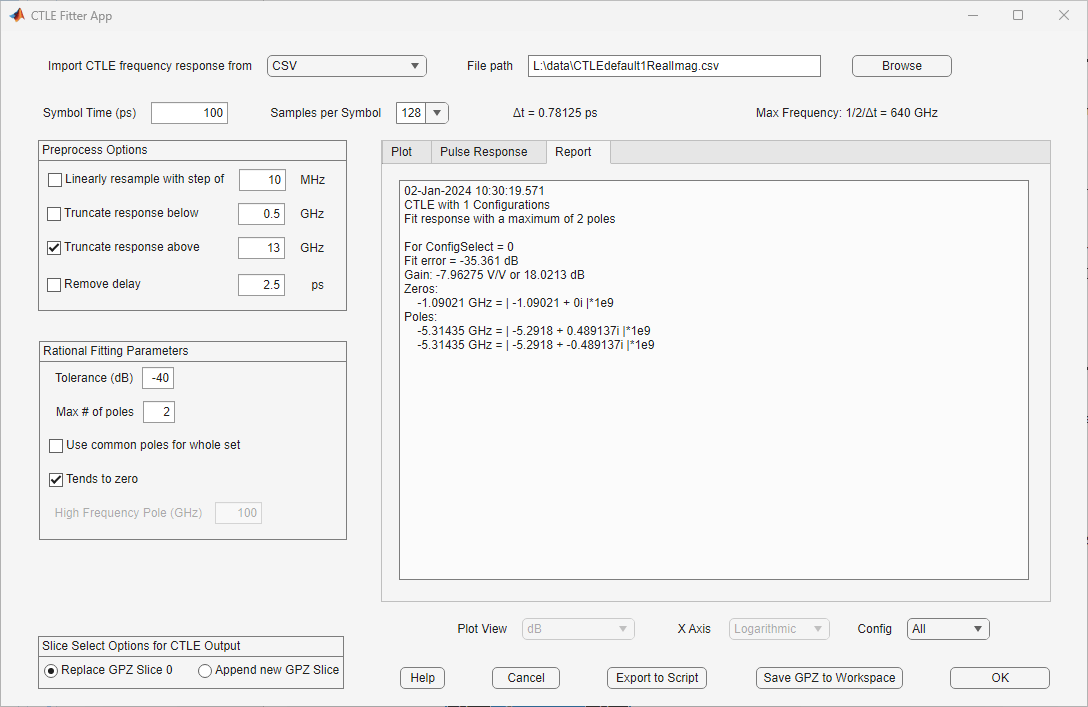
Report on Rational Fit Results
You can view the statistical parameters of the fit reported by the MATLAB function rational on the Report tab:
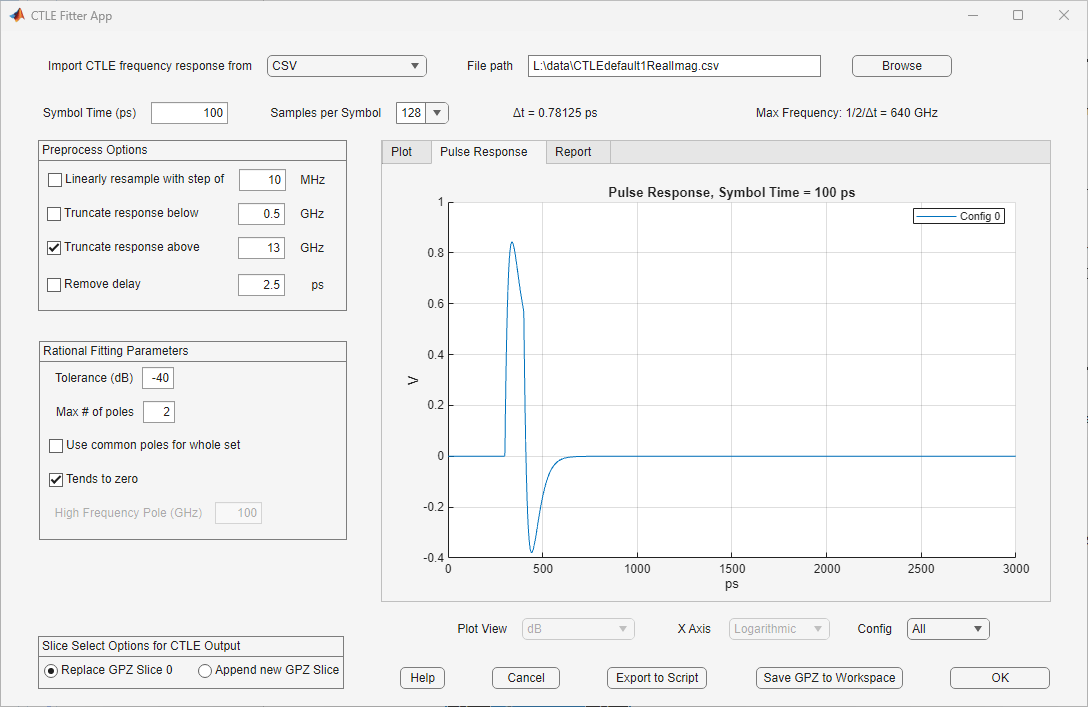
Pulse Response
You can view the pulse response on the Pulse Response tab:
Export a GPZ Matrix for CTLE Block
You can export the GPZ Matrix to the base workspace by clicking on the button Save GPZ to Workspace.

Note: If you have previously exported a GPZ Matrix, the name will automatically increment. For example, if gpz01 already exists in the workspace it would be automatically named gpz02 and added to your workspace.
Export Script from CTLE Fitter App to Base Workspace
You can also export a script from the CTLE Fitter app to the base workspace by clicking the Export to Script button. You can see example output below.
Note: If you use a different data file with your custom CTLE specifications, the example script may be different.
% ------------------------------------ % MATLAB script for CTLE Fitter. 02-Jan-2024 % ------------------------------------ %Read in file: fn = 'L:\data\CTLEdefault1RealImag.csv'; [f,H]=ctlefit.readcsv(fn); SymbolTime = 1e-10; %Initialize ctleit object obj = ctlefit(... 'f',f,... 'H',H,... 'SampleInterval',7.8125e-13,... 'MaxNumberOfPoles',2,... 'ErrorTolerance',-40,... 'TendsToZero',1,... 'UseCommonPoles',0,... 'PaddedPole',1e+11); %Preprocess transfer function waveform df = 1e+07; %resample(obj,df); fcut1 = 5e+08; %truncateBelow(obj,fcut1); fcut2 = 1.3e+10; truncateAbove(obj,fcut2); delay = 2.5e-12; %removeDelay(obj,delay); %Get GPZ matrix gpz = obj.GPZ; %Visualize and create report %TFView (Transfer function view) can be 'dB', 'Phase', 'Real/Imag', %'Phase Delay', 'Group Delay'. TFView = 'dB'; %ConfigSelect (CTLE Configuration Select) can be - 'All', 'Worst fit', 0 to %N-1, where N is the number of configurations. ConfigSelect = 'All'; %AxisStyle can be 'semilogx', 'plot', 'semilogy' or 'loglog'. AxisStyle = 'semilogx'; figure, plot(obj,TFView,ConfigSelect,AxisStyle)

figure, plotPulse(obj,ConfigSelect,SymbolTime)

figure, plotError(obj,ConfigSelect)

figure, plotFitMetric(obj)
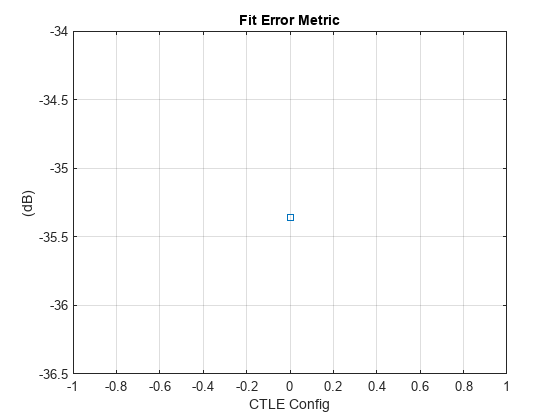
figure, plotPoleZero(obj,ConfigSelect,SymbolTime)
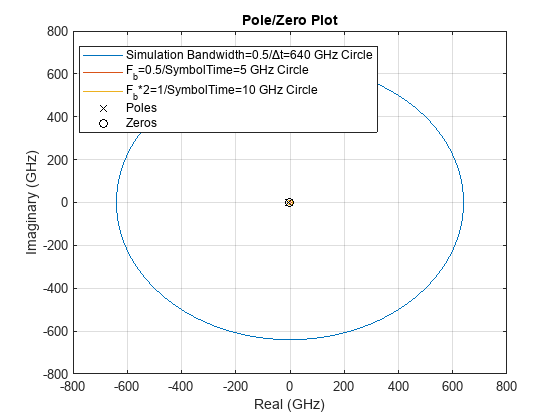
%report(obj,'All');Simulink SerDes Model with CTLE block
You can configure a Simulink SerDes Model with a CTLE block in a similar way.
Double click the CTLE block to open the Block Paramters dialog box, the click the Launce CTLE Fitter App button to open the CTLE Fitter app. Follow the same steps outlined in the section Configure CTLE Block in the SerDes Designer App to configure the CTLE Fitter app. Save the GPZ matrix to the base workspace, then click OK to close the app. The CLTE block is automatically updated to use the GPZ matrix you just created.
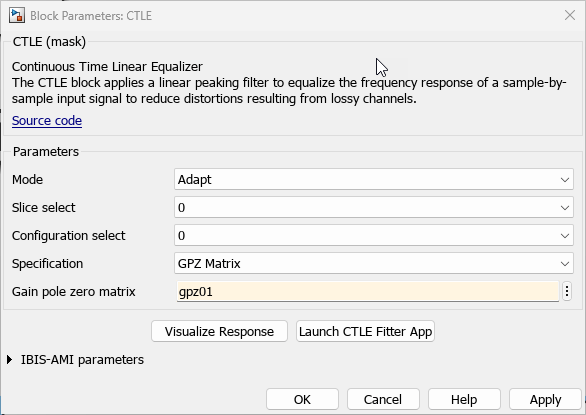
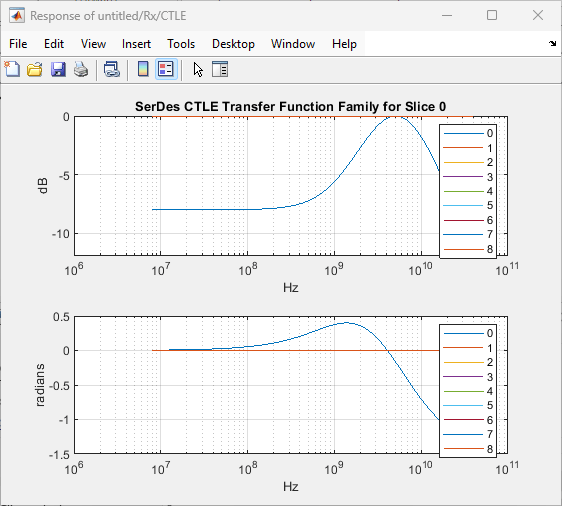
You can confirm the transfer function represented by the GPZ Matrix has a reasonable magnitude and phase response by clicking the Visualize Response button. These plots are also available in the SerDes Designer app workflow, and further detailed plots are provided as part of the exported script template.
Standalone Mode
Open the CTLE fitter app from the MATLAB command window:
ctlefitter;
You can follow the same steps outlined in the section Configure CTLE Block in the SerDes Designer App to configure the CTLE Fitter app and export a GPZ Matrix to the base workspace in your MATLAB session.
Once you browse to and open a file containing one or more CTLE filter responses, the app automatically updates the figure shown on the Plot tab:
See Also
SerDes Designer | CTLE | serdes.CTLE | rational (RF Toolbox)