Train DDPG Agent with Pretrained Actor Network

This example shows how to train a deep deterministic policy gradient (DDPG) agent for lane keeping assist (LKA) in Simulink. To make training more efficient, the actor of the DDPG agent is initialized with a deep neural network that was previously trained using supervised learning. This actor trained is trained in the Imitate MPC Controller for Lane Keeping Assist example.

For more information on DDPG agents, see Deep Deterministic Policy Gradient (DDPG) Agents.

Simulink Model

The training goal for the lane-keeping application is to keep the ego vehicle traveling along the centerline of the a lane by adjusting the front steering angle. This example uses the same ego vehicle dynamics and sensor dynamics as the Train DQN Agent for Lane Keeping Assist example.

m = 1575;   % total vehicle mass (kg)
Iz = 2875;  % yaw moment of inertia (mNs^2)
lf = 1.2;   % longitudinal distance from center of gravity to front tires (m)
lr = 1.6;   % longitudinal distance from center of gravity to rear tires (m)
Cf = 19000; % cornering stiffness of front tires (N/rad)
Cr = 33000; % cornering stiffness of rear tires (N/rad)
Vx = 15;    % longitudinal velocity (m/s)

Define the sample time, Ts, and simulation duration, T, in seconds.

Ts = 0.1;
T = 15;

The output of the LKA system is the front steering angle of the ego vehicle. Considering the physical limitations of the ego vehicle, constrain its steering angle to the range [-60,60] degrees. Specify the constraints in radians.

u_min = -1.04;
u_max = 1.04;

Define the curvature of the road as a constant 0.001($$m^{-1}$$).

rho = 0.001;

Set initial values for the lateral deviation (e1_initial) and the relative yaw angle (e2_initial). During training, these initial conditions are set to random values for each training episode.

e1_initial = 0.2;
e2_initial = -0.1;

Open the model.

mdl = 'rlActorLKAMdl';
open_system(mdl)

Define the path to the RL Agent block within the model.

agentblk = [mdl '/RL Agent'];

Create Environment

Create a reinforcement learning environment interface for the ego vehicle. To do so, first define the observation and action specifications. These observations and actions are the same as the features for supervised learning used in Imitate MPC Controller for Lane Keeping Assist.

The six observations for the environment are the lateral velocity ${\mathit{v}}_{\mathit{y}}$, yaw rate $$\underset{}{\overset{\dot{}}{\psi }}$$, lateral deviation ${\mathit{e}}_1$, relative yaw angle ${\mathit{e}}_2$, steering angle at previous step ${\mathit{u}}_0$, and curvature $\rho$.

observationInfo = rlNumericSpec([6 1],...
    LowerLimit=-inf*ones(6,1), ...
    UpperLimit= inf*ones(6,1))

observationInfo = 
  rlNumericSpec with properties:

     LowerLimit: [6x1 double]
     UpperLimit: [6x1 double]
           Name: [0x0 string]
    Description: [0x0 string]
      Dimension: [6 1]
       DataType: "double"

observationInfo.Name = "observations";

The action for the environment is the front steering angle. Specify the steering angle constraints when creating the action specification object.

actionInfo = rlNumericSpec([1 1], ...
    LowerLimit=u_min, ...
    UpperLimit=u_max);
actionInfo.Name = "steering";

In the model, the Signal Processing for LKA block creates the observation vector signal, computes the reward function, and calculates the stop signal.

The reward ${\mathit{r}}_{\mathit{t}}$, provided at every time step $\mathit{t}$, is as follows, where $\mathit{u}$ is the control input from the previous time step $\mathit{t}-1$.

$$r_t=-(10e_1^2+5e_2^2+2u^2+5{\underset{}{\overset{\dot{}}{e}}}_1^2+5{\underset{}{\overset{\dot{}}{e}}}_2^2)$$

The simulation stops when $$|e_1|>1$$.

Create the reinforcement learning environment.

env = rlSimulinkEnv(mdl,agentblk, ...
    observationInfo,actionInfo);

To define the initial condition for lateral deviation and relative yaw angle, specify an environment reset function using an anonymous function handle. The localResetFcn function, which is defined at the end of the example, sets the initial lateral deviation and relative yaw angle to random values.

env.ResetFcn = @(in)localResetFcn(in);

Fix the random generator seed for reproducibility.

rng(0)

Create DDPG Agent

A DDPG agent approximates the long-term reward given observations and actions using a critic value function representation. To create the critic, first create a deep neural network with two inputs, the state and action, and one output. For more information on creating a deep neural network value function representation, see Create Policies and Value Functions.

[critic,criticOptions] = createLaneKeepingCritic( ...
    observationInfo,actionInfo);

A DDPG agent decides which action to take given observations using an actor representation. To create the actor, first create a deep neural network with one input (the observation) and one output (the action).

[actor,actorOptions] = createLaneKeepingActor( ...
    observationInfo,actionInfo);

These initial actor and critic networks have random initial parameter values.

To create the DDPG agent, first specify the DDPG agent options.

agentOptions = rlDDPGAgentOptions(...
    SampleTime=Ts,...
    ActorOptimizerOptions=actorOptions,...
    CriticOptimizerOptions=criticOptions,...
    ExperienceBufferLength=1e6);
agentOptions.NoiseOptions.Variance = 0.3;
agentOptions.NoiseOptions.VarianceDecayRate = 1e-5;

Create the DDPG agent using the specified actor representation, critic representation, and agent options. For more information, see rlDDPGAgent.

agent = rlDDPGAgent(actor,critic,agentOptions);

Train Agent

As a baseline, train the agent with an actor that has random initial parameters. To train the agent, first specify the training options. For this example, use the following options.

• Run training for at most 50000 episodes, with each episode lasting at most 150 time steps.

• Display the training progress in the Episode Manager dialog box.

• Stop training when the episode reward reaches –1.

• Save a copy of the agent for each episode where the cumulative reward is greater than –2.5.

For more information, see rlTrainingOptions.

maxepisodes = 50000;
maxsteps = T/Ts;
trainingOpts = rlTrainingOptions(...
    MaxEpisodes=maxepisodes,...
    MaxStepsPerEpisode=maxsteps,...
    Verbose=false,...
    Plots="training-progress",...
    StopTrainingCriteria="EpisodeReward",...
    StopTrainingValue=-1,...
    SaveAgentCriteria="EpisodeReward",...
    SaveAgentValue=-2.5);

Train the agent using the train function. Training is a computationally intensive process that takes several hours to complete. To save time while running this example, load a pretrained agent by setting doTraining to false. To train the agent yourself, set doTraining to true.

doTraining = false;

if doTraining    
    % Train the agent.
    trainingStats = train(agent,env,trainingOpts);
else
    % Load pretrained agent for the example.
    load('ddpgFromScratch.mat');
end

Train Agent with Pretrained Actor

You can set the actor network of your agent to a deep neural network that has been previously trained. For this example, use the deep neural network from the Imitate MPC Controller for Lane Keeping Assist example. This network was trained to imitate a model predictive controller using supervised learning.

Load the pretrained actor network.

load('imitateMPCNetActorObj.mat','imitateMPCNetObj'); 

Create an actor representation using the pretrained actor.

supervisedActor = rlContinuousDeterministicActor( ...
    imitateMPCNetObj, ...
    observationInfo, ...
    actionInfo);

Check that the network used by supervisedActor is the same one that was loaded. To do so, evaluate both the network and the agent using the same random input observation.

testData = rand(6,1);

Evaluate the deep neural network.

predictImNN = predict(imitateMPCNetObj,testData');

Evaluate the actor.

evaluateRLRep = getAction(supervisedActor,{testData});

Compare the results.

error = evaluateRLRep{:} - predictImNN

error = single
    4.4703e-08

Create a DDPG agent using the pretrained actor.

agent = rlDDPGAgent(supervisedActor,critic,agentOptions);

Reduce the maximum number of training episodes and train the agent using the train function. To save time while running this example, load a pretrained agent by setting doTraining to false. To train the agent yourself, set doTraining to true.

trainingOpts.MaxEpisodes = 5000;
doTraining = false;

if doTraining    
    % Train the agent.
    trainingStats = train(agent,env,trainingOpts);
else
    % Load pretrained agent for the example.
    load('ddpgFromPretrained.mat');
end

By using the pretrained actor network, the training of the DDPG agent is more efficient. Both the total training time and the total number of training steps have improved by approximately 20%. Also, the number of episodes for the training to approach the neighborhood of the optimal result decreased from approximately 4500 to approximately 3500.

Simulate DDPG Agent

To validate the performance of the trained agent, uncomment the following two lines and simulate it within the environment. For more information on agent simulation, see rlSimulationOptions and sim.

% simOptions = rlSimulationOptions(MaxSteps=maxsteps);
% experience = sim(env,agent,simOptions);

To check the performance of the trained agent within the Simulink model, simulate the model using the previously defined initial conditions (e1_initial = 0.2 and e2_initial = -0.1).

sim(mdl)

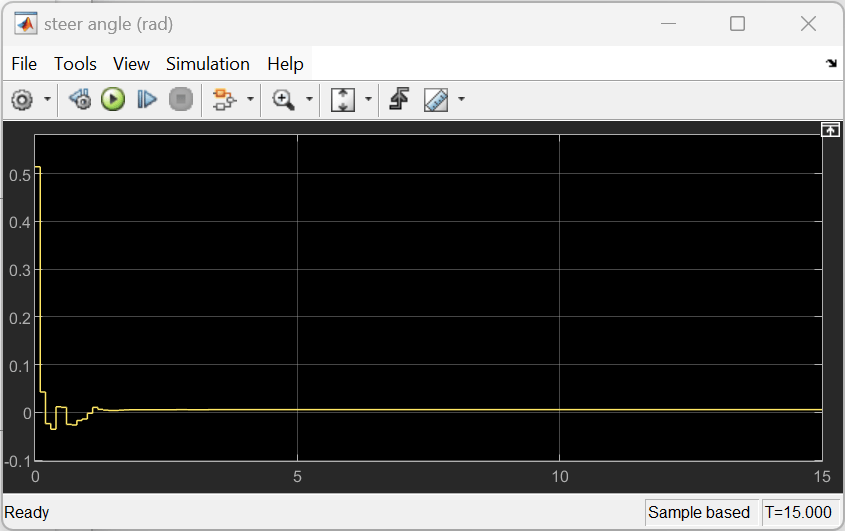
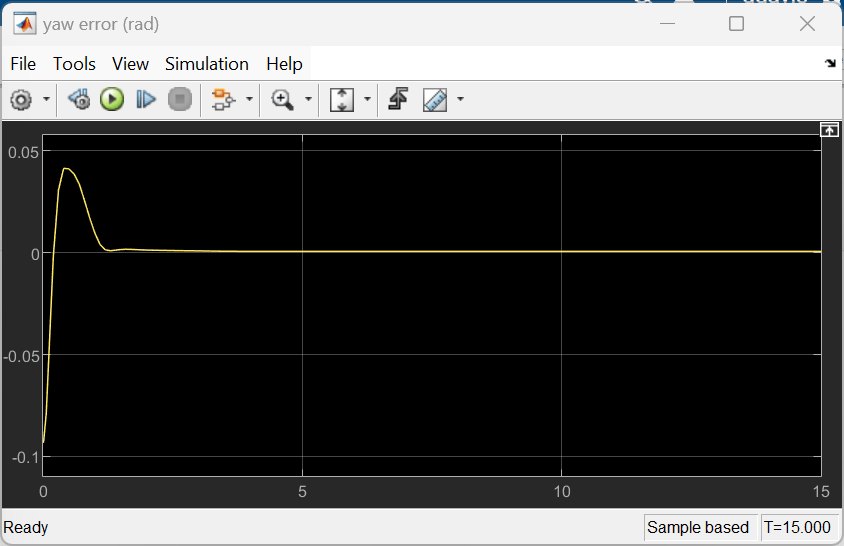
As shown below, the lateral error (middle plot) and relative yaw angle (bottom plot) are both driven to zero. The vehicle starts with a lateral deviation from the centerline (0.2 m) and a nonzero yaw angle error (-0.1 rad). The lane-keeping controller makes the ego vehicle travel along the centerline after around two seconds. The steering angle (top plot) shows that the controller reaches steady state after about two seconds.

Close the Simulink model without saving any changes.

bdclose(mdl)

Local Functions

function in = localResetFcn(in)
% Set random value for lateral deviation.
in = setVariable(in,'e1_initial', 0.5*(-1+2*rand));

% Set random value for relative yaw angle.
in = setVariable(in,'e2_initial', 0.1*(-1+2*rand));
end