Soft Actor-Critic (SAC) Agent
The soft actor-critic (SAC) algorithm is an off-policy actor-critic method for environments with discrete, continuous, and hybrid action-spaces. The SAC algorithm attempts to learn the stochastic policy that maximizes a combination of the policy value and its entropy. The policy entropy is a measure of policy uncertainty given the state. A higher entropy value promotes more exploration. Maximizing both the expected discounted cumulative long-term reward and the entropy balances exploration and exploitation of the environment. A soft actor-critic agent uses two critics to estimate the value of the optimal policy, while also featuring target critics and an experience buffer. SAC agents support offline training (training from saved data, without an environment). For more information on the different types of reinforcement learning agents, see Reinforcement Learning Agents.
In Reinforcement Learning Toolbox™, a soft actor-critic agent is implemented by an rlSACAgent object. This
implementation uses two Q-value function critics, which prevents overestimation of the value
function. Other implementations of the soft actor-critic algorithm use an additional value
function critic.
Soft actor-critic agents can be trained in environments with the following observation and action spaces.
| Observation Space | Action Space |
|---|---|
| Discrete or continuous | Discrete, continuous or hybrid |
Note
Soft actor-critic agents with an hybrid action space do not support training with an evolutionary strategy. Also, they cannot be used to build model based agents. Finally, while you can train offline (from existing data) any SAC agent, only SAC agents with continuous action space support batch data regularizer options.
Soft actor-critic agents use the following actor and critic. In the most general case, for hybrid action spaces, the action A has a discrete part Ad and a continuous part Ac.
| Critics | Actor |
|---|---|
Q-value function critics
Q(S,A), which you create
using | Stochastic policy actor
π(A|S), which you create
using |
During training, a soft actor-critic agent:
Updates the actor and critic learnable parameters at regular intervals during learning.
Estimates the probability distribution of the action and randomly selects an action based on the distribution.
Updates an entropy weight term to reduce the difference between entropy and target entropy.
Stores past experience using a circular experience buffer. The agent updates the actor and critic using a mini-batch of experiences randomly sampled from the buffer.
If the UseExplorationPolicy option of the agent is set to
false, the action with maximum likelihood is always used in sim and generatePolicyFunction. As a result, the simulated agent and generated policy
behave deterministically.
If the UseExplorationPolicy is set to true, the
agent selects its actions by sampling its probability distribution. As a result, the policy is
stochastic and the agent explores its observation space.
Note
The UseExplorationPolicy option affects only simulation and
deployment; it does not affect training. When you train an agent using train, the agent
always uses its exploration policy independently of the value of this property.
Actor and Critics Used by the SAC Agent
To estimate the policy and value function, a soft actor-critic agent maintains the following function approximators.
Stochastic actor π(A|S;θ).
For continuous-only action spaces, the actor outputs a vector containing the mean and standard deviation of the Gaussian distribution for the continuous part of the action. Note the SAC algorithm bounds the continuous action selected from the actor.
For discrete-only action spaces, the actor outputs a vector containing the probabilities of each possible discrete action.
For hybrid action spaces, the actor outputs both these vectors.
Both distributions are parameterized in θ and conditional to the observation being S.
One or two Q-value (or vector Q-value) critics Qk(S,Ac;ϕk) — The critics, each with parameters ϕk, take observation S and the continuous part of the action Ac (if present) as inputs and return the corresponding value function (for continuous action spaces), or the value of each possible discrete action Ad (for discrete or hybrid action spaces). The value function is calculated including the entropy of the policy as well as its expected discounted cumulative long-term reward.
One or two target critics Qtk(S,Ac;ϕtk) — To improve the stability of the optimization, the agent periodically sets the target critic parameters ϕtk to the latest corresponding critic parameter values. The number of target critics matches the number of critics.
When you use two critics, Q1(S,Ac;ϕ1) and Q2(S,Ac;ϕ2), each critic can have different structures. When the critics have the same structure, they must have different initial parameter values.
Each critic Qk(S,Ac;ϕk) and corresponding target critic Qtk(S,Ac;ϕtk) must have the same structure and parameterization.
During training, the actor tunes the parameter values in θ to improve the policy. Similarly, during training, the critics tune their parameter values to improve their action-value function estimation. After training, the parameters remain at their tuned values in the actor and critic internal to the trained agent.
For more information on actors and critics, see Create Policies and Value Functions.
Continuous Action Generation
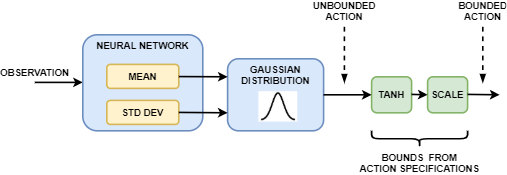
In a continuous action space soft actor-critic agent, the neural network in the actor takes the current observation and generates two outputs, one for the mean and the other for the standard deviation. To select an action, the actor randomly selects an unbounded action from this Gaussian distribution. If the soft actor-critic agent needs to generate bounded actions, the actor applies tanh and scaling operations to the action sampled from the Gaussian distribution.
During training, the agent uses the unbounded Gaussian distribution to calculate the entropy of the policy for the given observation.
Discrete Action Generation
In a discrete action space soft actor-critic agent, the actor takes the current observation and generates a categorical distribution, in which each possible action is associated with a probability. Since each action that belongs to the finite set is already assumed feasible, no bounding is needed.
During training, the agent uses the categorical distribution to calculate the entropy of the policy for the given observation.
Hybrid Action Generation
In a hybrid action space soft actor-critic agent, the actor takes the current observation and generates both a categorical and a Gaussian distribution, which are both used to calculate the entropy of the policy during training.
A discrete action is then sampled from the categorical distribution, and a continuous action is sampled from the Gaussian distribution. If needed, the continuous action is then also automatically bounded as for continuous action generation.
The discrete and continuous actions are then returned to the environment using two different action channels.
SAC Agent Creation
You can create and train soft actor-critic agents at the MATLAB® command line or using the Reinforcement Learning Designer app. For more information on creating agents using Reinforcement Learning Designer, see Create Agents Using Reinforcement Learning Designer.
At the command line, you can create a soft actor-critic agent with default actor and critic based on the observation and action specifications from the environment. To do so, perform the following steps.
Create observation specifications for your environment. If you already have an environment object, you can obtain these specifications using
getObservationInfo.Create action specifications for your environment. If you already have an environment object, you can obtain these specifications using
getActionInfo.If needed, specify the number of neurons in each learnable layer of the default network or whether to use a recurrent default network. To do so, create an agent initialization option object using
rlAgentInitializationOptions.If needed, specify agent options using an
rlSACAgentOptionsobject. Alternatively, you can skip this step and modify the agent options later using dot notation.Create the agent using
rlSACAgent.
Alternatively, you can create custom actor and critic objects and use them to create your agent. In this case, ensure that the input and output dimensions of the actor and critic match the corresponding action and observation specifications of the environment. To create an agent using your custom actor and critic objects, perform the following steps.
Create observation specifications for your environment. If you already have an environment object, you can obtain these specifications using
getObservationInfo.Create action specifications for your environment. If you already have an environment object, you can obtain these specifications using
getActionInfo.Create an approximation model for your actor. For continuous action spaces, this model must be a neural network object. For discrete action spaces, you also have the option of using a custom basis function with initial parameter values.
Create a stochastic actor using
rlContinuousGaussianActor(for continuous action spaces),rlDiscreteCategoricalActor(for discrete action spaces), orrlHybridStochasticActor(for hybrid action spaces). Use the model you created in the previous step as a first input argument. For soft actor-critic agents with continuous or hybrid action spaces, the actor network must not contain atanhLayerandscalingLayeras last two layers in the output path for the mean values, since the scaling already occurs automatically. However, to ensure that the standard deviation values are not negative, the actor network must contain areluLayeras the last layer in the output path for the standard deviation values.Create an approximation model for your critic. You can use a custom basis function with initial parameter values, or a neural network object. The inputs and outputs of the model you create depend on the type of critic you use in the next step.
Create one or two critics using
rlQValueFunction(for continuous action spaces) or usingrlVectorQValueFunction(for hybrid or discrete action spaces). Use the model you created in the previous step as a first input argument. For hybrid action spaces, the critics must take as inputs both the observation and the continuous action. If the critics have the same structure, they must have different initial parameter values.Specify agent options using an
rlSACAgentOptionsobject. Alternatively, you can skip this step and modify the agent options later using dot notation.Create the agent using
rlSACAgent.
For more information on creating actors and critics for function approximation, see Create Policies and Value Functions.
SAC Training Algorithm
The soft actor-critic agent uses the following training algorithm, in which it
periodically updates the actor and critic models and entropy weight. To configure the
training algorithm, specify options using an rlSACAgentOptions object.
Here, K = 2 is the number of critics and k is the critic
index.
Initialize each critic Qk(S,A;ϕk) with random parameter values ϕk, and initialize each target critic with the same random parameter values, .
Initialize the actor π(A|S;θ) with random parameter values θ.
Perform a warm start by taking a sequence of actions following the initial random policy in π(A|S).
At the beginning of each episode, get the initial observation from the environment.
For the current observation S, select the action A (with its continuous part bounded) using the policy in π(A|S;θ).
Execute action A. Observe the reward R and the next observation S'.
Store the experience (S,A,R,S') in the experience buffer.
To specify the size of the experience buffer, use the
ExperienceBufferLengthoption in the agentrlSACAgentOptionsobject. To specify the number of warm up actions, use theNumWarmStartStepsoption.After the warm start procedure, for each training time step:
Execute the four operations described in the warm start procedure.
Every DC time steps (to specify DC use the
LearningFrequencyoption), perform the following two operations forNumEpochtimes:Using all the collected experiences, create at most B different mini-batches. To specify B, use the
MaxMiniBatchPerEpochoption. Each mini-batch contains M different (typically nonconsecutive) experiences (Si,Ai,Ri,S'i) that are randomly sampled from the experience buffer (each experience can only be part of one mini-batch). To specify M, use theMiniBatchSizeoption.If the agent contains recurrent neural networks, each mini-batch contains M different sequences. Each sequence contains K consecutive experiences (starting from a randomly sampled experience). To specify K, use the
SequenceLengthoption.For each (randomly selected) mini-batch, perform the learning operations described in Mini-Batch Learning Operations.
When
LearningFrequencyis the default value of -1, the creation of the minibatches (described in point a) and the learning operations (described in point b) are executed after each episode is finished.
Mini-Batch Learning Operations
Operations performed for each mini-batch.
Update the parameters of each critic by minimizing the loss Lk across all sampled experiences.
To specify the optimizer options used to minimize Lk, use the options contained in the
CriticOptimizerOptionsoption (which in turn contains anrlOptimizerOptionsobject).If the agent contains recurrent neural networks, each element of the sum over the batch elements is itself a sum over the time (sequence) dimension.
If S'i is a terminal state, the value function target yi is set equal to the experience reward Ri. Otherwise, the value function target is the sum of Ri, the minimum discounted future reward from the critics, and the weighted entropy. The following formulas show the value function target in discrete, continuous, and hybrid action spaces, respectively.
Here:
The superscripts d, c, and h indicate the quantity in the discrete, continuous, and hybrid cases, respectively. Nd is the number of possible discrete actions, and Adj indicates the jth action belonging to the discrete action set.
γ is the discount factor, which you specify in the
DiscountFactoroption.The last two terms of the target equation for the hybrid case, (or the last term in the other cases) represent the weighted policy entropy for the output of the actor when in state S. αd and αc are the entropy loss weights for the discrete and continuous action spaces, which you specify by setting the
EntropyWeightoption of the respectiveEntropyWeightOptionsproperty. To specify the other optimizer options used to tune one of the entropy term, use the other properties of theEntropyWeightOptionsagent option.
If you specify a value of
NumStepsToLookAheadequal to N, then the N-step return (which adds the rewards of the following N steps and the discounted estimated value of the state that caused the N-th reward) is used to calculate the target yi.Every DA critic updates (to set DA, use the
PolicyUpdateFrequencyoption), perform the following two operations:Update the parameters of the actor by minimizing the following objective function across all sampled experiences. The following formulas show the objective function in discrete, continuous, and hybrid action spaces, respectively.
To specify the optimizer options used to minimize Jπ, use the options contained in the
ActorOptimizerOptionsoption (which in turn contains anrlOptimizerOptionsobject).If the agent contains recurrent neural networks, each element of the sum over the mini-batch elements is itself a sum over the time (sequence) dimension.
Update the entropy weights by minimizing the following loss functions. When the action space is discrete or continuous, only the respective entropy weight is minimized. When the action space is hybrid, both weights are updated by minimizing both functions.
Here, ℋd and ℋc are the target entropies for the discrete and continuous cases, which you specify in the
TargetEntropyproperty of the correspondingEntropyWeightOptions.TargetEntropyoption.
Every
TargetUpdateFrequencycritic updates, update the target critics depending on the target update method. For more information, see Target Update Methods.
Target Update Methods
Soft actor-critic agents update their target critic parameters using one of the following target update methods.
Smoothing — Update the target critic parameters using smoothing factor τ. To specify the smoothing factor, use the
TargetSmoothFactoroption.Periodic — Update the target critic parameters periodically without smoothing (
TargetSmoothFactor = 1). To specify the update period, use theTargetUpdateFrequencyparameter.Periodic smoothing — Update the target parameters periodically with smoothing.
To configure the target update method, set the
TargetUpdateFrequency and TargetSmoothFactor
parameters as shown in the following table.
| Update Method | TargetUpdateFrequency | TargetSmoothFactor |
|---|---|---|
| Smoothing (default) | 1 | Less than 1 |
| Periodic | Greater than 1 | 1 |
| Periodic smoothing | Greater than 1 | Less than 1 |
References
[1] Haarnoja, Tuomas, Aurick Zhou, Kristian Hartikainen, George Tucker, Sehoon Ha, Jie Tan, Vikash Kumar, et al. “Soft Actor-Critic Algorithms and Applications.” arXiv, January 29, 2019. https://arxiv.org/abs/1812.05905.
[2] Christodoulou, Petros. “Soft Actor-Critic for Discrete Action Settings.” arXiv, October 18, 2019.https://arxiv.org/abs/1910.07207.
[3] Delalleau, Olivier, Maxim Peter, Eloi Alonso, and Adrien Logut. “Discrete and Continuous Action Representation for Practical RL in Video Games.” arXiv, December 23, 2019. https://arxiv.org/abs/1912.11077
See Also
Functions
Objects
rlSACAgent|rlSACAgentOptions|rlQValueFunction|rlVectorQValueFunction|rlContinuousGaussianActor|rlHybridStochasticActor|rlDDPGAgent|rlTD3Agent|rlACAgent|rlPPOAgent