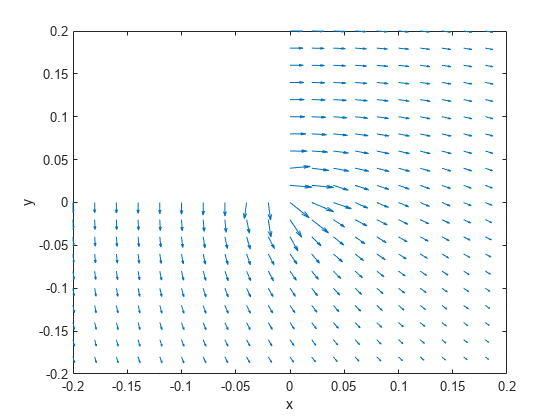
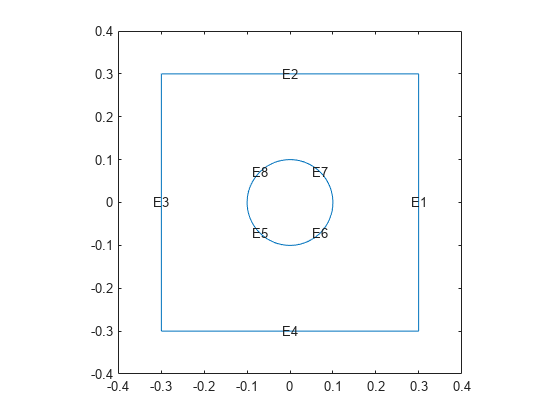
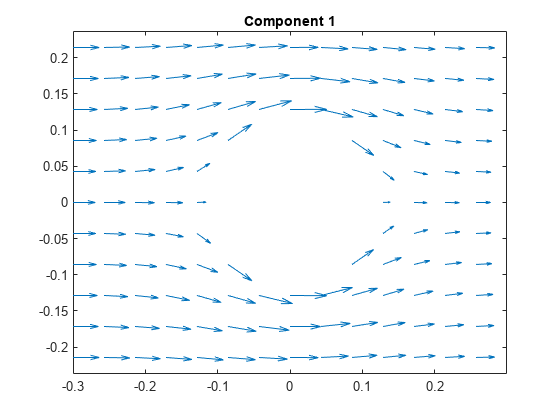
evaluateGradient
Evaluate gradients of PDE solutions at arbitrary points
Syntax
Description
[___] = evaluateGradient(
returns the interpolated values of the gradients at the points specified in
results,querypoints)querypoints.
[___] = evaluateGradient(___,
returns the interpolated values of the gradients for the system of equations for
equation indices (components) iU)iU. When solving a system of
elliptic PDEs, specify iU after the input arguments in any
of the previous syntaxes.
The first dimension of gradx, grady,
and, in 3-D case, gradz corresponds to query points. The
second dimension corresponds to equation indices iU.
[___] = evaluateGradient(___,
returns the interpolated values of the gradients for the time-dependent equation
or system of time-dependent equations at times iT)iT. When
evaluating gradient for a time-dependent PDE, specify iT
after the input arguments in any of the previous syntaxes. For a system of
time-dependent equations, specify both time indices iT and
equation indices (components) iU.
The first dimension of gradx, grady,
and, in 3-D case, gradz corresponds to query points. For a
single time-dependent PDE, the second dimension corresponds to time-steps
iT. For a system of time-dependent PDEs, the second
dimension corresponds to equation indices iU, and the third
dimension corresponds to time-steps iT.
Examples
Input Arguments
Output Arguments
Tips
The results object contains the solution and its gradient
calculated at the nodal points of the triangular or tetrahedral mesh. You can access the
solution and three components of the gradient at nodal points by using dot
notation.
interpolateSolution and evaluateGradient let
you interpolate the solution and its gradient to a custom grid, for example, specified
by meshgrid.
Version History
Introduced in R2016a
See Also
PDEModel | StationaryResults | TimeDependentResults | interpolateSolution | evaluateCGradient | quiver | quiver3 | contour