2-D Solution and Gradient Plots with MATLAB Functions
You can interpolate the solution and, if needed, its gradient in separate steps, and then plot the results by using MATLAB® functions, such as surf, mesh, quiver, and so on. For example, solve the same scalar elliptic problem on the L-shaped membrane with zero Dirichlet boundary conditions. Interpolate the solution and its gradient, and then plot the results.
Create the PDE model, 2-D geometry, and mesh. Specify boundary conditions and coefficients. Solve the PDE problem.
model = createpde; geometryFromEdges(model,@lshapeg); applyBoundaryCondition(model,"dirichlet", ... Edge=1:model.Geometry.NumEdges, ... u=0); c = 1; a = 0; f = 1; specifyCoefficients(model,m=0,d=0,c=c,a=a,f=f); generateMesh(model,Hmax=0.05); results = solvepde(model);
Interpolate the solution and its gradients to a dense grid from -1 to 1 in each direction.
v = linspace(-1,1,101); [X,Y] = meshgrid(v); querypoints = [X(:),Y(:)]'; uintrp = interpolateSolution(results,querypoints);
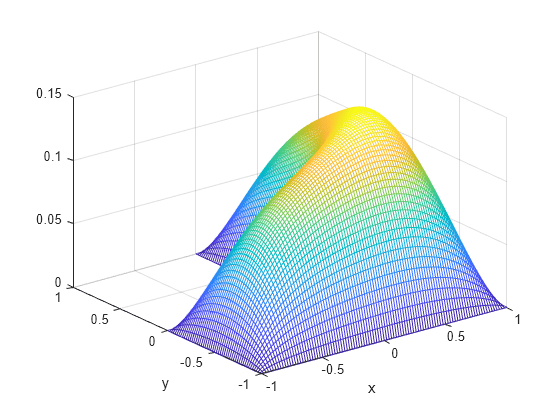
Plot the resulting solution on a mesh.
uintrp = reshape(uintrp,size(X)); mesh(X,Y,uintrp) xlabel("x") ylabel("y")
Interpolate gradients of the solution to the grid from -1 to 1 in each direction. Plot the result using quiver.
[gradx,grady] = evaluateGradient(results,querypoints); figure quiver(X(:),Y(:),gradx,grady) xlabel("x") ylabel("y")
Zoom in to see more details. For example, restrict the range to [-0.2,0.2] in each direction.
axis([-0.2 0.2 -0.2 0.2])

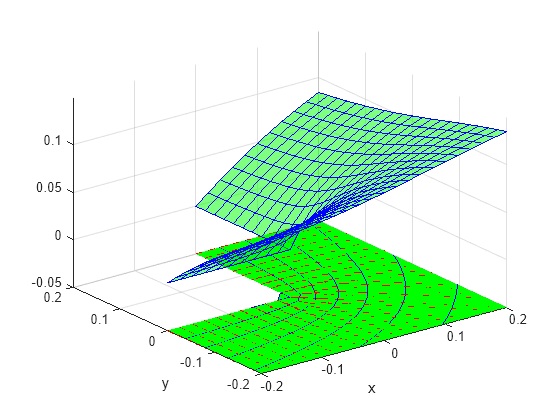
Plot the solution and the gradients on the same range.
figure h1 = meshc(X,Y,uintrp); set(h1,FaceColor="g",EdgeColor="b") xlabel("x") ylabel("y") alpha(0.5) hold on Z = -0.05*ones(size(X)); gradz = zeros(size(gradx)); h2 = quiver3(X(:),Y(:),Z(:),gradx,grady,gradz); set(h2,Color="r") axis([-0.2,0.2,-0.2,0.2])
Slice of the solution plot along the line x = y.
figure mesh(X,Y,uintrp) xlabel("x") ylabel("y") alpha(0.25) hold on z = linspace(0,0.15,101); Z = meshgrid(z); surf(X,X,Z') view([-20 -45 15]) colormap winter

Plot the interpolated solution along the line.
figure xq = v; yq = v; uintrp = interpolateSolution(results,xq,yq); plot3(xq,yq,uintrp) grid on xlabel("x") ylabel("y")
Interpolate gradients of the solution along the same line and add them to the solution plot.
[gradx,grady] = evaluateGradient(results,xq,yq);
gradx = reshape(gradx,size(xq));
grady = reshape(grady,size(yq));
hold on
quiver(xq,yq,gradx,grady)
view([-20 -45 75])