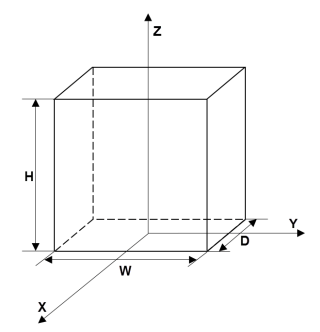
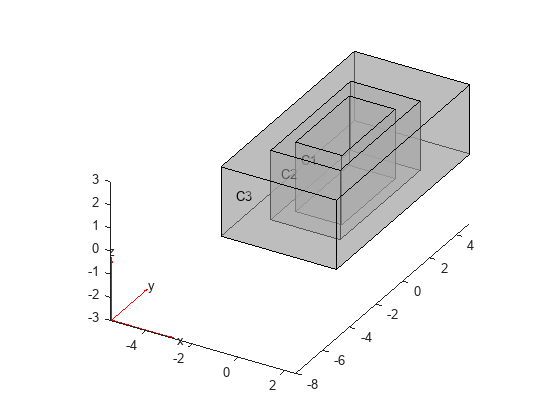
multicuboid
Create geometry formed by several cubic cells
Description
Examples
Input Arguments
Name-Value Arguments
Output Arguments
Limitations
multicuboidlets you create only geometries consisting of stacked or nested cuboids. For nested cuboids, the height must be the same for all cells in the geometry. For stacked cuboids, the width and depth must be the same for all cells in the geometry. Use theZOffsetargument to stack the cells on top of each other without overlapping them.multicuboiddoes not let you create nested cuboids of the same width and depth. The callmulticuboid(w,d,[h1,h2,...])is not supported.
Version History
Introduced in R2017a